Plantilla:Triángulos en la posición de Tales
De Wikipedia
| Revisión de 07:27 21 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 5: | Línea 5: | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo | {{Teorema_sin_demo | ||
| - | |titulo=Teorema | + | |titulo=Corolario |
| |enunciado=Dos [[triángulos]] son semejantes si y sólo si están en la posición de [[Tales]]. | |enunciado=Dos [[triángulos]] son semejantes si y sólo si están en la posición de [[Tales]]. | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Videos: Teorema de Tales}} | ||
| |celda2=<center>[[Imagen:triangulos_tales.png|220px|thumb|Triángulos en la posición de Thales]]</center> | |celda2=<center>[[Imagen:triangulos_tales.png|220px|thumb|Triángulos en la posición de Thales]]</center> | ||
| }} | }} | ||
| + | |||
| + | {{p}} | ||
Revisión actual
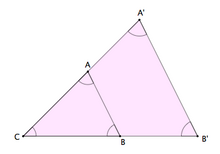
Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales   Tutorial 1 (7´18") Sinopsis:Teorema de Tales. Ejemplos.  Tutorial 2 (23´57") Sinopsis:Tutorial en el que se explica y trabaja el teorema de Tales y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
 Ejercicio 1 (3'28") Sinopsis:División de un segmento en partes proporcionales. Ejercicio 2 (2'43") Sinopsis:Dibujo y cálculo del 4º proporcional a tres segmentos dados. Ejercicio 3 (2'51") Sinopsis:Cálculo y dibujo del 3º proporcional a dos segmentos dados.  Ejercicio 4 (2´29") Sinopsis: Ejercicio de aplicación del primer teorema de Tales. Ejercicio 5 (7´19") Sinopsis: Ejercicio de aplicación del primer teorema de Thales.  Tutorial (3´23") Sinopsis: Otra forma equivalente de enunciar el teorema de Tales utilizando la semejanza de triángulos: Dos triángulos encajados (en la posición de Tales) son semejantes y en consecuencia sus lados son proporcionales.  Ejemplo 1 (1´14") Sinopsis:Ejemplo de aplicación del teorema de Tales. Ejemplo 2 (3´30") Sinopsis:Ejemplo de aplicación del teorema de Tales. Ejemplo 3 (3´24") Sinopsis:Ejemplo de aplicación del teorema de Tales. Ejemplo 4 (3´22") Sinopsis:Ejemplo de aplicación del teorema de Tales. Ejemplo 5 (2´10") Sinopsis:Ejemplo de aplicación del teorema de Tales. Ejemplo 5 (3´07") Sinopsis:Ejemplo de aplicación del teorema de Tales. |  |
