Plantilla:Criterios de semejanza de triángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:28 21 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema | + | Los criterios de semejanza de triángulos simplifican el número de condiciones que deben comprobarse para que dos triángulos sean semejantes: |
| + | |||
| + | {{Teorema_sin_demo | ||
| |titulo=Criterios de semejanza de triángulos | |titulo=Criterios de semejanza de triángulos | ||
| |enunciado= | |enunciado= | ||
| Línea 5: | Línea 7: | ||
| #Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales: <math>\widehat{A}=\widehat{A}',\ \widehat{B}=\widehat{B}'</math> | #Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales: <math>\widehat{A}=\widehat{A}',\ \widehat{B}=\widehat{B}'</math> | ||
| #Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido: <math>\frac {a}{a'} = \frac {b}{b'} \ , \ \widehat{C}=\widehat{C}'</math> | #Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido: <math>\frac {a}{a'} = \frac {b}{b'} \ , \ \widehat{C}=\widehat{C}'</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Criterios de semejanza de triángulos | ||
| + | |descripcion=Actividades para aprender y practicar los criterios de semejanza de triángulos. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena7/2quincena7_contenidos_2b.htm | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Criterios de semejanza de triángulos|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=32´54" | ||
| + | |url1=https://www.youtube.com/watch?v=D0kqQauTyPA&list=PLZNmE9BEzVIlfkGkycBHck7ZFTYKuEtnw&index=2 | ||
| + | |sinopsis=Tutorial en el que se explica y trabaja los criterios de semejanza de triángulos y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades. | ||
| - | |demo= | + | *00:00 a 06:08: Criterios de Igualdad (Congruencia) de Triángulos. |
| - | # | + | *06:08 a 08:30: Definición de Triángulos Semejantes. |
| - | #En efecto, si tienen dos ángulos respectivamente iguales, el tercero también lo tienen igual. Entonces, esos dos triángulos se pueden poner en la posición de Tales y, en consecuencia, son semejantes. | + | *08:30 a 15:30: 1er criterio de semejanza, lados proporcionales. |
| - | # | + | **11:00 - Ejemplo del 1er criterio de semejanza. |
| + | *15:30 a 21:30: 2º criterio de semejanza, ángulos iguales. | ||
| + | **17:00 - Ejemplo del 2º criterio de semejanza. | ||
| + | *21:30 a 26:30: 3er criterio de semejanza, ángulo igual y sus lados proporcionales. | ||
| + | **23:05 - Ejemplo del 3er criterio de semejanza. | ||
| + | *26:30 a 32:54 : Ejercicio donde se aplica la semejaza de triángulos. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=6'17" | ||
| + | |url1=https://www.youtube.com/watch?v=1QaGNAlZZJs&index=7&list=PLLfTN7MHLxCokf6CRoyuwfardoGhRZgLl | ||
| + | |sinopsis=Ejemplos de aplicación de los criterios de semejanza. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=2'16" | ||
| + | |url1=https://www.youtube.com/watch?v=wrlrwH4YE3I | ||
| + | |sinopsis=Los lados de un triángulo miden 3, 4 y 6 cm, y los lados de otro triángulo miden 9,12 y 18 cm. Comprueba si son semejantes. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=3'47" | ||
| + | |url1=https://www.youtube.com/watch?v=2qGrA0UO5iQ | ||
| + | |sinopsis=Dos ángulos de un triángulo miden 55º y 85º, y dos de los ángulos de otro triángulo miden 55º y 65º. ¿Son semejantes?. | ||
| + | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Problema 3 | ||
| + | |duracion=4'45" | ||
| + | |url1=https://www.youtube.com/watch?v=EifvQe3VR-o&index=8&list=PLLfTN7MHLxCokf6CRoyuwfardoGhRZgLl | ||
| + | |sinopsis=Cálculo altura inaccesible usando dos triángulos semejantes | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Los criterios de semejanza de triángulos simplifican el número de condiciones que deben comprobarse para que dos triángulos sean semejantes:
Criterios de semejanza de triángulos
- Dos triángulos son semejantes si tienen los lados proporcionales:
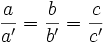
- Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
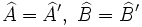
- Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
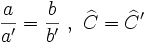
Criterios de semejanza de triángulos Descripción: Actividades para aprender y practicar los criterios de semejanza de triángulos.
Tutorial (32´54") Sinopsis:Tutorial en el que se explica y trabaja los criterios de semejanza de triángulos y se resuelven algunos ejercicios sencillos en los que se aplican dichas propiedades.
- 00:00 a 06:08: Criterios de Igualdad (Congruencia) de Triángulos.
- 06:08 a 08:30: Definición de Triángulos Semejantes.
- 08:30 a 15:30: 1er criterio de semejanza, lados proporcionales.
- 11:00 - Ejemplo del 1er criterio de semejanza.
- 15:30 a 21:30: 2º criterio de semejanza, ángulos iguales.
- 17:00 - Ejemplo del 2º criterio de semejanza.
- 21:30 a 26:30: 3er criterio de semejanza, ángulo igual y sus lados proporcionales.
- 23:05 - Ejemplo del 3er criterio de semejanza.
- 26:30 a 32:54 : Ejercicio donde se aplica la semejaza de triángulos.
Ejemplos (6'17") Sinopsis:Ejemplos de aplicación de los criterios de semejanza.
Problema 1 (2'16") Sinopsis:Los lados de un triángulo miden 3, 4 y 6 cm, y los lados de otro triángulo miden 9,12 y 18 cm. Comprueba si son semejantes.
Problema 2 (3'47") Sinopsis:Dos ángulos de un triángulo miden 55º y 85º, y dos de los ángulos de otro triángulo miden 55º y 65º. ¿Son semejantes?.
Problema 3 (4'45") Sinopsis:Cálculo altura inaccesible usando dos triángulos semejantes
Criterios de semejanza de triángulos Descripción: En esta escena podrás ver los tres criterios de semejanza de triángulos.
