Combinatoria
De Wikipedia
| Revisión de 09:25 24 sep 2017 Coordinador (Discusión | contribuciones) (→Combinaciones con repetición) ← Ir a diferencia anterior |
Revisión de 09:33 24 sep 2017 Coordinador (Discusión | contribuciones) (→Combinaciones con repetición) Ir a siguiente diferencia → |
||
| Línea 134: | Línea 134: | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado= | + | {{Teorema|titulo=Proposición|enunciado= |
| El número de combinaciones con repetición de n elementos tomados de k en k (n ≥ k) puede calcularse con la siguiente fórmula: | El número de combinaciones con repetición de n elementos tomados de k en k (n ≥ k) puede calcularse con la siguiente fórmula: | ||
| <center><math>CR^k_n = {n+k-1\choose k} = \frac{(n+k-1)!}{k! (n-1)!}</math></center> | <center><math>CR^k_n = {n+k-1\choose k} = \frac{(n+k-1)!}{k! (n-1)!}</math></center> | ||
| + | |demo=Ver una explicación de esta fórmula en: [https://es.wikipedia.org/wiki/Combinaciones_con_repetici%C3%B3n Combinaciones con repetición (Wikipedia)] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo|contenido=¿De cuántas maneras diferentes se pueden repartir 10 caramelos (indistinguibles) ente 4 niños? | ||
| + | |sol= | ||
| + | :<math>CR^10_4 = {4+10-1\choose 10} = {13\choose 10} = 286</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:33 24 sep 2017
Tabla de contenidos |
Permutaciones
Se llama permutaciones de n elementos, y se representa 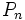 , a las distintas agrupaciones de n elementos ordenadas obtenidas a partir de esos n elementos.
, a las distintas agrupaciones de n elementos ordenadas obtenidas a partir de esos n elementos.
Proposición
El número de permutaciones de n elementos se pueden calcular con la siguiente fórmula:
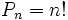
Demostración:
Si quiero formar ordenar n elementos, el primer elemento del grupo lo puedo escoger de n maneras distintas (puesto que dispongo de n elementos), el 2º de (n-1) maneras, el 3º de (n-2) maneras, ..., y el n-ésimo, de 1 sola manera. Multiplicando todas las posibilidades obtengo la fórmula.Calcula las permutaciones de 4 elementos sin repetición: 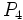
Calcula las permutaciones de 7 elementos sin repetición: 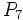
Calcula cuántos números de cuatro cifras diferentes (sin repetir la misma cifra) pueden formarse con los dígitos 3,5,7 y 9.
Di el número de posibles clasificaciones de los 9 nadadores que participan en una prueba de 100 m mariposa.
¿Cuántos números de 5 cifras se pueden formar con 5 dígitos distintos si no se pueden repetir las cifras? (Permutaciones sin repetición)
Permutaciones con repetición
Se llama permutaciones con repetición de n elementos, donde el primer elemento se repite "a" veces , el segundo "b" veces , el tercero "c" veces, ..., con n=a+b+c+..., y se representa 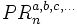 , a las distintas agrupaciones ordenadas de n elementos formadas con esos n elementos, teniendo en cuenta que los elementos repetidos son indistinguibles.
, a las distintas agrupaciones ordenadas de n elementos formadas con esos n elementos, teniendo en cuenta que los elementos repetidos son indistinguibles.
Proposición
El número de permutaciones con repetición de n elementos, donde el primer elemento se repite "a" veces , el segundo "b" veces , el tercero "c" veces, ..., con n=a+b+c+..., se pueden calcular con la siguiente fórmula:
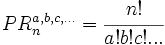
Demostración:
Las permutaciones ordinarias con n elementos son n!. Pero cada elemento repetido "a" veces se puede colocar de a! formas distintas, de manera que debo dividir n! por a! para quedarme solo con las formaciones no repetidas. Lo mismo se hace con los "b", "c", ... elementos repetidos, por lo que habrá que dividir también por b!, c!, ...Calcula las permutaciones de 12 elementos con repetición de 7,3 y 2: 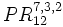
Calcula las permutaciones de 7 elementos con repetición de 3,2 y 2: 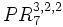
Una pareja ha tenido 3 niñas y 1 niño. ¿En cuántos órdenes diferentes los ha podido tener?
¿Cuántas palabras distintas, tengan o no sentido, podemos forma con las letras de la palabra ORDENADOR?
¿De cuántas maneras distintas podemos ordenar 3 bolas verdes, 2 rojas y 1 azul?
Combinaciones
Se llaman combinaciones de n elementos tomados de k en k (n ≥ k), y lo representaremos por 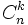 o
o 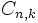 , a los distintos subconjuntos de k elementos que pueden formarse con los n elementos dados. Nótese que al tratarse de subconjuntos no importa el orden y no pueden repetirse los elementos.
, a los distintos subconjuntos de k elementos que pueden formarse con los n elementos dados. Nótese que al tratarse de subconjuntos no importa el orden y no pueden repetirse los elementos.
Proposición
El número de combinaciones de n elementos tomados de k en k (n ≥ k) puede calcularse con la siguiente fórmula:
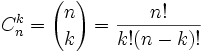
Demostración:
Si se tiene un conjunto con n elementos, de los cuales se van a escoger k de ellos, la selección (ordenada) puede hacerse de
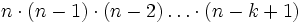
formas, ya que en el primer paso se tienen n opciones, en el segundo se tienen n-1, en el tercero n-2, y así sucesivamente, terminando en el paso k que tendrá n-k+1 opciones.
Ahora, para eleiminar los conjuntos repetidos, hay que dividir el producto anterior entre el número de selecciones "equivalentes" (conjuntos con los mismos elementos en distinto orden). Pero si se tiene k objetos, hay k! formas de permutarlos, es decir, k! formas de listarlos en distinto orden.
Concluimos que el número de subconjuntos con k elementos, escogidos de un conjunto con n elementos es
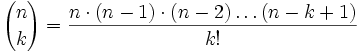
Multiplicando el numerador y el denominador por 
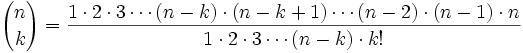
o lo que es lo mismo, expresado con factoriales:
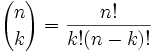
Combinaciones (sin repetición). Ejemplos.
Combinaciones (sin repetición). Ejemplos.
Combinaciones (sin repetición). Ejemplos.
Calcula 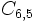
Calcula 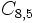
Calcula cuántos zumos de cuatro frutas distintos se pueden hacer con siete clases de fruta.
Vicente tiene 5 amigos y quiere salir cada sábado con 3 amigos diferentes. ¿Cuántos sábados podrá salir sin repetir?
Tenemos cuatro colores (verde, rojo, azul y amarillo). ¿Cuántas mezclas diferentes podemos hacer si los mezclamos dos a dos?
Tu profesora de Lengua Castellana te dice que, cuando acabes el curso, tienes que haber leído 3 libros de una lista de 5. ¿Cuántas posibles elecciones puedes hacer?
En un colegio una comisión consta de 2 profesores y 4 alumnos. ¿Cuántas comisiones distintas se pueden formar con 7 profesores y 10 alumnos?
Combinaciones con repetición
Se llaman combinaciones con repetición de n elementos tomados de k en k, y lo representaremos por 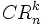 o
o 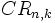 , a las distintas agrupaciones de k elementos que pueden formarse con los n elementos dados, de manera que pueden repetirse los elementos y no importa el orden de los mismos.
, a las distintas agrupaciones de k elementos que pueden formarse con los n elementos dados, de manera que pueden repetirse los elementos y no importa el orden de los mismos.
Nota: n no tiene por qué ser mayor o igual que k.
Proposición
El número de combinaciones con repetición de n elementos tomados de k en k (n ≥ k) puede calcularse con la siguiente fórmula:
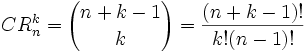
Ver una explicación de esta fórmula en: Combinaciones con repetición (Wikipedia)
¿De cuántas maneras diferentes se pueden repartir 10 caramelos (indistinguibles) ente 4 niños?
Variaciones con repetición
Se llama variaciones con repetición de n elementos tomados de k en k (n ≥ k), y se representa 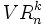 , o bien
, o bien 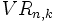 , a las distintas agrupaciones ordenadas de n elementos que se pueden formar a partir de m elementos dados en las que se pueden repetir los elementos.
, a las distintas agrupaciones ordenadas de n elementos que se pueden formar a partir de m elementos dados en las que se pueden repetir los elementos.
Proposición
El número de variaciones con repetición de n elementos tomados de k en k (n ≥ k) se pueden calcular con la siguiente fórmula:
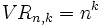
Demostración:
Si quiero formar grupos de n elementos en los que importa el orden, el primer elemento del grupo lo puedo escoger de n maneras distintas (puesto que dispongo de n elementos), el 2º también de n maneras (pues puedo repetirlo), el 3º también de n maneras, ..., y el k-ésimo, de n maneras distintas. Multiplicando todas las posibilidades obtengo la fórmula.Calcula 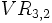
Calcula 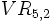
¿Cuántos números de dos cifras pueden formarse con los dígitos 1, 2 y 3, si se pueden repetir las cifras
Con las cifras 0, 1, 3, 5 y 7, ¿cuántos números de 4 cifras podemos escribir?
Variaciones ordinarias
Se llama variaciones ordinarias (o sin repetición) de n elementos tomados de k en k (n ≥ k), y se representa 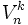 , o bien
, o bien 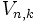 , a las distintas agrupaciones ordenadas de n elementos que se pueden formar a partir de m elementos dados en las que no se pueden repetir los elementos.
, a las distintas agrupaciones ordenadas de n elementos que se pueden formar a partir de m elementos dados en las que no se pueden repetir los elementos.
Proposición
El número de variaciones ordinarias de n elementos tomados de k en k (n ≥ k) se pueden calcular con la siguiente fórmula:
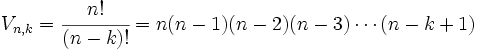
Demostración:
Si quiero formar grupos de n elementos en los que importa el orden, el primer elemento del grupo lo puedo escoger de n maneras distintas (puesto que dispongo de n elementos), el 2º de (n-1) maneras distintas (pues no puedo repetir el anterior), el 3º de (n-2), ..., y el k-ésimo, de (n-k+1) maneras distintas. Multiplicando todas las posibilidades obtengo la fórmula.Calcula 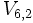
Calcula 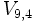
¿Cuántos números de dos cifras pueden formarse con los dígitos 1, 2 y 3, si no se pueden repetir las cifras.
Cuántos números de tres cifras no repetidas se pueden formar con los dígitos 2, 3, 4, 5 y 6? ¿Cuántos son pares?¿Cuántos terminan en 45?
En una competición participan 6 corredores pero sólo hay 3 premios distintos (1º, 2º y 3º). ¿De cuántas formas distintas pueden asignarse 3 los premios entre los 6 atletas?
Ejercicios y Problemas
Ejercicios y problemas resueltos sobre permutaciones.
Ejercicios y problemas resueltos sobre combinaciones.
Ejercicios y problemas resueltos sobre variaciones.
Problemas resueltos sobre combinatoria.
Problemas resueltos sobre combinatoria.
Ejercicios resueltos sobre ecuaciones con expresiones combinatorias.
Ejercicios de autoevaluación sobre combinatoria.
Autoevaluación sobre problemas de combinatoria.
Autoevaluación sobre problemas de combinatoria.

