Coordenadas geográficas (3ºESO Académicas)
De Wikipedia
| Revisión de 11:50 3 dic 2016 Coordinador (Discusión | contribuciones) (→Distancias en la esfera terrestre) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Apéndice) |
||
| Línea 22: | Línea 22: | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_estudiia | ||
| + | |titulo1=Esfera terrestre: elementos | ||
| + | |duracion=1'49" | ||
| + | |sinopsis=Videotutorial. | ||
| + | |url1=https://www.youtube.com/watch?v=3M-oqPa7fq8&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm&index=30 | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Coordenadas geográficas== | ==Coordenadas geográficas== | ||
| {{Tabla50|celda2=[[Imagen:coorde_geo.jpg|center]] | {{Tabla50|celda2=[[Imagen:coorde_geo.jpg|center]] | ||
| |celda1= | |celda1= | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Por cada punto de la superficie terrestre pasa un meridiano y un paralelo. Para referirnos a ellos tomaremos como referencia al ecuador y al meridiano de Greenwich. De esta manera, cada punto de la superficie terrestre queda determinado por unas '''coordenadas geográficas''' que son su latitud y su longitud, y que pasamos a definir: | + | Por cada punto de la superficie terrestre pasa un meridiano y un paralelo. Para referirnos a ellos tomaremos como referencia al ecuador y al meridiano de Greenwich. Definimos: |
| {{p}} | {{p}} | ||
| * La '''latitud''' de un punto de la superficie terrestre es la medida del ángulo del arco de meridiano que va desde dicho punto al ecuador. Al valor del ángulo se le añade la sigla N (norte) o S (sur), dependiendo del hemisferio al que pertenezca. Todos los puntos de un paralelo tienen la misma latitud. | * La '''latitud''' de un punto de la superficie terrestre es la medida del ángulo del arco de meridiano que va desde dicho punto al ecuador. Al valor del ángulo se le añade la sigla N (norte) o S (sur), dependiendo del hemisferio al que pertenezca. Todos los puntos de un paralelo tienen la misma latitud. | ||
| * La '''longitud''' de un punto de la superficie terrestre es la medida del ángulo que forma el plano que determina el meridiano en el que está el punto con el plano que determina el meridiano de Greenwich. También añadiremos la sigla E (este) u O (oeste), dependiendo de si el ángulo es en un sentido o en otro. | * La '''longitud''' de un punto de la superficie terrestre es la medida del ángulo que forma el plano que determina el meridiano en el que está el punto con el plano que determina el meridiano de Greenwich. También añadiremos la sigla E (este) u O (oeste), dependiendo de si el ángulo es en un sentido o en otro. | ||
| + | {{p}} | ||
| + | De esta manera, cada punto de la superficie terrestre queda determinado por unas '''coordenadas geográficas''': su latitud y su longitud. | ||
| }} | }} | ||
| Aclaremos esto un poco. El ecuador es el paralelo 0° y divide el globo en norte y sur; así el polo norte es 90°N y el polo sur es 90°S. | Aclaremos esto un poco. El ecuador es el paralelo 0° y divide el globo en norte y sur; así el polo norte es 90°N y el polo sur es 90°S. | ||
| Línea 37: | Línea 48: | ||
| El '''meridiano 180º''' o '''antimeridiano''' es el meridiano que forma un ángulo de 180° con respecto al meridiano de Greenwich. Es común para la longitud este u oeste. Se usa como base para la '''línea internacional de cambio de fecha''' porque en su mayoría atraviesa aguas abiertas del Océano Pacífico. De todos modos, el meridiano atraviesa algunos países, además de la Antártida. | El '''meridiano 180º''' o '''antimeridiano''' es el meridiano que forma un ángulo de 180° con respecto al meridiano de Greenwich. Es común para la longitud este u oeste. Se usa como base para la '''línea internacional de cambio de fecha''' porque en su mayoría atraviesa aguas abiertas del Océano Pacífico. De todos modos, el meridiano atraviesa algunos países, además de la Antártida. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_estudiia | ||
| + | |titulo1=Coordenadas geográficas | ||
| + | |duracion=3'00" | ||
| + | |sinopsis=Videotutorial. | ||
| + | |url1=https://www.youtube.com/watch?v=4-S_M19sCC0&index=31&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 50: | Línea 68: | ||
| ==Distancias en la esfera terrestre== | ==Distancias en la esfera terrestre== | ||
| - | {{Tabla75|celda2=[[Imagen=Ortodroma.png|thumb|Distancia ortodrómica entre dos puntos a lo largo de un círculo máximo sobre la superficie de una esfera.]] | + | {{Tabla75|celda2=[[Imagen:Ortodroma.png|thumb|Distancia ortodrómica entre dos puntos a lo largo de un círculo máximo sobre la superficie de una esfera.]] |
| |celda1= | |celda1= | ||
| Para puntos muy cercanos, la distancia entre dos puntos la solemos aproximar mediante medidas que se hacen siguiendo una línea recta, pero si los puntos están a muchos kilómetros de distancia, la linea recta ya no nos vale, hay que medir una línea curva. Pero entre dos puntos de la esfera hay muchas líneas curvas que los unen, ¿cuál tomamos?. Habrá que tomar la que mida menos de todas. Se puede comprobar que dicha curva es el arco de circunferencia máxima que pasa por los dos puntos y, en consecunecia, podemos dar la siguiente definición: | Para puntos muy cercanos, la distancia entre dos puntos la solemos aproximar mediante medidas que se hacen siguiendo una línea recta, pero si los puntos están a muchos kilómetros de distancia, la linea recta ya no nos vale, hay que medir una línea curva. Pero entre dos puntos de la esfera hay muchas líneas curvas que los unen, ¿cuál tomamos?. Habrá que tomar la que mida menos de todas. Se puede comprobar que dicha curva es el arco de circunferencia máxima que pasa por los dos puntos y, en consecunecia, podemos dar la siguiente definición: | ||
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | La '''distancia''' entre dos puntos de la esfera terrestre es la longitud del arco de circunferencia máxima que los une.}} | + | La '''distancia (ortodrómica)''' entre dos puntos de la esfera terrestre es la longitud del arco de circunferencia máxima que los une.}} |
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| Línea 70: | Línea 88: | ||
| |descripcion=Calcula la distancia entre dos ciudades de Costa Rica de las que puedes averiguar sus coordenadas geográficas haciendo uso de la escena interactiva. | |descripcion=Calcula la distancia entre dos ciudades de Costa Rica de las que puedes averiguar sus coordenadas geográficas haciendo uso de la escena interactiva. | ||
| |enlace=[https://ggbm.at/jF8d26ra Distancia entre dos ciudades conocidas sus coordenadas geográficas] | |enlace=[https://ggbm.at/jF8d26ra Distancia entre dos ciudades conocidas sus coordenadas geográficas] | ||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Escena para calcular la velocidad lineal a la que nos movemos debido a la rotación de la Tierra, según la latitud en que estemos situados. | ||
| + | |enlace=[https://ggbm.at/grTtgqPa How fast are you spinning?] | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejercicio resuelto: ''Coordenadas geográficas''|enunciado=Calcula cuántos miden los paralelos correspondientes a las latitudes 30º y 60º. (Dato: Radio terrestre aprox. 6371 km)|sol= | + | {{Ejemplo|titulo=Ejercicio resuelto: ''Coordenadas geográficas''|enunciado=Calcula cuánto miden los paralelos correspondientes a las latitudes 30º y 60º. (Dato: Radio terrestre aprox. 6371 km)|sol= |
| *El paralelo 60º mide 20015 km. | *El paralelo 60º mide 20015 km. | ||
| *El paralelo 30º mide 34646 km. | *El paralelo 30º mide 34646 km. | ||
| Línea 97: | Línea 121: | ||
| </center> | </center> | ||
| }} | }} | ||
| + | {{p}} | ||
| + | Muchos paises se han adaptado a horarios de otras naciones por conveniencia de luz, política, comercio, etc. | ||
| + | |||
| + | '''¿Por qué España peninsular tiene una hora más que Inglaterra y que Portugal estando los tes paises en el huso cero?.''' | ||
| + | |||
| + | Esto se debe a que durante la Segunda Guerra Mundial tuvo que adaptar su horario para compaginarse con Alemania que se halla en el Huso Uno Este. También Portugal para no estar muy lejos en relación con el horario de Inglaterra se adaptó al horario del Huso Cero, aun sabiendo que le correspondía el del Huso Uno Oeste. | ||
| + | |||
| + | |||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Huso horario''|enunciado=Si en Bilbao (longitud 3ºO) son las 12 h, ¿qué hora será en Estambul (longitud 29ºE)?|sol= | {{Ejemplo|titulo=Ejemplo: ''Huso horario''|enunciado=Si en Bilbao (longitud 3ºO) son las 12 h, ¿qué hora será en Estambul (longitud 29ºE)?|sol= | ||
| Línea 122: | Línea 154: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | + | ==Apéndice== | |
| + | {{AI_cidead | ||
| + | |titulo1=Esfera | ||
| + | |descripcion=Actividades en la que podrás ver cómo se genera una esfera y estudiar sus elementos. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena8/2quincena8_contenidos_3e.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejecicios de autoevaluación sobre la esfera. | ||
| + | |url1=https://www.vitutor.com/geo/esp/f_8e.html | ||
| + | |titulo1=Autoevaluación: ''Esferas'' | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 220)
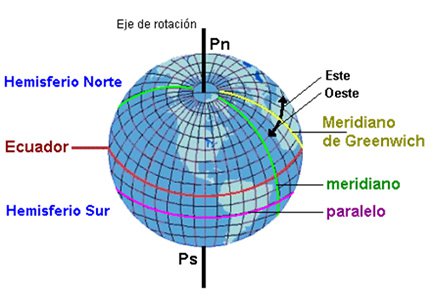
La esfera terrestre
La Tierra, al igual que otros astros, no es una esfera sino que, por efectos de la gravitación y de la fuerza centrífuga producida por su movimiento de rotación, está ligeramente achatada. Sin embargo, a efectos prácticos, la consideraremos una esfera.
|
Videotutorial.
Coordenadas geográficas
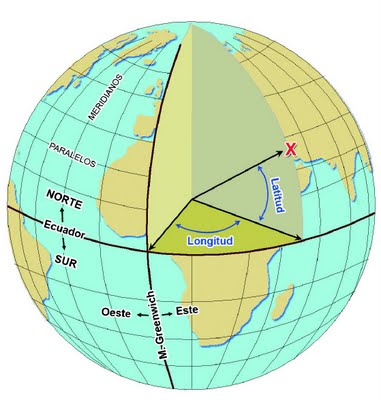
Por cada punto de la superficie terrestre pasa un meridiano y un paralelo. Para referirnos a ellos tomaremos como referencia al ecuador y al meridiano de Greenwich. Definimos:
De esta manera, cada punto de la superficie terrestre queda determinado por unas coordenadas geográficas: su latitud y su longitud. Aclaremos esto un poco. El ecuador es el paralelo 0° y divide el globo en norte y sur; así el polo norte es 90°N y el polo sur es 90°S. El meridiano de Greenwich es el meridiano 0º. En dirección este la longitud aumenta hasta llegar a 180º E y en dirección oeste hasta 180º O. El meridiano 180º o antimeridiano es el meridiano que forma un ángulo de 180° con respecto al meridiano de Greenwich. Es común para la longitud este u oeste. Se usa como base para la línea internacional de cambio de fecha porque en su mayoría atraviesa aguas abiertas del Océano Pacífico. De todos modos, el meridiano atraviesa algunos países, además de la Antártida. |
Videotutorial.
En esta escena podrás ver como se establecen las coordenadas geográficas de un punto de la supeficie terrestre.
En esta escena podrás localizar ciudades en el globo terrestre a partir de sus coordenadas geográficas.
Distancias en la esfera terrestre
| Para puntos muy cercanos, la distancia entre dos puntos la solemos aproximar mediante medidas que se hacen siguiendo una línea recta, pero si los puntos están a muchos kilómetros de distancia, la linea recta ya no nos vale, hay que medir una línea curva. Pero entre dos puntos de la esfera hay muchas líneas curvas que los unen, ¿cuál tomamos?. Habrá que tomar la que mida menos de todas. Se puede comprobar que dicha curva es el arco de circunferencia máxima que pasa por los dos puntos y, en consecunecia, podemos dar la siguiente definición:
La distancia (ortodrómica) entre dos puntos de la esfera terrestre es la longitud del arco de circunferencia máxima que los une. En esta escena podrás compara la distancia entre dos puntos de la Tierra con la misma latitud siguiendo el paralelo o el meridiano. Cálculo de la distancia entre dos ciudades cuyas coordenadas geográficas tienen la misma longitud. Calcula la distancia entre dos ciudades de Costa Rica de las que puedes averiguar sus coordenadas geográficas haciendo uso de la escena interactiva. Escena para calcular la velocidad lineal a la que nos movemos debido a la rotación de la Tierra, según la latitud en que estemos situados. |
Ejercicio resuelto: Coordenadas geográficas
Calcula cuánto miden los paralelos correspondientes a las latitudes 30º y 60º. (Dato: Radio terrestre aprox. 6371 km)
- El paralelo 60º mide 20015 km.
- El paralelo 30º mide 34646 km.
Husos horarios
| Un día es el tiempo que emplea la Tierra en dar una vuelta sobre sí misma y es equivalente a 24 horas. Si nos situamos en un meridiano concreto, cuando en él es mediodía, en su antimeridiano es medianoche. En cada meridiano, según su longitud , el mediodía se alcanza en un momento distinto. Si ajustásemos los relojes según ésto, en dos sitios próximos tendrían horas parecidas pero no iguales, lo cual resultaría caótico.
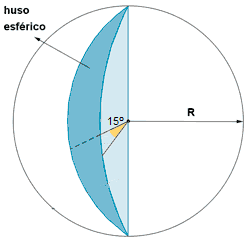
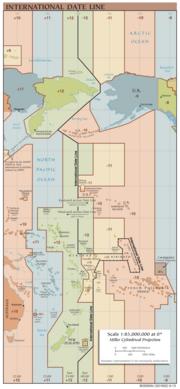
Por eso los cambios horarios se establecen por saltos que van de hora en hora, de la siguiente manera: Si dividimos 360º entre 24 h, obtendremos 24 husos esféricos de 15º. Son los llamados husos horarios. Dentro de la superficie se cada huso la hora es la misma. El huso horario correspondiente a España (salvo las Islas Canarias) se halla centrado en el meridiano de Greenwich y abarca desde la longitud 7º30'O hasta la longitud 7º30'E. Es el llamado huso horario cero. Cada meridiano múltiplo de 15° es el centro de un huso horario que abarca 7° y medio a cada lado. Los husos horarios se numeran, a partir del huso cero, como +1, +2, hasta +12 hacia el este, y -1, -2, hasta -12 hacia el oeste. No obstante, por razones prácticas, los paises que pisan dos husos distintos a veces mantienen la misma hora en ambas zonas, salvo que se trate de extensiones muy grandes, en cuyo caso dentro de un mismo pais puede manejarse varios horarios diferentes. España, por ejemplo, mantiene dos horas distintas: península e islas Canarias. Sin embargo, La Coruña (43°22′N 8°23′O), que pertenece al huso -1, tiene la misma hora que hay en toda la España peninsular, la mayor parte de la cual está dentro del huso cero. El huso +12 y el -12 serían el mismo y es dividido longitudinalmente por la mitad por la línea internacional del cambio de fecha o "International Date Line" (IDL). A ambos lados de la IDL es un día distinto. La línea internacional de cambio de fecha es una línea imaginaria superficial terrestre trazada sobre el océano Pacífico y "coincidente" con el meridiano 180º. La elección del meridiano 180° como la línea internacional de cambio de fecha se basa en la característica conveniente de que atraviesa zonas oceánicas prácticamente despobladas. Esta línea cruza el estrecho de Bering entre los territorios de Alaska y Siberia, aunque el meridiano 180º trascurre al este del paso, por lo cual las áreas a ambos lados tienen diferentes fechas, aunque la mayoría del recorrido se realiza por el océano Pacífico y no dificulta el mantenimiento de ninguna hora local. La solución de algunos países isleños, como Kiribati, es adaptar la hora legal o civil a la opción más conveniente. |
Cuando en el huso 0 es mediodía del lunes , en el huso -12 es medianoche y acaba de empezar el martes. |
Muchos paises se han adaptado a horarios de otras naciones por conveniencia de luz, política, comercio, etc.
¿Por qué España peninsular tiene una hora más que Inglaterra y que Portugal estando los tes paises en el huso cero?.
Esto se debe a que durante la Segunda Guerra Mundial tuvo que adaptar su horario para compaginarse con Alemania que se halla en el Huso Uno Este. También Portugal para no estar muy lejos en relación con el horario de Inglaterra se adaptó al horario del Huso Cero, aun sabiendo que le correspondía el del Huso Uno Oeste.
Ejemplo: Huso horario
Si en Bilbao (longitud 3ºO) son las 12 h, ¿qué hora será en Estambul (longitud 29ºE)?
Bilbao está en el huso horario cero porque 3º O está comprendido entre 7º30'O y 7º30'E.
Estambul está en el huso +2 porque 29ºE está en el huso centrado en el meridiano de longitud 30º.
Por tanto, si en Bilbao son las 12 h, en Estambul son las 14 h.Número de horas de sol en función del día del año, dependiendo de la localización geográfica.
Ejercicios propuestos
|
Ejercicios propuestos: Coordenadas geográficas |
Apéndice
Actividades en la que podrás ver cómo se genera una esfera y estudiar sus elementos.
Ejecicios de autoevaluación sobre la esfera.