Plantilla:Ángulos en un polígono de n lados
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:02 20 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema|titulo=Propiedad|enunciado= | + | {{Teorema|titulo=Propiedades|enunciado= |
| *La suma de los ángulos interiores de un polígono de <math>n\,</math> lados es igual a <math>(n-2) \cdot 180^\circ</math>. | *La suma de los ángulos interiores de un polígono de <math>n\,</math> lados es igual a <math>(n-2) \cdot 180^\circ</math>. | ||
| - | *Si el polígono de <math>n\,</math> lados es regular, cada ángulo interior mide <math>\cfrac{(n-2) \cdot 180^\circ}{n}</math> | + | *Si el polígono de <math>n\,</math> lados es regular: |
| + | **Cada ángulo interior mide <math>\cfrac{(n-2) \cdot 180^\circ}{n}</math>. | ||
| + | **Cada ángulo exterior mide <math>\cfrac{360^\circ}{n}</math>. | ||
| |demo= | |demo= | ||
| *Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º. | *Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º. | ||
| - | *Si además el polígono es regular, al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n. | + | *Si además el polígono es regular: |
| + | **Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n. | ||
| + | **Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior: | ||
| + | |||
| + | <center><math>180^\circ - \cfrac{(n-2) \cdot 180^\circ}{n}=\cfrac{n \cdot 180^\circ - (n-2) \cdot 180^\circ}{n}=\cfrac{360^\circ}{n}</math></center> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ángulos interiores de un polígono regular|enunciado= | + | |
| - | {{Video_enlace_carreon | + | {{Videotutoriales|titulo=Ángulos interiores de un polígono|enunciado= |
| + | {{Video_enlace | ||
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| + | |duracion=7´16" | ||
| + | |url1=https://www.youtube.com/watch?v=MbjzUC5p6lw | ||
| + | |sinopsis=*Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera. | ||
| + | *Ejemplos de aplicación. | ||
| + | *Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular. | ||
| + | }} | ||
| + | {{Video_enlace_yoestudio | ||
| + | |titulo1= Tutorial 2 | ||
| + | |duracion=3´24" | ||
| + | |url1=https://www.youtube.com/watch?v=2B5CzMnGjzg&index=13&list=PLkGU8edrdzbanv7OGbrAqJ0tLVNPTUiz_ | ||
| + | |sinopsis=Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados. | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1= Tutorial 3 | ||
| + | |duracion=6´13" | ||
| + | |url1=https://www.youtube.com/watch?v=kDIKukoGSGs&index=7&list=PLeySRPnY35dEHRD4tjlY_GULJ-MU-8tIx | ||
| + | |sinopsis=Suma de los ángulos interiores de un polígono. | ||
| + | }} | ||
| + | {{Video_enlace_carreon | ||
| + | |titulo1=Tutorial 4 | ||
| |duracion=9´02" | |duracion=9´02" | ||
| |url1=https://www.youtube.com/watch?v=ku_GwiCfIpk | |url1=https://www.youtube.com/watch?v=ku_GwiCfIpk | ||
| |sinopsis= | |sinopsis= | ||
| *Suma de los ángulos interiores de un triángulo. | *Suma de los ángulos interiores de un triángulo. | ||
| - | *Cálculo de los ángulos interiores de un polígono regular y de sus suma. | + | *Cálculo de los ángulos interiores de un polígono regular y de su suma. |
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1= Tutorial 2 | + | |titulo1= Tutorial 5 |
| |duracion=5´38" | |duracion=5´38" | ||
| |url1=https://www.youtube.com/watch?v=hDTEx-Z1qtU | |url1=https://www.youtube.com/watch?v=hDTEx-Z1qtU | ||
| |sinopsis=Ángulos interiores de un cuadrado y de un hexágono regular. | |sinopsis=Ángulos interiores de un cuadrado y de un hexágono regular. | ||
| }} | }} | ||
| - | {{Video_enlace_profealex | + | ---- |
| - | |titulo1= Tutorial 3 | + | {{Video_enlace_childtopia |
| - | |duracion=6´13" | + | |titulo1= Ejercicio |
| - | |url1=https://www.youtube.com/watch?v=kDIKukoGSGs&index=7&list=PLeySRPnY35dEHRD4tjlY_GULJ-MU-8tIx | + | |duracion=2´20" |
| - | |sinopsis=Suma de los ángulos interiores de un polígono regular. | + | |url1=https://www.youtube.com/watch?v=6VxDo2YQOQ8 |
| + | |sinopsis=¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene. | ||
| }} | }} | ||
| - | {{Video_enlace_yoestudio | ||
| - | |titulo1= Tutorial 4 | ||
| - | |duracion=3´24" | ||
| - | |url1=https://www.youtube.com/watch?v=2B5CzMnGjzg&index=13&list=PLkGU8edrdzbanv7OGbrAqJ0tLVNPTUiz_ | ||
| - | |sinopsis=Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados. | ||
| }} | }} | ||
| - | }} | + | {{Video_enlace_velazco |
| - | {{p}} | + | |titulo1=Ángulos exteriores de un polígono regular |
| - | {{Geogebra_enlace | + | |duracion=1´28" |
| - | |descripcion=En esta escena podrás ver los ángulos central, interior y exterior de un polígono regular de hasta 20 lados. | + | |url1=https://www.youtube.com/watch?v=90LSMGNvI20 |
| - | |enlace=[https://ggbm.at/C8Ta8fcW Ángulos en los polígonos regulares] | + | |sinopsis=Ángulo exterior de un polígono regular |
| }} | }} | ||
Revisión actual
Propiedades
- La suma de los ángulos interiores de un polígono de
lados es igual a 
.
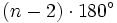- Si el polígono de lados es regular:
- Cada ángulo interior mide
.
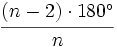- Cada ángulo exterior mide
.
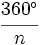- Cada ángulo interior mide
Demostración:
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
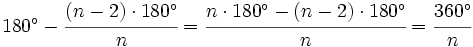
Tutorial 1 (7´16") Sinopsis:- Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular.
Tutorial 2 (3´24") Sinopsis: Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Tutorial 3 (6´13") Sinopsis: Suma de los ángulos interiores de un polígono.
Tutorial 4 (9´02") Sinopsis: - Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de su suma.
Tutorial 5 (5´38") Sinopsis: Ángulos interiores de un cuadrado y de un hexágono regular.
Ejercicio (2´20") Sinopsis:¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulos exteriores de un polígono regular (1´28") Sinopsis: Ángulo exterior de un polígono regular
