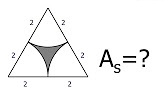Plantilla:Area sector circular
De Wikipedia
| Revisión de 18:09 17 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 4: | Línea 4: | ||
| [[Imagen:sector.png|160px]] | [[Imagen:sector.png|160px]] | ||
| |celda2={{p}} | |celda2={{p}} | ||
| + | * '''Longitud del arco:'''{{p}} | ||
| + | {{Caja|contenido=<math>l=\cfrac{2 \pi r \cdot \alpha}{360^o}=r \cdot \theta</math>}} | ||
| * '''Perímetro:'''{{p}} | * '''Perímetro:'''{{p}} | ||
| - | {{Caja|contenido=<math>l=\cfrac{2 \pi r \cdot \alpha}{360^o}; \ P = l+2 \cdot r</math>}} | + | {{Caja|contenido=<math>P = l+2 \cdot r</math>}} |
| * '''Área:'''{{p}} | * '''Área:'''{{p}} | ||
| - | {{Caja|contenido=<math>A=\cfrac{\pi r^2 \cdot \alpha}{360^o}=\cfrac{l \cdot r}{2}</math>}} | + | {{Caja|contenido=<math>A=\cfrac{\pi r^2 \cdot \alpha}{360^o}=\cfrac{l \cdot r}{2}=\cfrac{r^2 \cdot \theta}{2}</math>}} |
| |celda3={{p}} | |celda3={{p}} | ||
| * '''Elementos:''' | * '''Elementos:''' | ||
| Línea 13: | Línea 15: | ||
| :<math>l\;</math>: arco. | :<math>l\;</math>: arco. | ||
| :<math>\alpha\;\!</math>: ángulo (en grados sexagesimales). | :<math>\alpha\;\!</math>: ángulo (en grados sexagesimales). | ||
| + | :<math>\theta\;\!</math>: ángulo <math>\alpha\;</math> (en radianes). | ||
| * '''Nota:''' | * '''Nota:''' | ||
| :<math>\pi\;\!</math>: número Pi = 3,14159...{{p}} | :<math>\pi\;\!</math>: número Pi = 3,14159...{{p}} | ||
| :El perímetro es la longitud del arco más los dos radios. | :El perímetro es la longitud del arco más los dos radios. | ||
| }} | }} | ||
| - | }} {{p}} | ||
| {{Desplegable|titulo=Demostración:{{b}}|contenido= | {{Desplegable|titulo=Demostración:{{b}}|contenido= | ||
| La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres. | La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres. | ||
| Línea 30: | Línea 32: | ||
| de donde, sustituyendo el área del círculo por su valor, <math>\pi r^2\;\!</math>, se obtiene la fórmula. | de donde, sustituyendo el área del círculo por su valor, <math>\pi r^2\;\!</math>, se obtiene la fórmula. | ||
| - | + | ---- | |
| Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres. | Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres. | ||
| Línea 44: | Línea 46: | ||
| de donde, sustituyendo la longitud de la circunferencia por su valor, <math>2 \pi r\;\!</math>, se obtiene la fórmula. | de donde, sustituyendo la longitud de la circunferencia por su valor, <math>2 \pi r\;\!</math>, se obtiene la fórmula. | ||
| ---- | ---- | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Área del sector circular|enunciado= | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=4´37" | ||
| + | |url1=https://www.youtube.com/watch?v=Ro4NpV4VLTM | ||
| + | |sinopsis=Obtención del área de un sector circular. Ejemplo | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=11'37" | ||
| + | |sinopsis=Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 1) | ||
| + | |url1=https://www.youtube.com/watch?v=ZX7yP6lMWOQ&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=8 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 2 | ||
| + | |duracion=14'11" | ||
| + | |sinopsis=Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 2) | ||
| + | |url1=https://www.youtube.com/watch?v=lAq4wVrDxb4&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=9 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=11'39" | ||
| + | |sinopsis=Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 3) | ||
| + | |url1=https://www.youtube.com/watch?v=MUw3t6u_zXk&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=10 | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=7´49" | ||
| + | |url1=https://www.youtube.com/watch?v=vYSU_v0pTIk | ||
| + | |sinopsis=[[Imagen:areasombreada_1.jpg]]Halla el área sombreada de la figura. | ||
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Longitud del arco de circunferencia|enunciado= | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 1 | ||
| + | |duracion=16'15" | ||
| + | |sinopsis=Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 1) | ||
| + | |url1=https://www.youtube.com/watch?v=VJ2C0Zzw53o&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=5 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 2 | ||
| + | |duracion=20'42" | ||
| + | |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2) | ||
| + | |url1=https://www.youtube.com/watch?v=hCunrFdUM-g&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=6 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios 3 | ||
| + | |duracion=14'19" | ||
| + | |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3) | ||
| + | |url1=https://www.youtube.com/watch?v=Jic0vWAsr6U&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33&index=7 | ||
| + | }} | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Área del trapecio circular | ||
| + | |duracion=7'06" | ||
| + | |sinopsis=Deducción de la fórmula del área del trapecio circular. Ejemplo. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=vl2NF0wFINk | ||
| + | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente. | |descripcion=En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente. | ||
| - | |enlace=[https://ggbm.at/g94ejTfk Área del sector circular y longitud de su arco] | + | |enlace=[http://ggbm.at/g94ejTfk Área del sector circular y longitud de su arco] |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
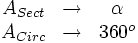
Despejando el área del sector:
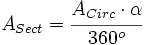
de donde, sustituyendo el área del círculo por su valor, 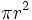 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
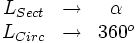
Despejando la longitud del sector:
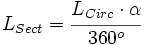
de donde, sustituyendo la longitud de la circunferencia por su valor, 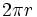 , se obtiene la fórmula.
, se obtiene la fórmula.
Obtención del área de un sector circular. Ejemplo
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 1)
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 2)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 3)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 1)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3)
Deducción de la fórmula del área del trapecio circular. Ejemplo.
En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente.
|
Actividad: El sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
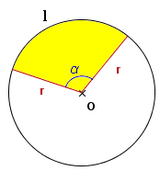
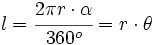
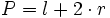
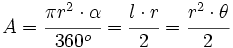
 : radio.
: radio.
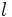 : arco.
: arco.
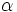 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).
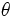 : ángulo
: ángulo  (en radianes).
(en radianes).
 : número Pi = 3,14159...
: número Pi = 3,14159...