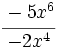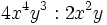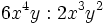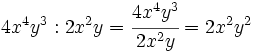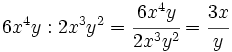Plantilla:Division de monomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:38 30 abr 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Entenderemos la división como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base. | + | Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base. |
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| Línea 15: | Línea 15: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Videotutoriales|titulo=División de monomios|enunciado= |
| - | |titulo1=Ejemplos: ''División de monomios'' | + | {{Video_enlace_paps |
| + | |titulo1=División de monomios | ||
| + | |duracion=6'54" | ||
| + | |sinopsis=Aprende a dividir monomios | ||
| + | |url1=https://www.youtube.com/watch?v=Jbq7lk69NTk | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1 | ||
| |duracion=9'07" | |duracion=9'07" | ||
| - | |sinopsis=Multiplica: | + | |sinopsis=Divide: |
| - | :a) <math>(8x^4y3z) : (-4x^2yz)\;</math> | + | :a) <math>(8x^4y^3z) : (-4x^2yz)\;</math> |
| :b) <math>(-15a^6b^3c^2) : (-3a^2b^3c)\;</math> | :b) <math>(-15a^6b^3c^2) : (-3a^2b^3c)\;</math> | ||
| - | :c) <math>(-\cfrac{2}{9}p^{10m}q^{6n}) : (-\cfrac{8}{3}p^{6m}q^{n})\;</math> | + | :c) <math>(-\cfrac{2}{9} \ p^{10m}q^{6n}) : (-\cfrac{8}{3} \ p^{6m}q^{n})\;</math> |
| - | |url1=https://www.youtube.com/watch?v=2PWac_RQ6lc}} | + | |url1=https://www.youtube.com/watch?v=2PWac_RQ6lc |
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=11'33" | ||
| + | |sinopsis=Divide los siguientes monomios: | ||
| + | |||
| + | :54) <math>\cfrac{50x^4}{25x^2}\;</math> ; {{b4}} 55) <math>\cfrac{25x^3}{5x}\;</math> ; {{b4}} 56) <math>\cfrac{-15x^3}{5x^2}\;</math> ; {{b4}} 57) <math>\cfrac{-45x^4}{9x}\;</math> | ||
| + | |||
| + | :58) <math>\cfrac{-18x^2}{-5x}\;</math> ; {{b4}} 59) <math>\cfrac{-7x^4}{-3x^3}\;</math> ; {{b4}} 60) <math>\cfrac{4x^3}{-2x^2}\;</math> ; {{b4}} 61) <math>\cfrac{-16x^2}{8x^2}\;</math> | ||
| + | |||
| + | :62) <math>\cfrac{-7x^3}{-3x^2}\;</math> ; {{b4}} 63) <math>\cfrac{10x^5}{5x^4}\;</math> ; {{b4}} 64) <math>\cfrac{20x^4}{-5x^4}\;</math> ; {{b4}} 65) <math>\cfrac{-5x^6}{-2x^4}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=oMIUcfhMTsA&index=12&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU | ||
| + | }} | ||
| + | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Aprende a dividir monomios
Divide:
- a)
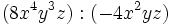
- b)
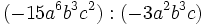
- c)
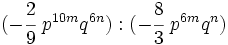
Divide los siguientes monomios:
- 54)
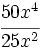 ; 55)
; 55) 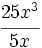 ; 56)
; 56) 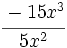 ; 57)
; 57) 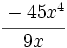
- 58)
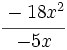 ; 59)
; 59) 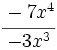 ; 60)
; 60) 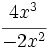 ; 61)
; 61) 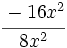
- 62)
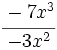 ; 63)
; 63) 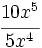 ; 64)
; 64) 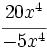 ; 65)
; 65)