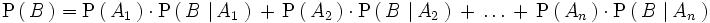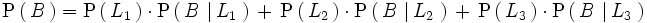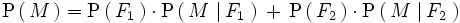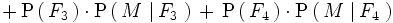Probabilidad. Combinatoria
De Wikipedia
| Revisión de 18:43 30 jun 2007 Juanmf (Discusión | contribuciones) (→Espacio muestral) ← Ir a diferencia anterior |
Revisión de 18:44 30 jun 2007 Juanmf (Discusión | contribuciones) (→Espacio muestral) Ir a siguiente diferencia → |
||
| Línea 17: | Línea 17: | ||
| . | . | ||
| }} | }} | ||
| + | <br> | ||
| {{Ejemplo|titulo=Ejemplo: ''Espacio muestral'' | {{Ejemplo|titulo=Ejemplo: ''Espacio muestral'' | ||
| Línea 34: | Línea 35: | ||
| |enunciado= '''1'''.Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: | |enunciado= '''1'''.Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: | ||
| - | a) Lanzar tres monedas. | + | a) Lanzar tres monedas. |
| - | b) Lanzar tres dados y anotar la suma de los puntos obtenidos. | + | |
| - | c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. | + | b) Lanzar tres dados y anotar la suma de los puntos obtenidos. |
| + | |||
| + | c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. | ||
| + | |||
| d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos. | d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos. | ||
| |sol= | |sol= | ||
| - | Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: | + | a) Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: |
| E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} | E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} | ||
| - | E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} | + | b) E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} |
| - | Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: | + | c) Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: |
| E={BB,BN,NN} | E={BB,BN,NN} | ||
| - | Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: | + | d) Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: |
| E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} | E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} | ||
Revisión de 18:44 30 jun 2007
Tabla de contenidos |
Experimentos aleatorios
Los fenómenos o experimentos aleatorios son los que pueden dar lugar a varios resultados, sin que pueda ser previsible enunciar con certeza cuál de estos va a ser observado en la realización del experimento.
Espacio muestral
Espacio muestral es el conjunto formado por todos los resultados de un experimento o fenómeno aleatorio. Lo denotamos con la letra E .
Ejemplo: Espacio muestral
El espacio muestral asociado al lanzamiento de dos dados y anotar la suma de los puntos
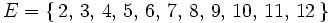
|
Ejercicios:Espacio muestral 1.Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: a) Lanzar tres monedas. b) Lanzar tres dados y anotar la suma de los puntos obtenidos. c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos.Solución: a) Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} b) E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} c) Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: E={BB,BN,NN} d) Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} |
Sucesos
Suceso de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral E . Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas.
Al conjunto de todos los sucesos que ocurren en un experimento aleatorio se le llama espacio de sucesos y se designa por S .
Ejemplo: Sucesos
En el ejemplo anterior, determina los sucesos de E:
a)Salir múltiplo de 5. b)Salir número primo. c)Salir mayor o igual que 10.
a)Salir múltiplo de 5:
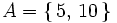
b)Salir número primo:
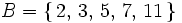
c)Salir mayor o igual que 10:
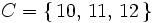
Analicemos los tipos mas frecuentes de sucesos.
Sucesos elementales son los que están formados por un solo resultado del
experimento.
Sucesos compuestos son los que estan formados por dos o más resultados del
experimento; es decir, por dos o más sucesos elementales.
Suceso seguro es el que se verifica al realizar el experimento aleatorio. Está
formado por todos los resultados posibles del experimento y, por tanto, coincide con el
espacio muestral.
Suceso imposible es el que nunca se verifica. Se representa por
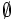 .
.
Operaciones con sucesos
Inclusión e igualdad de sucesos
Un suceso
A
esta incluido ( contenido ) en otro suceso
B
si todo suceso elemental de
A
pertenece también a
B
. Se representa por
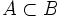 .
.
Dos suceso
A
y
B
son iguales si están formados por los mismos sucesos elementales. Se representa
por
A = B
.
Unión de sucesos
Si tenemos dos sucesos
A
y
B
de un mismo experimento aleatorio, llamamos suceso unión de
A
y
B
al suceso que se realiza cuando lo hacen
A
o
B
. Se representa por
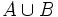 .
.
Intersección de sucesos
Si tenemos dos sucesos
A
y
B
de un mismo experimento aleatorio, llamamos suceso intersección de
A
y
B
al suceso que se realiza cuando lo hacen
A
y
B
. Se representa por
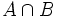 .
.
Cuando
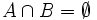 , decimos que los sucesos
A
y
B
son incompatibles. Cuando no sucede esto, decimos que
A
y
B
son compatibles.
, decimos que los sucesos
A
y
B
son incompatibles. Cuando no sucede esto, decimos que
A
y
B
son compatibles.
Sucesos contrarios
Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos conjuntos da el conjunto imposible, decimos que ambos sucesos son complementarios o contrarios.
Para un suceso cualquiera
A
de un experimento aleatorio, llamamos suceso contrario del suceso
A
al suceso que se verifica cuando no se verifica
A
, y reciprocamente. Se representa:
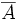 .
.
En cualquier experimento aleatorio, todo suceso que se considere tiene su contrario. Las
propiedades mas significativas de los sucesos contrarios son:
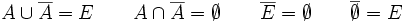
Algebra de Boole de sucesos
La union y la interseccion de sucesos verifican las propiedades conmutativa, asociativa,
idempotente, simplificación, distributiva, existencia de elemento neutro y absorción:
Definición de probabilidad. Propiedades.
Un experimento aleatorio se caracteriza porque repetido muchas veces y en idénticas condiciones el cociente entre el número de veces que aparece un resultado (suceso) y el número total de veces que se realiza el experimento tiende a un número fijo. Esta propiedad es conocida como ley de los grandes números, establecida por Jakob Bernouilli.
Probabilidad de un suceso es el número al que tiende la frecuencia relativa asociada al suceso a medida que el número de veces que se realiza el experimento crece.
Regla de Laplace
Definición de Laplace. En el caso de que todos los sucesos elementales del espacio muestral E sean equiprobables, Laplace define la probabilidad del suceso A como el cociente entre el número de resultados favorables a que ocurra el suceso A en el experimento y el número de resultados posibles del experimento.
|
|
Ejemplo: Regla de Laplace
En una baraja de 40 cartas, ¿cuál es la probabilidad de AS?, ¿Y de OROS
P(As)=número de ases/número total de cartas=4/40=0.1
P(OROS)=número de oros/número total de cartas=10/40=0.25Definición axiomática
La definición axiomática de probabilidad se debe a Kolmogorov, quien consideró la relación entre la frecuencia relativa de un suceso y su probabilidad cuando el número de veces que se realiza el experimento es muy grande.
Sea E el espacio muestral de cierto experimento aleatorio. La Probabilidad de cada suceso es un número que verifica:
- 1º. Cualquiera que sea el suceso A, P(A)
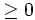 .
.
- 2º. Si dos sucesos son incompatibles, la probabilidad de su unión es igual a la suma de sus probabilidades.
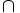 B =
B = 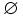
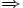 P(A
P(A 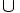 B) = P(A) + P(B).
B) = P(A) + P(B).
- 3º. La probabilidad total es 1. P(E) = 1.
Propiedades
- 1.
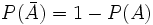
- 2.
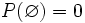
- 3. Si
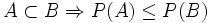
- 4. Si A1,A2,...,Ak son incompatibles dos a dos, entonces:
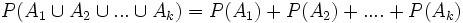
- 5.
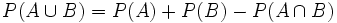
|
Ejercicios: Utilización de las propiedades 1. En una baraja hemos suprimido varia cartas. Entre las que quedan, se dan las siguientes probabilidades de ser extraídas: P(REY)=0.15, P(BASTOS)=0.3, P("carta que no sea REY ni BASTOS")=0.6. ¿Está entre ellas el REY de BASTOS? En caso afirmativo, da su probabilidad. ¿Cuántas cartas hay?Solución: a) 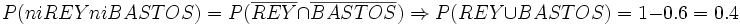
Sustituyendo:
2. En una caja tenemos 15 bolas blancas, 30 bolas negras y 45 bolas verdes. Si extraemos tres bolas simultáneamente, ¿cuál es la probabilidad de que salga una bola de cada color?
Solución: Calcularemos los casos posibles del experimento y los casos favorables al suceso del enunciado para aplicar la regla de Laplace. Los casos posibles son las distintas formas de extraer 3 bolas entre 90. Como el orden no debe tenerse en cuenta, estos casos son: 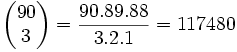
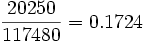 3. Si escogemos al azar dos números de teléfono y observamos la última cifra de cada uno, determina las probabilidades siguientes: a) Que las dos cifras sean iguales b) Que su suma sea 11 c) Que su suma sea mayor que 7 y menor que 13Solución: El espacio muestral de este experimento está formado por los cien sucesos elementales: 00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, ..., 98, 99. Para cada sucesos del enunciado calculamos sus casos favorables, aplicamos la regla de Laplace y obtenemos: Los casos favorables son: 00, 11, 22, ..., 99. La probabilidad de que las últimas cifras sean iguales es: P(últimas cifras iguales) = 10/100 = 1/10 = 0.1 Los casos favorables a que la suma de las últimas cifras sea 11 son: 29, 38, 47, 56, 65, 74, 83 y 92. Por tanto, P(últimas cifras suman once) = 8/100 = 0.08 Deben contarse los números de dos cifras cuya suma sea 8, 9, 10, 11 y 12. Haciendo un recuento ordenado, se obtienen 43 casos favorables. La probabilidad buscada es: P(últimas cifras suman un valor mayor que 7 y menor que 13) = 43/100 = 0.434. Se lanzan dos dados equilibrados con seis caras marcadas con los números del 1 al 6. Se pide: a) Halla la probabilidad de que la suma de los valores que aparecen en la cara superior sea múltiplo de tres. b) ¿Cuál es la probabilidad de que los valores obtenidos difieran en una cantidad mayor de dos?Solución: a) El espacio muestral del experimento es: E = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); ...; (6,6)} y está formado por 36 sucesos elementales equiprobables. Constituyen el número de casos posibles del experimento. Utilizando la regla de Laplace, calculamos las probabilidades de los sucesos que nos piden: Si llamamos A al suceso "obtener una suma múltiplo de 3", los casos favorables al suceso A son: A = {(1,2); (2,1); (1,5); (2,4); (3,3); (4,2); (5,1); (3,6); (4,5); (5,4); (6,3); (6,6)}. Por tanto, P( A ) = 12/36 = 1/3
B = {(1,4); (4,1); (1,5); (5,1); (1,6); (6,1); (2,5); (5,2); (2,6); (6,2); (3,6);(6,3)}.
5.Se tiran tres dados al mismo tiempo. Encuentra la probabilidad de que: a) La suma de los números aparecidos sea menor que 8. b) La suma de los números sea mayor que 4 y menor que 8.Solución: Los casos posibles de este experimento son las 216 ternas siguientes: 111, 112, 121, 211, ..., 665, 666. Realizando un recuento ordenado de los casos favorables a los sucesos del enunciado, obtenemos las siguientes probabilidades: a) P(suma de valores menor que 8)= 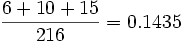 |
Probabilidad condicionada
Llamamos probabilidad condicionada del suceso
B
respecto del suceso
A
, y lo denotamos por
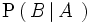 al cociente
al cociente
|
|
Ejemplo: Probabilidad condicionada
Se lanzan dos dados. Si la suma ha sido 7, ¿cuál es la probabilidad de que alguno de los dados haya salido un tres?
Sean los sucesos
A = "la suma de los puntos es siete" y
B = "en alguno de los dados ha salido un tres"
El suceso
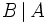 es salir en algún dado 3, si la suma ha sido 7. Observamos que esta situación
ocurre en las parejas
es salir en algún dado 3, si la suma ha sido 7. Observamos que esta situación
ocurre en las parejas
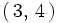 y
y
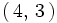 . Por tanto,
. Por tanto,
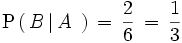
Ejercicios resueltos: Probabilidad condicionada
Independencia de sucesos
Decimos que dos sucesos
A
y
B
son independientes entre sí si la ocurrencia de uno de ellos no modifica
la probabilidad del otro, es decir, si:
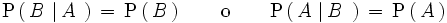
o lo que es lo mismo:
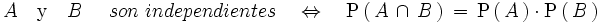
|
Ejercicios:Independencia de sucesos
1.. Calcula la probabilidad de que al extraer 3 cartas, con reemplazamiento, de una baraja española, sean todas copas.
Solución: Como la carta extraída se vuelve a introducir, los sucesos son independientes y la probabilidad buscada es:
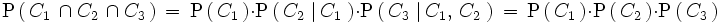
2.. Calcula la probabilidad de que al extraer 3 cartas, sucesivamente, de una baraja española, sean todas copas.
Solución: En este caso, los sucesos
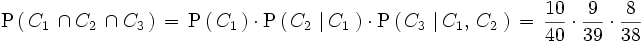
|
Probabilidad de aprobar cuando sólo se domina parte de la asignatura
Probabilidad de meter un gol en una tanda de penaltis
Probabilidad de obtener dos números pares lanzando dos dados
Probabilidad total
Llamamos sistema completo de sucesos a una familia de sucesos A1,A2,...,An que cumplen:
- 1. Son incompatibles dos a dos,
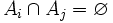
- 2. La unión de todos ellos es el suceso seguro,
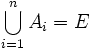
Teorema de la probabilidad total:
Sea A1,A2,...,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai), entonces:
|
|
|
Ejercicios:Probabilidad total
1.. Una compañía dedicada al transporte público explota tres líneas de una ciudad, de forma que el 60% de los autobuses cubre el servicio de la primero línea, el 30% cubre la segunda y el 10% cubre el servicio de la tercera línea. Se sabe que la probabilidad de que, diariamente, un autobús se averíe es del 2%, 4% y 1%, respectivamente, para cada línea. Determina la probabilidad de que, en un día, un autobús sufra una avería.
Solución: El suceso "sufrir una avería" (B) puede producirse en las tres líneas, (L1, L2, L3). Según el teorema de la probabilidad total, tenemos:
2..Una empresa del ramo de la alimentación elabora sus productos en cuatro factorías: F1, F2, F3 y F4. El porcentaje de producción total que se fabrica en cada factoría es del 40%, 30%, 20% y 10%, respectivamente, y además el porcentaje de envasado incorrecto en cada factoría es del 1%, 2%, 7% y 4%. Tomamos un producto de la empresa al azar. ¿Cuál es la probabilidad de que se encuentre defectuosamente envasado?
Solución: Llamando M = "el producto está defectuosamente envasado", se tiene que este producto puede proceder de cada una de las cuatro factorías y, por tanto, según el teorema de la probabilidad total tenemos:
3..Se lanzan dos monedas al aire. Si salen dos caras, se extrae una bola de una urna I, que contiene 2 bolas blancas y 3 negras. Si sale cara y cruz, se extrae una bola de una urna II, que contiene 4 bolas blancas y 1 negra. Si salen dos cruces, se extrae una bola de una urna III, que contiene 3 bolas blancas y 2 negras. ¿Cuál es la probabilidad de extraer bola blanca después de lanzar las monedas y sacar la bola?
Solución: 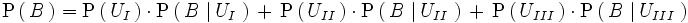
|
Teorema de Bayes
Sean
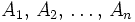 sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea
B
un suceso cualquiera del que se conocen las probabilidades condicionales
sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea
B
un suceso cualquiera del que se conocen las probabilidades condicionales
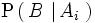 .
.
Entonces las probabilidades
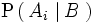 vienen dadas por la expresión:
vienen dadas por la expresión:
|
|
Demostración
Por definición de probabilidad condicionada
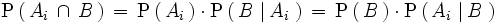
despejando
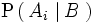 , se tiene:
, se tiene:
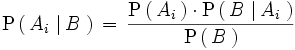
La probabilidad
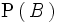 , por el teorema de la probabilidad total, es igual a
, por el teorema de la probabilidad total, es igual a
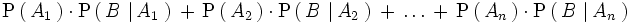
Sustituyendo en la ecuación anterior, obtenemos la fórmula de Bayes.
Ejemplo:Teorema de Bayes
Tenemos tres urnas: U1 con tres bolas rojas y cinco negras, U2 con dos bolas rojas y una negra y U3 con dos bolas rojas y tres negras. Escogemos una urna al azar y extraemos una bola. Si la bola ha sido roja, ¿cuál es la probabilidad de haber sido extraída de la urna U1 ?
Llamamos
R
al suceso sacar bola roja. La probabilidad pedida es
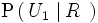 . Utilizando el teorema de Bayes, tenemos:
. Utilizando el teorema de Bayes, tenemos:
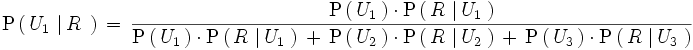
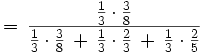

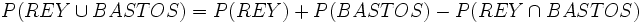
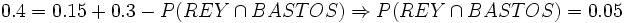
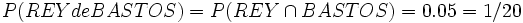
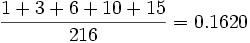
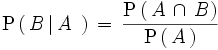
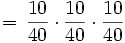
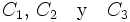 no son independientes.
no son independientes.