Plantilla:Potencias de números fraccionarios
De Wikipedia
| Revisión de 07:16 13 sep 2016 Coordinador (Discusión | contribuciones) (→Potencias de exponente negativo) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Potencias de números racionales) |
||
| Línea 1: | Línea 1: | ||
| - | ==Potencias de números fraccionarios== | + | ==Potencias de números racionales== |
| - | Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.{{p}} | + | Las potencias cuya base es un número racional se definen de la misma manera que las que tienen como base un número entero. |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido=Pulsa los botones para obtener ejemplos de cada tipo:{{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias2_1.html | + | |
| - | width=540 | + | |
| - | height=240 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias2_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| {{p}} | {{p}} | ||
| - | <center><iframe> | + | {{Videos: Potencia de un racional}} |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias2_2.html | + | |
| - | width=680 | + | |
| - | height=380 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias2_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | Tan sólo queda añadir el siguiente caso: | + | |
| ===Potencias de exponente negativo=== | ===Potencias de exponente negativo=== | ||
| {{Def potencia exponente entero}} | {{Def potencia exponente entero}} | ||
| - | + | {{p}} | |
| - | {{AI2|titulo=Actividad Interactiva: ''Potencias de exponente negativo''|cuerpo= | + | {{AI potencias exponente entero}} |
| - | {{ai_cuerpo | + | {{p}} |
| - | |enunciado='''Actividad 1.''' Potencias de exponente negativo. | + | ===Propiedades de las potencias de números racionales=== |
| - | |actividad= | + | Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.{{p}} |
| - | Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: | + | {{Ejemplos: propiedades potencias racionales}} |
| - | + | {{p}} | |
| - | a) <math>3^{-5}</math>{{b}}b) <math>5^{-3}</math>{{b}}c) <math>7^{-2}</math>{{b}}d) <math>2^{-7}</math> | + | {{Videos ejemplos propiedades potencias racionales}} |
| - | + | {{p}} | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias31_2.html | + | |
| - | width=450 | + | |
| - | height=250 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias31_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba. | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2.''' Autoevaluación. | + | |
| - | |actividad= | + | |
| - | Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias1_3.html | + | |
| - | width=630 | + | |
| - | height=260 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias1_3.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
Revisión actual
Potencias de números racionales
Las potencias cuya base es un número racional se definen de la misma manera que las que tienen como base un número entero.
- Breve repaso de las potencias de base entera y exponente natural.
- Potencias de base racional y exponente natural.
- Potencias de exponente 0 y 1.
Cómo se calcula la potencia de una fracción. Ejemplos.
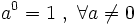 . Ejemplos.
. Ejemplos.
- Escribe en forma de potencia los siguientes productos:
- 1)
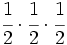
- 2)
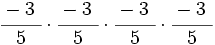
- 3)
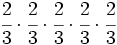
- Escribe en forma de una única potencia:
- 4)
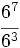 ; 5)
; 5) 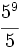 ; 6)
; 6) 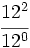
- 7)
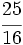 ; 8)
; 8) 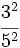 ; 9)
; 9) 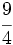 ; 10)
; 10) 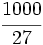
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
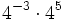
- b)
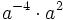
- c)
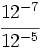
- d)
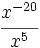
Simplifica:
- a)
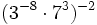
- b)
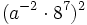
- c)
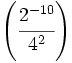
Halla el valor de:
11) 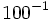 ; 12)
; 12) 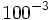 ; 13)
; 13) 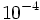 ; 14)
; 14) 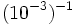
15) 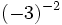 ; 16)
; 16) 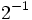 ; 17)
; 17) 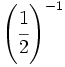 ; 18)
; 18) 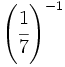 ; 19)
; 19) 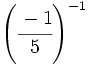
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 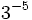 b)
b) 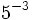 c)
c) 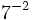 d)
d) 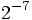
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.Tutorial muy completo que explica las propiedades básicas de las potencias con ejemplos resueltos sencillos y alguno más complejo.
- Potencias de exponente entero de números racionales.
- Propiedades.
- Ejemplos
Producto de potencias de fracciones con la misma base. Ejemplos.
Cociente de potencias de fracciones con la misma base. Ejemplos.
Potencia de otra potencia de una fracción. Ejemplos.
Potencia de un producto de fracciones. Ejemplos.
Producto de potencias de la misma base: 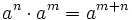 . Ejemplos.
. Ejemplos.
Cociente de potencias de la misma base: 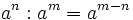 . Ejemplos.
. Ejemplos.
Potencia de otra potencia: 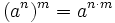 . Ejemplos.
. Ejemplos.
Potencia de un producto: 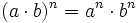 . Ejemplos.
. Ejemplos.
Potencia de un cociente: 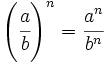 . Ejemplos.
. Ejemplos.
- Potencias de exponente 1 y 0.
- Producto y cociente de potencias de la misma base.
- Potencia de un producto y de un cociente.
- Potencia de otra potencia.
- Ejemplos.
- Potencias de base negativa.
- Potencias de exponente negativo.
- Ejemplos.
Cálculos con potencias de exponente positivo.
Cálculos con potencias de exponente negativo.
Simplificaciones de operaciones con potencias.
Cálculos con potencias de fracciones:
Calcula:
20) 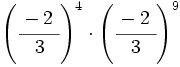 ; 21)
; 21) 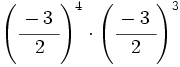 ; 22)
; 22) 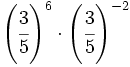
23) 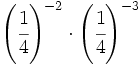 ; 24)
; 24) 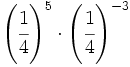 ; 25)
; 25) 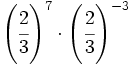
26)  ; 27)
; 27) 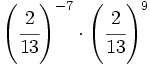 ; 28)
; 28) 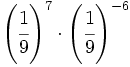
Calcula:
29) 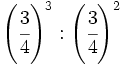 ; 30)
; 30)  ; 31)
; 31) 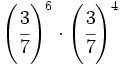
32) 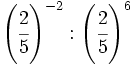 ; 33)
; 33) 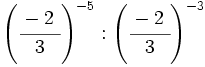 ; 34)
; 34) 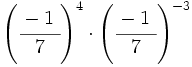
Calcula:
- 35)
![\left[ \left( \cfrac{-3~}{7} \right)^2 \right]^3](/wikipedia/images/math/0/d/5/0d5ecdfc87205ac8f368d6a70a5e1225.png) ; 36)
; 36) ![\left[ \left( \cfrac{2}{3} \right)^3 \right]^5](/wikipedia/images/math/2/9/c/29cf02b990eee91e9f5267cd7ae27ab8.png) ; 37)
; 37) ![\left[ \left( \cfrac{3}{4} \right)^2 \right]^4](/wikipedia/images/math/8/5/9/85905a10045ecdadf0d87cb496b46fd4.png)
- 38)
![\left[ \left( \cfrac{2}{5} \right)^3 \right]^2](/wikipedia/images/math/7/7/c/77ccd9469ab61459b42b5c42c31b6a03.png) ; 39)
; 39) ![\left[ \left( \cfrac{2}{3} \right)^{-2} \right]^{-3}](/wikipedia/images/math/7/1/7/717d66168670db7c17604eed1ecc5697.png) ; 40)
; 40) ![\left[ \left( \cfrac{3}{5} \right)^{-2} \right]^{-7}](/wikipedia/images/math/7/d/5/7d5523f771792c7a7444cc796d7a29e6.png)
- 41)
![\left[ \left( \cfrac{-3~}{4} \right)^{-2} \right]^{-5}](/wikipedia/images/math/d/e/2/de20c03afc7ad82625777cdcf282c409.png) ; 42)
; 42) ![\left[ \left( \cfrac{-2~}{7} \right)^3 \right]^{-2}](/wikipedia/images/math/d/8/f/d8f17a4b8bd520d1104f16e3bbe69742.png) ; 43)
; 43) ![\left[ \left( \cfrac{-2~}{7} \right)^{-1} \right]^3](/wikipedia/images/math/d/9/9/d996341203e6a65e266433c712564961.png)
- 44)
![\left[ \left( \cfrac{2}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/e/2/b/e2b4f1793a567fb108f0a0c11c815bcb.png) ; 45)
; 45) ![\left[ \left( \cfrac{-2~}{5} \right)^{-3} \right]^{-2}](/wikipedia/images/math/1/5/4/154452bc7b4e3830e7474ee197167695.png) ; 46)
; 46) ![\left[ \left( \cfrac{-1~}{8} \right)^{-2} \right]^{-3}](/wikipedia/images/math/d/f/7/df755b98eccd3553b490053829676d47.png)
Escribe como varias potencias:
- 47)
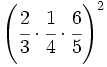
- 48)
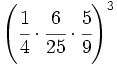
- 49)
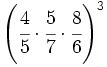
- 50)
![\left[ \cfrac{1}{3} \cdot \left( \cfrac{-2~}{5} \right) \cdot \left( \cfrac{-2~}{2} \right) \right]^2](/wikipedia/images/math/5/b/1/5b1a30cdfd3990559ce215699a00c2e3.png)
- 51)
![\left[ \cfrac{2}{3} \cdot \left( \cfrac{-5~}{4} \right) \cdot \cfrac{8}{5} \cdot \left( \cfrac{-5~}{2} \right) \right]^{-3}](/wikipedia/images/math/4/0/6/4066e6d3414c3e8d17a4b0e6837cad6a.png)
Escribe como una sola potencia:
- 52)
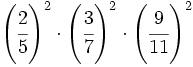
- 53)
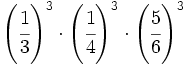
- 55)
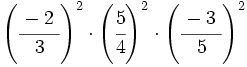
- 56)
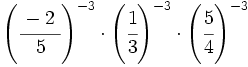
- 57)
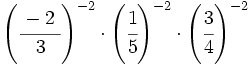
- 58)
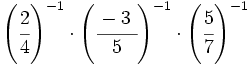
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 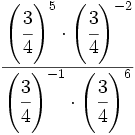
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Cálculos con potencias dentro de fracciones:
Calcula:
- 59)
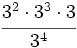
- 60)
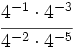
- 61)
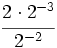
- 62)
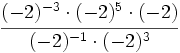
Calcula:
- 63)
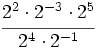
- 64)
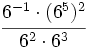
- 65)
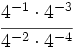
- 66)
![\cfrac{(-3)^{-2} \cdot (-3)^{-3}}{\left[ (-3)^2 \right]^{-2}}\;](/wikipedia/images/math/5/e/b/5eb0dbb75ab3ac5de8238f112e4d893f.png)
Simplifica: 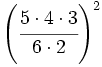
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 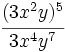
Simplifica: 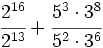
Simplifica y expresa la solución como una única potencia:
a) 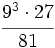
b) 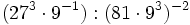
c) 
d) 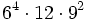
e) a) 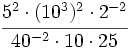
Simplifica y expresa la solución como una única potencia:
a) 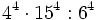
b) 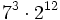
c) 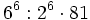
d) 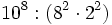
e) 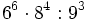
f) 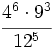
Simplifica:
- a)
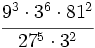
- b)
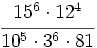
Simplifica:
- a)
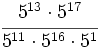
- b)
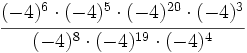
- c)
![\left[ \cfrac{( 2^3 \cdot 2^6)^{-2} \cdot (3^4)^3 \cdot 3 }{( 2^6 \cdot 2^{10})^{-1}\cdot (3^6 \cdot 3^2 \cdot 3^5)}\right]^{10}](/wikipedia/images/math/c/8/5/c85c926802bdbb7a51ef34eb65c6dda7.png)
Cálculos de diversos tipos:
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Exponente positivo:
- a)
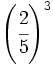 ; b)
; b)  ; c)
; c)  ; d)
; d) 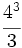 ; e)
; e) 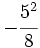
Exponente negativo:
- f)
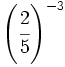 ; g)
; g) 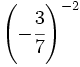 ; h)
; h) 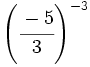 ; i)
; i) 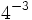 ; j)
; j) 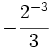
Operaciones combinadas:
- k)
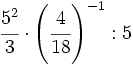 ; l)
; l)