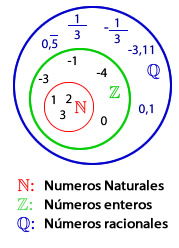
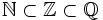Plantilla:El conjunto de los números racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:10 30 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:20 20 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| }} | }} | ||
| - | *Todos los números decimales exactos o periódicos se pueden expresar en forma de fracción. | + | *Todos los números decimales exactos o periódicos se pueden expresar en forma de fracción. Por tanto, son números racionales. |
| *Cuando el número de decimales es infinito y no periódico, como ocurre con el número pi <math>(\pi)</math>, no podemos expresarlo en forma de fracción. A estos números los llamaremos '''irracionales'''.}} | *Cuando el número de decimales es infinito y no periódico, como ocurre con el número pi <math>(\pi)</math>, no podemos expresarlo en forma de fracción. A estos números los llamaremos '''irracionales'''.}} | ||
| }} | }} | ||
Revisión de 13:20 20 nov 2017
El conjunto de los números racionales es el conjunto de todas las fracciones: 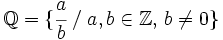 Propiedades
|