Plantilla:Relación de proporcionalidad inversa 1ºESO
De Wikipedia
| Revisión de 17:16 4 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | + | {{Caja_Amarilla|texto=Dos [[El Sistema Métrico Decimal (1º ESO)|magnitudes]] son '''inversamente proporcionales''' cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda dividida (resp. multiplicada) por el mismo número. | |
| - | {{Caja_Amarilla|texto=Dos magnitudes son '''inversamente proporcionales''' cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda dividida (resp. multiplicada) por el mismo número. | + | }} |
| + | {{p}} | ||
| + | {{Warning|titulo=Advertencia|texto=Es muy común pensar que dos magnitudes son inversamente proporcionales si al aumentar (resp. disminuir) una de ellas, disminuye (resp. aumenta) la otra. No es exactamente así. No es suficiente con que disminuya (resp. aumente) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se divide (resp. multiplica) la otra, por el mismo número. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 27: | Línea 29: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_angelmartinez | ||
| + | |titulo1=Magnitudes inversamente proporcionales | ||
| + | |duracion=3'10" | ||
| + | |sinopsis=Magnitudes inversamente proporcionales. Razón de proporcionaledad inversa. | ||
| + | |url1=https://www.youtube.com/watch?v=XKBi-Qz5xhw | ||
| + | }} | ||
| + | {{Actividades|titulo=Magnitudes inversamente proporcionales|enunciado= | ||
| + | {{AI_melide | ||
| + | |titulo1=Autoevaluación 1 | ||
| + | |descripcion=Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales. | ||
| + | |url1=http://maralboran.org/web_ma/Melide/Razon_y_proporcion/Magnitudes%20inversamente%20proporcionales.html | ||
| + | }} | ||
| {{AI_vitutor | {{AI_vitutor | ||
| - | |titulo1=Autoevaluación: ''Magnitudes inversamente proporcionales'' | + | |titulo1=Autoevaluación 2 |
| |descripcion=Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales. | |descripcion=Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales. | ||
| |url1=http://www.vitutor.com/di/p/a_8e.html | |url1=http://www.vitutor.com/di/p/a_8e.html | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| ===Constante de proporcionalidad inversa=== | ===Constante de proporcionalidad inversa=== | ||
| - | {{Teorema_sin_demo|titulo=Propiedad|enunciado=Al multiplicar dos magnitudes inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina '''constante de proporcionalidad inversa'''.}} | + | {{Teorema_sin_demo|titulo=Propiedad|enunciado=Al multiplicar dos [[El Sistema Métrico Decimal (1º ESO)|magnitudes]] inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina '''constante de proporcionalidad inversa'''.}} |
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| Línea 65: | Línea 80: | ||
| {{p}} | {{p}} | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Relación de proporcionalidad inversa | + | |titulo1=Constante de proporcionalidad inversa |
| |descripcion=Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa. | |descripcion=Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa. | ||
Revisión actual
Dos magnitudes son inversamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda dividida (resp. multiplicada) por el mismo número.
Es muy común pensar que dos magnitudes son inversamente proporcionales si al aumentar (resp. disminuir) una de ellas, disminuye (resp. aumenta) la otra. No es exactamente así. No es suficiente con que disminuya (resp. aumente) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se divide (resp. multiplica) la otra, por el mismo número.
El número de obreros que trabajan en una construcción y el tiempo que tardan en finalizarla son magnitudes inversamente proporcionales, ya que si el número de obreros es el doble (o el triple,...), el tiempo que tardan será la mitad (o la tercera parte, ...).
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
Magnitudes inversamente proporcionales. Razón de proporcionaledad inversa.
Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales.
Ejercicios de autoevaluación sobre magnitudes inversamente proporcionales.
Constante de proporcionalidad inversa
Propiedad
Al multiplicar dos magnitudes inversamente proporcinales siempre se obtiene el mismo valor. A dicho valor se le denomina constante de proporcionalidad inversa.
En el ejemplo anterior, en el que relacionabamos el número de obreros y el tiempo que tardan en finalizar una obra
Número de obreros |
2 |
4 |
10 |
20 |
Tiempo que tardan (horas) |
20 |
10 |
4 |
2 |
se observa que:
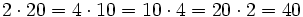
Actividades para que aprendas y practiques el cálculo de la constante de proporcionalidad inversa y sus uso para resolver problemas de proporcionalidad inversa.

