Plantilla:Polinomios
De Wikipedia
| Revisión de 09:20 5 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:33 22 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| }} | }} | ||
| }} | }} | ||
| - | {{Caja_Amarilla|texto= | + | {{Tabla50|celda2=[[Imagen:polinomio.gif|thumb|elementos y grado de un polinomio]] |
| + | |celda1={{Caja_Amarilla|texto= | ||
| *Un '''polinomio''' es una expresión algebraica que se obtiene al sumar dos o más monomios. A cada monomio se le llama '''término''' del polinomio. Si tiene dos términos se llama '''binomio'''; si tiene tres '''trinomio'''; si tiene cuatro '''cuatrinomio''' etc. Se nombran con letras mayúsculas, seguidas de unos paréntesis que contienen las letras de la parte literal, separadas por comas: P(x), Q(x,y), ... | *Un '''polinomio''' es una expresión algebraica que se obtiene al sumar dos o más monomios. A cada monomio se le llama '''término''' del polinomio. Si tiene dos términos se llama '''binomio'''; si tiene tres '''trinomio'''; si tiene cuatro '''cuatrinomio''' etc. Se nombran con letras mayúsculas, seguidas de unos paréntesis que contienen las letras de la parte literal, separadas por comas: P(x), Q(x,y), ... | ||
| *Un polinomio se dice que es '''nulo''' si todos los monomios que lo componen tienen coeficiente cero. | *Un polinomio se dice que es '''nulo''' si todos los monomios que lo componen tienen coeficiente cero. | ||
| Línea 29: | Línea 30: | ||
| *Dos polinomios son '''iguales''' si al reducirlos los coeficientes de los monomios con la misma parte literal, en uno y en otro polinomio, son '''iguales''', aunque estén en distinto orden. | *Dos polinomios son '''iguales''' si al reducirlos los coeficientes de los monomios con la misma parte literal, en uno y en otro polinomio, son '''iguales''', aunque estén en distinto orden. | ||
| *Dos polinomios son '''semejantes''' si los monomios no nulos que los componen tienen la misma parte literal en uno y otro polinomio. | *Dos polinomios son '''semejantes''' si los monomios no nulos que los componen tienen la misma parte literal en uno y otro polinomio. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:33 22 nov 2017
Los siguientes videotutoriales condensan los conceptos que vamos a ver en este apartado sobre polinomios.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos. Valor numérico de un polinomio.
|
a) El polinomio 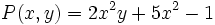 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
b) El polinomio 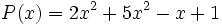 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 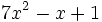 . Es de grado 2.
. Es de grado 2.
c) Los polinomios constantes, como por ejemplo 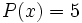 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 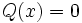 , tiene grado cero.
, tiene grado cero.
d) Los polinomios 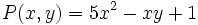 y
y 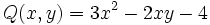 son semejantes.
son semejantes.
e) Los polinomios 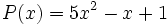 y
y 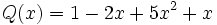 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes...
Polinomios. Grado de un polinomio. Ejemplos.
Polinomios. Grado de un polinomio. Ejemplos.
Aprende a calcular el grado relativo y absoluto de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
- a)
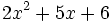
- b)
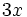
- c)
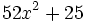
- d)
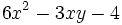
- e)
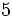
- f)
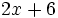
2) Expresa en forma reducida los siguientes polinomios:
- a)
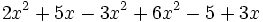
- b)
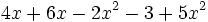
- c)
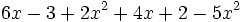
- d)
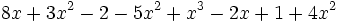
3) Indica el grado de cada polinomio:
- a)
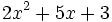 ; b)
; b) 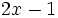 ; c)
; c) 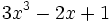
- d)
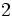 ; e)
; e) 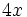 ; f)
; f) 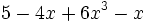
- g)
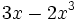 ; h)
; h) 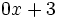 ; i)
; i) 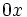
4) Indica cuáles de estos polinomios son iguales:
- a)
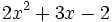 ; b)
; b) 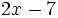 ; c)
; c) 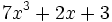 ; d)
; d) 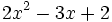
- e)
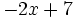 ; f)
; f) 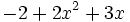 ; g)
; g) 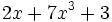 ; h)
; h) 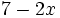
- i)
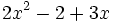 ; j)
; j) 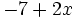 ; k)
; k) 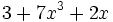 ; l)
; l) 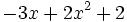
5) Indica cuáles de estos polinomios son semejantes entre sí:
- a)
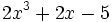 ; b)
; b) 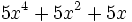 ; c)
; c) 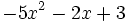
- d)
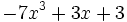 ; e)
; e) 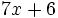 ; f)
; f) 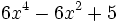
- g)
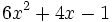 ; h)
; h) 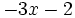
2) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
- a)
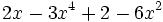
- b)
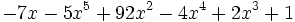
- c)
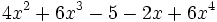
- d)
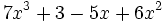
- e)
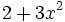
- f)
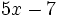
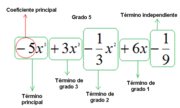
Elementos y grado de un polinomio.
Expresiones algebraicas: monomios y polinomios.
- Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación.
- Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos.
- Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio.
- Actividad en la que aprenderás a escribir polinomios en su forma usual.
- Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio.