Plantilla:Def division
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:38 7 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace_sensei | ||
| - | |titulo1=Multiplicación de números naturales. Propiedades | ||
| - | |duracion=9'54" | ||
| - | |sinopsis=Videotutorial que resume lo que vamos a ver en este apartado sobre multiplicación de números naturales y sus propiedades. | ||
| - | |url1=https://www.youtube.com/watch?v=JvheD8VqBhA&list=PLA0brQx7U3OVuqlFgdMawKu5TtMwqCbH5&index=3 | ||
| - | }} | ||
| - | {{p}} | ||
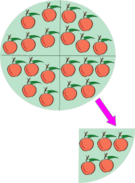
| {{Tabla75|celda2=[[Imagen:divide20by4.png|thumb|center|135px|<math>20 : 4=5</math>]]|celda1={{Caja_Amarilla|texto=Sean <math>D\;</math> y <math>d\;</math> dos números naturales, con <math>d \ne 0</math>. | {{Tabla75|celda2=[[Imagen:divide20by4.png|thumb|center|135px|<math>20 : 4=5</math>]]|celda1={{Caja_Amarilla|texto=Sean <math>D\;</math> y <math>d\;</math> dos números naturales, con <math>d \ne 0</math>. | ||
| Línea 14: | Línea 7: | ||
| *Vamos a distinguir dos casos: | *Vamos a distinguir dos casos: | ||
| **Si <math>d\;</math> está contenido en <math>D\;</math> un número "exacto" de veces (el cociente, <math>c\;</math>, es un número natural tal que <math>D=d \cdot c\;</math>), diremos que la división es '''exacta'''. | **Si <math>d\;</math> está contenido en <math>D\;</math> un número "exacto" de veces (el cociente, <math>c\;</math>, es un número natural tal que <math>D=d \cdot c\;</math>), diremos que la división es '''exacta'''. | ||
| - | **En caso contrario diremos que la división '''es entera'''. Si ocurre esto, es posible encontrar un número natural <math>r\;</math>, lo más pequeño posible, de manera que si se lo restamos al dividendo, <math>D\;</math>, y dividimos el resultado por el divisor, <math>d\;</math>, la división es exacta. A dicho número <math>r\;</math>, lo llamaremos '''resto''' o '''residuo''' de la división. | + | **En caso contrario diremos que la división '''es entera'''. Si ocurre esto, es posible encontrar un número natural <math>r\;</math>, menor que <math>d\;</math>, de manera que si dividimos <math>D-r\;</math> entre <math>d\;</math>, la división es exacta. A dicho número <math>r\;</math> lo llamaremos '''resto''' o '''residuo''' de la división. |
| }} | }} | ||
| }} | }} | ||
Revisión actual
Sean
|  |
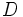y 
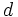dos números naturales, con 
.
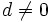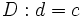
, cociente.
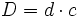), diremos que la división es exacta.
, menor que 
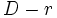entre 
