Plantilla:Números compuestos y números primos

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión actual

Un número primo es un número natural, mayor que 1, que sólo tiene dos divisores: él mismo y el 1.
Un número es compuesto si tiene más de dos divisores.

Propiedad

Un número compuesto puede ponerse como producto de dos números distintos de él y la unidad.
Este proceso se puede repetir, con cada uno de los factores, hasta que el número quede descompuesto en producto de factores primos. A esto se le llama descomponer un número en factores primos.

Ejemplos

15 es compuesto porque 15 = 3·5.
El número 2 es primo ya que sus únicos divisores son 1 y 2. También son primos: 3, 5, 7, 11, 13.

Números primos y compuestos

Tutorial 1 (2´41") Sinopsis:

Conceptos de número primo y número compuesto. Tabla de números primos menores que 100.

Tutorial 2 (2´22") Sinopsis:

Conceptos de número primo y número compuesto.

Tutorial 3 (11´47") Sinopsis:

Conceptos de número primo y número compuesto.

Tutorial 4 (6´19") Sinopsis:

Breve explicación de qué son los números primos, cómo reconocerlos y cómo encontrarlos fácilmente

Tutorial 5 (9´30") Sinopsis:

Conceptos de número primo y número compuesto. Criba de Eratóstenes.

Tutorial 6 (8´49") Sinopsis:

Números primos.

La división y los números primos (9'12") Sinopsis:

The building blocks of all natural numbers are the prime numbers. The early Greeks invented the system still used today for separating natural numbers into prime and composite numbers.

(Disponibles los subtítulos en inglés)

Números naturales. Números primos (17´) Sinopsis:

Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)

Ejercicio (6´57") Sinopsis:

Determina cuáles de los siguientes números son primos, cuáles son compuestos, y cuáles no son ni primos ni compuestos:

24, 2, 1 y 17.

Números primos menores que 100

Actividades: Números primos y compuestos

Actividad 1 Descripción:

Actividad en la que puedes ver si un número es primo o compuesto.
Actividad en la que debes separar los números primos de los compuestos.

Actividad 2 Descripción:

Actividad 3 Descripción:

Introducción a los números primos y compuestos.

Actividad 4 Descripción:

Repaso sobre números primos y compuestos.

Actividad 5 Descripción:

Actividad en la que aprenderás a determinar si un número es primo o compuesto.

Actividad 6 Descripción:

Actividad en la que deberás decidir si un número es primo o compuesto.

Actividad 7 Descripción:

Actividad en la que deberás decidir si un número es primo o compuesto.

Actividad 8 Descripción:

Actividad en la que deberás pulsar sobre los números primos.

Autoevaluación 1 Descripción:

Identifica números primos.

Autoevaluación 2 Descripción:

Identifica números compuestos.

Autoevaluación 3 Descripción:

Test de 10 preguntas sobre números primos y compuestos.

Autoevaluación 4 Descripción:

Ejercicios de autoevaluación sobre números primos.

Autoevaluación 5 Descripción:

Ejercicios de autoevaluación sobre números compuestos.

[editar]

Criba de Eratóstenes

La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado n, que desarrolló el célebre matemático griego Eratóstenes en el siglo III a.C.

Procedimiento

Se forma una tabla con todos los números naturales comprendidos entre 2 y n, y se van tachando los números que no son primos de la siguiente manera:

Comenzando por el 2, se tachan todos sus múltiplos.
Comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente.
El proceso termina cuando el cuadrado del mayor número declarado como primo es mayor que n. Tras haber tachado sus múltiplos, los número que quedan sin tachar son todos los primos entre 2 y n.

Animación de la criba de Eratóstenes para números primos menores que 120. Se incluye la optimización de comenzar por los cuadrados de números primos.

Determinemos, mediante el siguiente ejemplo, el proceso para determinar la lista de los números primos menores de 20.

Primer paso: listar los números naturales comprendidos entre 2 y 20.

2. Segundo paso: Se toma el primer número no rayado ni marcado, como número primo.

3. Tercer paso: Se tachan todos los múltiplos del número que se acaba de indicar como primo.

4. Cuarto paso: Si el cuadrado del primer número que no ha sido rayado ni marcado es inferior a 20, entonces se repite el segundo paso. Si no, el algoritmo termina, y todos los enteros no tachados son declarados primos.

Como 3² = 9 < 20, se vuelve al segundo paso:

5. Quinto paso: En el cuarto paso, el primer número que no ha sido tachado ni marcado es 5. Se tachan sus múltiplos. Como su cuadrado es mayor que 20, el algoritmo termina y se consideran primos todos los números que no han sido tachados.

Como resultado se obtienen los números primos comprendidos entre 2 y 20, y estos son: 2, 3, 5, 7, 11, 13, 17, 19.

Criba de Eratóstenes (7´38") Sinopsis:

Determinación de los números primos utilizando la Criba de Eratóstenes.

Optimización del método:

Al seguir este método de búsqueda de primos, cada vez que marcamos un número como primo, no es necesario empezar a buscar sus múltiplos desde el más pequeño, sino desde su cuadrado, pues todos los anteriores ya habrían sido eliminados por ser múltiplos de primos más pequeños.

Criba de Eratóstenes

Criba de Eratóstenes Descripción:

En esta escena podrás practicar el procedimiento de la criba de Eratóstenes para obtener números primos.

Criba de Eratóstenes Descripción:

Actividad para practicar la criba de Eratóstenes.

[editar]

Cómo averiguar si un número es primo

Procedimiento para ver si un número es primo

Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).

Ejemplo: Averiguar si un número es primo

Averigua si el número 167 es primo.

Solución:

Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7, 11, 13, 17,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:

167 : 2 $\rightarrow$ (cociente=83, resto=1) No es divisible por 2. Como 83>3 sigo probando con 3.

167 : 3 $\rightarrow$ (cociente=55, resto=2) No es divisible por 3. Como 55>5 sigo probando con 5.

167 : 5 $\rightarrow$ (cociente=33, resto=2) No es divisible por 5. Como 33>7 sigo probando con 7.

167 : 7 $\rightarrow$ (cociente=23, resto=6) No es divisible por 7. Como 23>11 sigo probando con 11.

167 : 11 $\rightarrow$ (cociente=15, resto=2) No es divisible por 11. Como 15>13 sigo probando con 13.

167 : 13 $\rightarrow$ (cociente=12, resto=11) No es divisible por 13. Como 12<17 paro.

Por tanto, 167 es primo.

Averiguar si un número es primo

Ejercicio 1 (6´54") Sinopsis:

Números primos y compuestos.
Averigua si son primos o compuestos los siguientes números: 263, 137 y 119.

Ejercicio 2 (13´47") Sinopsis:

Averigua si son primos o compuestos los siguientes números: 43, 293 y 611.

Números primos

Actividad: Números primos y compuestos

a) ¿Es 63 un número primo?

b) ¿Es 181 un número primo?

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) is 63 a prime number?

b) is 181 a prime number?

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:N%C3%BAmeros_compuestos_y_n%C3%BAmeros_primos"

-{{Tabla75|
+{{def numeros primos y compuestos}}
-celda1=
-{{p}}{{Caja_Amarilla|texto=
-Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}}<br>
-{{Ejemplo_simple|titulo=Ejemplos|contenido=
-*15 es compuesto porque <math>15=3 \cdot 5</math>.
-*Los números 2, 3, 5, 7, 11, 13 son primos.}}
 {{p}}
-{{Caja Amarilla|texto=
+===Criba de Eratóstenes===
-'''Propiedad:''' Un número primo sólo tiene por divisores a la unidad y a él mismo.}}
+{{tabla50|celda1=
-|celda2=
+{{Caja_Amarilla|texto=
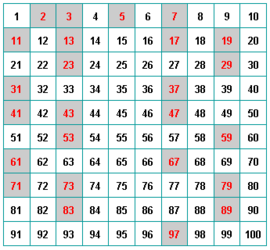
-[[Imagen:tabla_primos.png|center|thumb|Números primos menores que 100]]
+La '''criba de Eratóstenes''' es un algoritmo que permite hallar todos los números primos menores que un número natural dado ''n'', que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C.
 }}
 {{p}}
-{{Video2
+{{Teorema_sin_demo|titulo=Procedimiento|enunciado=
-|titulo1=Números naturales. Números primos
+Se forma una tabla con todos los números naturales comprendidos entre 2 y ''n'', y se van tachando los números que no son primos de la siguiente manera:
-|duracion=17´
+*Comenzando por el 2, se tachan todos sus múltiplos.
-|sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos
+*Comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente.
-números?...   Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.
+*El proceso termina cuando el cuadrado del mayor número declarado como primo es mayor que ''n''. Tras haber tachado sus múltiplos, los número que quedan sin tachar son todos los primos entre 2 y ''n''.
-|url1=http://maralboran.org/web_ma/videos/naturales/naturales.htm
 }}
 {{p}}
-===Criba de Eratóstenes===
+|celda2=
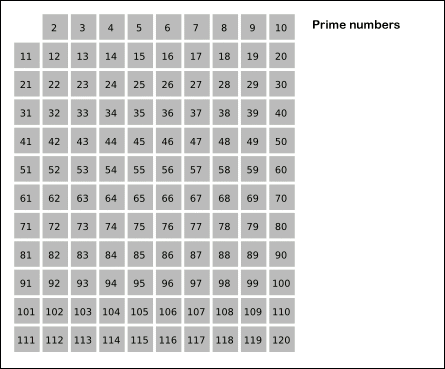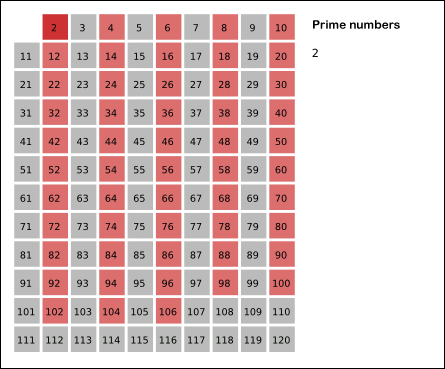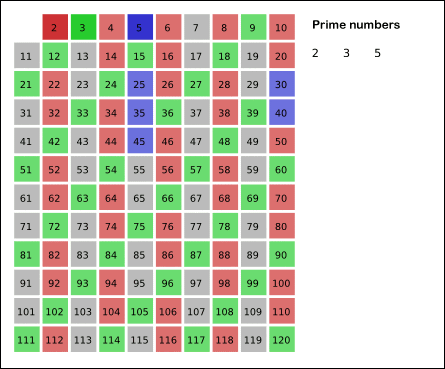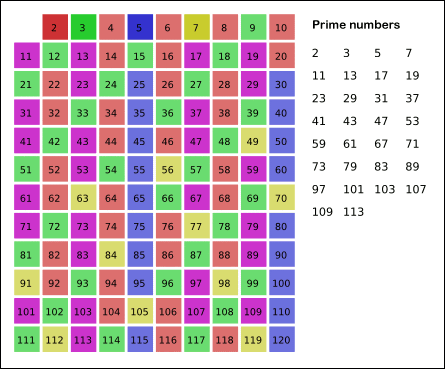
-La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C.
+[[Imagen:criba_eratostenes.gif|thumb|450px|Animación de la criba de Eratóstenes para números primos menores que 120. Se incluye la optimización de comenzar por los cuadrados de números primos.]]
-<br>
+}}
 {{p}}
-===Cómo averiguar si un número es primo===
+Determinemos, mediante el siguiente ejemplo, el proceso para determinar la lista de los números primos menores de 20.
-Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).
+#''Primer paso'': listar los números naturales comprendidos entre 2 y 20.
+<center>
+{| border="1" cellspacing="0" cellpadding="2"
+|-----
+| bgcolor="#d1c4ad" |  2 || bgcolor="#d1c4ad" |  3
+| bgcolor="#d1c4ad" |  4
+| bgcolor="#d1c4ad" |  5 || bgcolor="#d1c4ad" |  6
+| bgcolor="#d1c4ad" |  7
+| bgcolor="#d1c4ad" |  8 || bgcolor="#d1c4ad" |  9
+| bgcolor="#d1c4ad" | 10
+| bgcolor="#d1c4ad" | 11 || bgcolor="#d1c4ad" | 12
+| bgcolor="#d1c4ad" | 13
+| bgcolor="#d1c4ad" | 14 || bgcolor="#d1c4ad" | 15
+| bgcolor="#d1c4ad" | 16
+| bgcolor="#d1c4ad" | 17 || bgcolor="#d1c4ad" | 18
+| bgcolor="#d1c4ad" | 19 || bgcolor="#d1c4ad" | 20
+|}
+</center>
+:2. ''Segundo paso'': Se toma el primer número no rayado ni marcado, como número primo.
+<center>
+{| border="1" cellspacing="0" cellpadding="2"
+|-----
+| bgcolor="#ff0000" |  2 || bgcolor="#d1c4ad" |  3
+| bgcolor="#d1c4ad" |  4
+| bgcolor="#d1c4ad" |  5 || bgcolor="#d1c4ad" |  6
+| bgcolor="#d1c4ad" |  7
+| bgcolor="#d1c4ad" |  8 || bgcolor="#d1c4ad" |  9
+| bgcolor="#d1c4ad" | 10
+| bgcolor="#d1c4ad" | 11 || bgcolor="#d1c4ad" | 12
+| bgcolor="#d1c4ad" | 13
+| bgcolor="#d1c4ad" | 14 || bgcolor="#d1c4ad" | 15
+| bgcolor="#d1c4ad" | 16
+| bgcolor="#d1c4ad" | 17 || bgcolor="#d1c4ad" | 18
+| bgcolor="#d1c4ad" | 19 || bgcolor="#d1c4ad" | 20
+|}
+</center>
+:3. ''Tercer paso'': Se tachan todos los múltiplos del número que se acaba de indicar como primo.
+<center>
+{| border="1" cellspacing="0" cellpadding="2"
+|-----
+| bgcolor="#ff0000" |  2 || bgcolor="#d1c4ad" |  3
+| <span style="color:#ff0000;text-decoration:line-through;"> 4 </span>
+| bgcolor="#d1c4ad" |  5
+| <span style="color:#ff0000;text-decoration:line-through;"> 6 </span>
+| bgcolor="#d1c4ad" |  7
+| <span style="color:#ff0000;text-decoration:line-through;"> 8 </span>
+| bgcolor="#d1c4ad" |  9
+| <span style="color:#ff0000;text-decoration:line-through;"> 10 </span>
+| bgcolor="#d1c4ad" |  11
+| <span style="color:#ff0000;text-decoration:line-through;"> 12 </span>
+| bgcolor="#d1c4ad" |  13
+| <span style="color:#ff0000;text-decoration:line-through;"> 14 </span>
+| bgcolor="#d1c4ad" |  15
+| <span style="color:#ff0000;text-decoration:line-through;"> 16 </span>
+| bgcolor="#d1c4ad" |  17
+| <span style="color:#ff0000;text-decoration:line-through;"> 18 </span>
+| bgcolor="#d1c4ad" |  19
+| <span style="color:#ff0000;text-decoration:line-through;"> 20 </span>
+|}
+</center>
+:4. ''Cuarto paso'': Si el cuadrado del primer número que no ha sido rayado ni marcado es inferior a 20, entonces se repite el segundo paso. Si no, el algoritmo termina, y todos los enteros no tachados son declarados primos.
+:Como 3² = 9 < 20, se vuelve al segundo paso:
+<center>
+{| border="1" cellspacing="0" cellpadding="2"
+|-----
+| bgcolor="#ff0000" |  2 || bgcolor="#0000ff" |  3
+| <span style="color:#ff0000;text-decoration:line-through;"> 4 </span>
+| bgcolor="#d1c4ad" |  5
+| <span style="color:#ff0000;text-decoration:line-through;"> 6 </span>
+| bgcolor="#d1c4ad" |  7
+| <span style="color:#ff0000;text-decoration:line-through;"> 8 </span>
+| <span style="color:#0000ff;text-decoration:line-through;"> 9 </span>
+| <span style="color:#ff0000;text-decoration:line-through;"> 10 </span>
+| bgcolor="#d1c4ad" |  11
+| <span style="color:#ff0000;text-decoration:line-through;"> 12 </span>
+| bgcolor="#d1c4ad" |  13
+| <span style="color:#ff0000;text-decoration:line-through;"> 14 </span>
+| <span style="color:#0000ff;text-decoration:line-through;"> 15 </span>
+| <span style="color:#ff0000;text-decoration:line-through;"> 16 </span>
+| bgcolor="#d1c4ad" |  17
+| <span style="color:#ff0000;text-decoration:line-through;"> 18 </span>
+| bgcolor="#d1c4ad" |  19
+| <span style="color:#ff0000;text-decoration:line-through;"> 20 </span>
+|}
+</center>
+:5. ''Quinto paso:'' En el cuarto paso, el primer número que no ha sido tachado ni marcado es 5. Se tachan sus múltiplos. Como su cuadrado es mayor que 20, el algoritmo termina y se consideran primos todos los números que no han sido tachados.
+:Como resultado se obtienen los números primos comprendidos entre 2 y 20, y estos son: 2, 3, 5, 7, 11, 13, 17, 19.
+{{p}}
+{{Video_enlace
+|titulo1=Criba de Eratóstenes
+|duracion=7´38"
+|url1=http://www.youtube.com/watch?v=bNMeeMsnvK8
+|sinopsis=Determinación de los números primos utilizando la Criba de Eratóstenes.
+}}
+{{p}}
+{{Nota|titulo=Optimización del método:|texto= Al seguir este método de búsqueda de primos, cada vez que marcamos un número como primo, no es necesario empezar a buscar sus múltiplos desde el más pequeño, sino desde su cuadrado, pues todos los anteriores ya habrían sido eliminados por ser múltiplos de primos más pequeños.
+}}
+{{Actividades|titulo=Criba de Eratóstenes|enunciado=
+{{Geogebra_enlace
+|descripcion=En esta escena podrás practicar el procedimiento de la criba de Eratóstenes para obtener números primos.
+|enlace=[http://ggbm.at/fbreeTrC Criba de Eratóstenes]
+}}
+{{AI_cidead
+|titulo1=Criba de Eratóstenes
+|descripcion=Actividad para practicar la criba de Eratóstenes.
+|url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena2/1quincena2_contenidos_2b.htm
+}}
+}}
+===Cómo averiguar si un número es primo===
+{{Teorema_sin_demo|titulo=Procedimiento para ver si un número es primo|enunciado=
+Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).}}
+{{p}}
 {{Ejemplo
 |titulo=Ejemplo: ''Averiguar si un número es primo''
 |enunciado=
-:Averigua si el número 167 es primo.
+Averigua si el número 167 es primo.
 |sol=
-Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:<br>
+Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7, 11, 13, 17,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:<br>
-:Dividimos 167 entre 2: cociente=83 y resto=1. No es divisible por 2.
+:167 : 2 <math>\rightarrow</math> (cociente=83, resto=1) No es divisible por 2. Como 83>3 sigo probando con 3.
-:Dividimos 167 entre 3 porque 83>3: cociente=55 y resto=2. No es divisible por 3.
+:167 : 3 <math>\rightarrow</math> (cociente=55, resto=2) No es divisible por 3. Como 55>5 sigo probando con 5.
-:Dividimos 167 entre 5 porque 55>5: cociente=33 y resto=2. No es divisible por 5.
+:167 : 5 <math>\rightarrow</math> (cociente=33, resto=2) No es divisible por 5. Como 33>7 sigo probando con 7.
-:Dividimos 167 entre 7 porque 33>7: cociente=23 y resto=6. No es divisible por 7.
+:167 : 7 <math>\rightarrow</math> (cociente=23, resto=6) No es divisible por 7. Como 23>11 sigo probando con 11.
-:Dividimos 167 entre 11 porque 23>11: cociente=15 y resto=2. No es divisible por 11.
+:167 : 11 <math>\rightarrow</math> (cociente=15, resto=2) No es divisible por 11. Como 15>13 sigo probando con 13.
-:Dividimos 167 entre 13 porque 15>13: cociente=12 y resto=11. No es divisible por 13.
+:167 : 13 <math>\rightarrow</math> (cociente=12, resto=11) No es divisible por 13. Como 12<17 paro.
-:Paramos y no dividimos 167 entre 17 porque 12<17.<br>
 Por tanto, 167 es primo.
 }}
 {{p}}
-{{wolfram
+{{Videotutoriales|titulo=Averiguar si un número es primo|enunciado=
-|titulo=Actividad: ''Números primos y compuestos''
+{{Video_enlace_tutomate
-|cuerpo=
+|titulo1=Ejercicio 1
-{{ejercicio_cuerpo
+|duracion=6´54"
-|enunciado=
+|url1=https://www.youtube.com/watch?v=8fIExtr_Nkk&index=3&list=PLWRbPOo5oaTdkjULDYWW9nD0VBzgmf239
+|sinopsis=*Números primos y compuestos.
-:a) ¿Es 63 un número primo?
+*Averigua si son primos o compuestos los siguientes números: 263, 137 y 119.
-:b) ¿Es 181 un número primo?
-{{p}}
-|sol=
-Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
-:a) {{consulta|texto=is 63 a prime number?}}
-:a) {{consulta|texto=is 181 a prime number?}}
-{{widget generico}}
 }}
+{{Video_enlace_math2me
+|titulo1=Ejercicio 2
+|duracion=13´47"
+|url1=https://www.youtube.com/watch?v=UJbKeig7GFI
+|sinopsis=Averigua si son primos o compuestos los siguientes números: 43, 293 y 611.
+}}
+}}
+{{p}}
+{{wolfram desplegable|titulo=Números primos|contenido=
+{{wolfram numeros primos}}
 }}
 {{p}}

Plantilla:Números compuestos y números primos

De Wikipedia

Revisión actual

Criba de Eratóstenes

Cómo averiguar si un número es primo

Vistas

Herramientas personales

Menú

Buscar

Herramientas