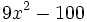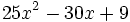Identidades
De Wikipedia
| Revisión de 08:30 28 abr 2009 Coordinador (Discusión | contribuciones) (→Identidades notables) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| - | |repasar=[[Algebra(1º ESO)|Algebra (1º ESO)]] | + | |repasar= |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| ==Identidad== | ==Identidad== | ||
| - | {{Caja_Amarilla|texto= | + | {{identidad}} |
| - | *Una '''identidad''' es una expresión algebraica, en forma de igualdad, que es cierta para cualquier valor que le demos a las letras que intervienen. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ==Identidades notables== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | *'''Cuadrado de una suma:''' <math>(a + b)^2 = a^2 + 2ab + b^2 \;\!</math> | ||
| - | {{Desplegable|titulo={{b4}}|contenido= | ||
| - | :Demostración visual: | ||
| - | <center><iframe> | + | ==Productos notables== |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/cuadrado_suma.html | + | {{identidades notables}} |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/cuadrado_suma.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | *'''Cuadrado de una diferencia:''' <math>(a - b)^2 = a^2 - 2ab + b^2 \;\!</math> | + | |
| - | {{Desplegable|titulo={{b4}}|contenido= | + | |
| - | :Demostración visual: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/cuadrado_diferencia.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/cuadrado_diferencia.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | *'''Suma por diferencia:''' <math>(a + b) (a-b) = a^2 - b^2 \;\!</math> | + | |
| - | {{Desplegable|titulo={{b4}}|contenido= | + | |
| - | Demostración visual: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/suma_por_diferencia.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/suma_por_diferencia.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | + | ==Factorización de polinomios usando productos notables== | |
| - | {{Ejemplo | + | {{factorización de polinomios usando identidades notables}} |
| - | |titulo=Ejemplos: ''Identidades notables'' | + | |
| - | |enunciado= | + | |
| - | :Calcula: | + | |
| - | ::a) <math>(5x-2)^2 \;\!</math> | + | |
| - | ::b) <math>(2x-3)(2x+3) \;\!</math> | + | |
| - | + | ||
| - | |sol= | + | |
| - | ::a) <math>(5x-2)^2 = (5x)^2-2 \cdot (5x) \cdot 2+2^2=25x^2-20x+4 \;\!</math> | + | |
| - | ::b) <math>(2x-3)(2x+3)=(2x)^2-3^2=4x^2-9 \;\!</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Identidades notables''|cuerpo= | + | ==Ejercicios== |
| - | {{ai_cuerpo | + | {{Ejercicios: Identidades notables}} |
| - | |enunciado='''Actividad 1:''' Ejercicios de autoevaluación sobre identidades notables. | + | |
| - | |actividad= | + | |
| - | <center><iframe> | ||
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayerP3V?p3v=true&xref=200412020906_AC_0_-1727884769&mode=1&rtc=1001&locale=es&cache=false | ||
| - | width=100% | ||
| - | height=620 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayerP3V?p3v=true&xref=200412020906_AC_0_-1727884769&mode=1&rtc=1001&locale=es&cache=false '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ===Factorización de polinomios usando identidades notables=== | ||
| - | Mediante identidades notables podemos transformar un polinomio en un producto de factores. | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejemplos: ''Factorización de polinomios usando identidades notables'' | ||
| - | |enunciado= | ||
| - | :Factoriza: | ||
| - | ::a) <math>4x^2-9 \;\!</math> | ||
| - | ::b) <math>x^2+4x+4 \;\!</math> | ||
| - | |||
| - | |sol= | ||
| - | ::a) <math>4x^2-9=(2x+3)(2x-3) \;\!</math> | ||
| - | ::b) <math>x^2+4x+4 = (x+2)^2\;\!</math> | ||
| - | }} | ||
| - | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Identidad
- Una identidad es una expresión algebraica, en forma de igualdad, que es cierta para cualquier valor que le demos a las letras que intervienen.
Productos notables
Los productos notables son unas identidades de ciertos productos de binomios que resultan útiles para abreviar los cálculos con expresiones algebraicas.
Productos notables
- Cuadrado de una suma:
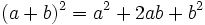
- Cuadrado de una diferencia:

- Suma por diferencia:
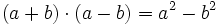
- Cuadrado de una suma:
Escena que demuestra geométricamente la fórmula del cuadrado de una suma
- Cuadrado de una diferencia:
Escena que demuestra geométricamente la fórmula del cuadrado de una diferencia
- Suma por diferencia:
Escena que demuestra geométricamente la fórmula de la suma por diferencia
Actividades para aprender y practicar con la identidad del cuadrado de una suma.
Actividades para aprender y practicar con la identidad del cuadrado de una diferencia.
Actividades para aprender y practicar con la identidad de la suma por diferencia.
Productos notables.
Productos notables.
Productos notables. Ejemplos.
Las tres identidades notables.
La identidad notable cuadrado de una suma. Ejemplos.
La identidad notable cuadrado de una diferencia. Ejemplos.
La identidad notable suma por diferencia. Ejemplos.
- Fórmulas del cuadrado de una suma y de una diferencia.
- Ejemplos::
- a)

- b)
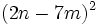
- Fórmula de la suma por diferencia.
- Ejemplos:
- a)
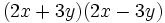
- b)
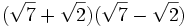
- c)
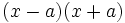
Como se desarrollan un binomio al cuadrado y una suma por diferencia.
Explicación de las igualdades o identidades notables y ejemplos resueltos.
Desarrolla:
- a)
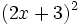
- b)
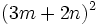
- c)
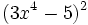
- d)
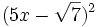
Desarrolla:
- a)
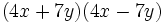
- b)
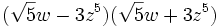
- c)

Desarrolla: 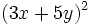
Desarrolla: 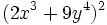
Desarrolla: 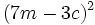
Desarrolla: 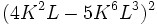
Desarrolla: 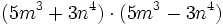
Desarrolla:
a) 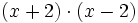
b) 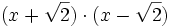
c) 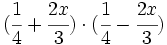
d) 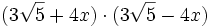
e) 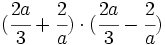
Desarrolla los siguientes productos notables:
- 2a)
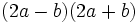
- 2b)
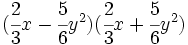
- 2c)
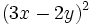
- 2d)
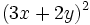
- 2e)
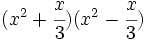
Desarrolla los siguientes productos notables:
- 4a)
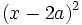
- 4b)
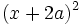
- 4c)
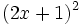
- 4d)
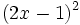
Desarrolla los siguientes productos notables:
- 5a)
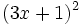
- 5b)
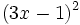
- 5c)
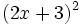
- 5d)
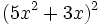
- 5e)
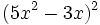
- 5f)
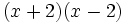
- 5g)
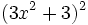
- 5h)
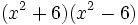
- 5i)
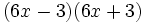
- 5j)
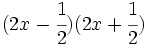
- 5k)
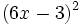
- 5l)
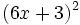
Calcula: 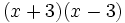
Calcula: 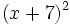
Calcula: 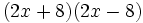
Calcula: 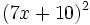
Halla el área de un cuadrado cuyo lado mide 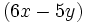 .
.
Calcula:
- a)
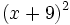
- b)
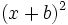
- c)
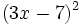
- d)
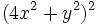
- e)
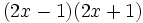
- f)
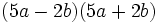
Calcula:
- a)
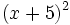
- b)
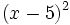
- c)
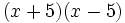
- d)
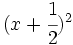
- e)
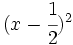
- f)
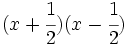
- g)
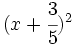
- h)
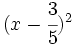
- i)
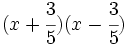
- j)
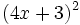
- k)
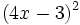
- l)
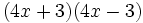
- m)
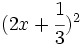
- n)
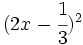
- o)
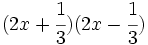
- p)
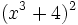
- q)
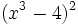
- r)
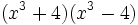
- s)
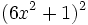
- t)
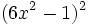
- u)
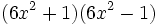
- Cubo de una suma:
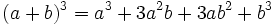
- Cubo de una diferencia:
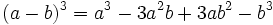
- Ejemplos.
- Suma de cubos:
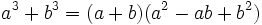
- Diferencia de cubos:
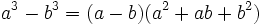
- Ejemplos.
- Cuadrado de un trinomio:
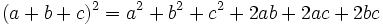
- Ejemplos.
Desarrollo del cubo de suma.
Desarrollo del cubo de diferencia.
Cuadrado de un trinomio.
Desarrolla los siguientes cuadrados de trinomios:
- 1a)
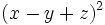
- 1b)
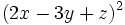
- 1c)
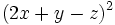
- 1d)
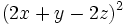
- 1e)
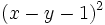
- 1f)
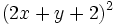
Desarrolla los siguientes cuadrados de trinomios:
- 3a)
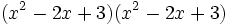
- 3b)
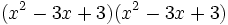
- 3c)
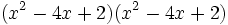
- 3d)
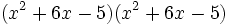
Desarrolla los siguientes cuadrados y cubos:
- 6a)
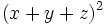
- 6b)
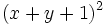
- 6c)
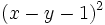
- 6d)
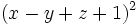
- 6e)
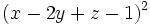
- 6f)
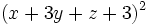
- 6g)
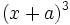
- 6h)
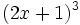
- 6i)
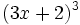
- 6j)
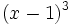
- 6k)
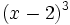
- 6l)
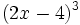
a) Sabiendo que 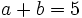 y que
y que 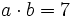 , halla
, halla 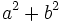 .
.
b) Sabiendo que 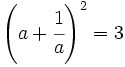 , halla
, halla 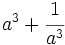 .
.
a) Efectúa: 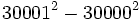 .
.
b) Halla la sexta potencia de 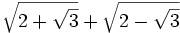 .
.
c) Sabiendo que 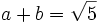 y que
y que 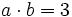 , halla
, halla 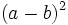 .
.
a) Reducir: 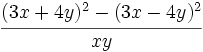 .
.
b) Efectúa: 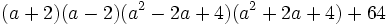 .
.
Halla: 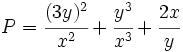 , sabiendo que
, sabiendo que 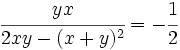 .
.
a) Sabiendo que 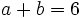 y que
y que 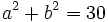 , halla
, halla 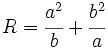 .
.
b) Si 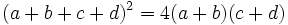 , calcula
, calcula ![\sqrt[2(a+b)]{4^{c+d}}](/wikipedia/images/math/a/3/9/a39d8769893529c6313779800e864c7c.png)
Hallar 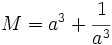 sabiendo que
sabiendo que 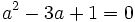 .
.
Factorización de polinomios usando productos notables
Las identidades notables son útiles para completar ciertas operaciones de forma rápida, pero una de sus aplicaciones más interesantes consiste en hacer lo contrario, deshacer cuentas. Son una potente herramienta para la descomposición y simplificación de expresiones algebraicas.
Ejemplos: Factorización de polinomios usando productos notables
Factoriza:
- a)
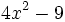
- b)
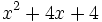
Soluciones:
a) Al tratarse de un binomio cuyos términos están restando, sólo podemos ponerlo como diferencia de cuadrados. Extrayendo las raíces cuadradas de cada término tenemos:
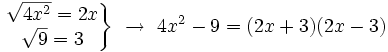
b) Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada:
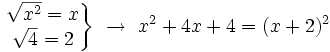
Para confirmar que esa es la factorización, comprobaremos que el doble producto del primero por el segundo es igual al otro término:
Factorización de polinomios usando productos notables. Ejemplos.
Factorización de polinomios usando productos notables. Ejemplos.
Factorización de polinomios usando el trinomio cuadrado perfecto.
Hasta el minuto 1'53": Factorización de polinomios usando diferencias de cuadrado.
Factoriza los siguientes polinomios en producto de factores usando identidades notables:
- 3a)
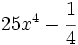
- 3b)
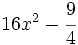
- 3c)
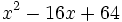
- 3d)
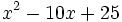
Factoriza los siguientes polinomios en producto de factores usando identidades notables:
- 3e)
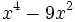
- 3f)
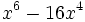
- 3g)
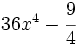
Encuentra un binomio factor común de los polinomios siguientes: 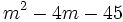 y
y 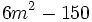
Encuentra un binomio factor común de los polinomios siguientes: 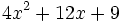 y
y 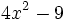
Factoriza: 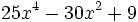
Factoriza: 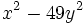
Factoriza: 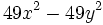
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza:
Factoriza: Factoriza: Factoriza: |
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza:
Factoriza: Factoriza: Factoriza: Factoriza: Averigua el valor de "c" y "d" de manera que Averigua el valor de "c" y "d" de manera que |
Factoriza: 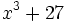
Factoriza: 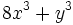
Factoriza: 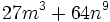
Diferencias de cuadrados:
Factorizar expresiones cuadráticas: diferencia de cuadrados
Factorizar expresiones cuadráticas: diferencia de cuadrados (Introducción)
Factorizar expresiones cuadráticas: diferencia de cuadrados
Trinomios cuadrados perfectos:
Factorizar expresiones cuadráticas: cuadrados perfectos
Factorizar expresiones cuadráticas: cuadrados perfectos
Productos notables:
Factoriza polinomios: formas de productos notables
Factoriza polinomios: formas de productos notables
Ejercicios
Ejercicios resueltos sobre identidades notables.
Ejercicios de autoevaluación sobre identidades notables.
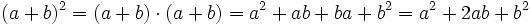
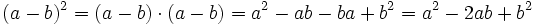
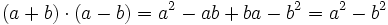
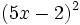
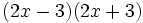
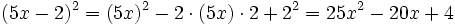
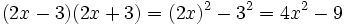
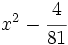
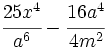
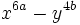
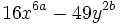
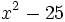

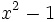
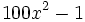
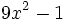
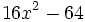

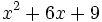

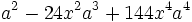
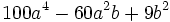
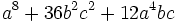
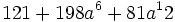
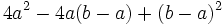
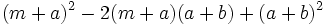
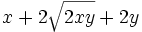
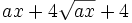
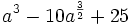
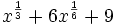
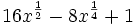
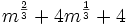
![\sqrt[3]{m^2}-6\sqrt[3]{m}+9\;](/wikipedia/images/math/a/2/a/a2a527f84cd9528ace07b344292c0c0b.png)
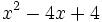
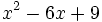
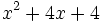
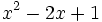
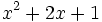

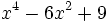
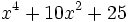
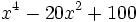
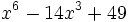
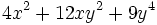
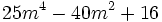
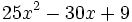
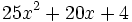
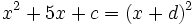 .
.