Funciones lineales: Función de proporcionalidad directa
De Wikipedia
| Revisión de 09:42 16 abr 2009 Coordinador (Discusión | contribuciones) (→Pendiente de una recta) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| - | |ir= |ampliar=[http://averroes.ced.junta-andalucia.es/iesarroyo/matematicas/materiales/3eso/solucionlibro/unidad11.pdf Ejercicios]<br>[http://mimosa.cnice.mecd.es/clobo/geoweb/geoana4.htm Ecuación pto-pendiente]<br>[http://www.ematematicas.net/ecrectaplano.php?a=5 Ecuaciones de la recta]<br> | + | |ir= |
| - | [http://www.ematematicas.net/posicionrelativa.php?a=5 Posición relativa] | + | |ampliar= |
| |repasar= | |repasar= | ||
| - | [http://descartes.cnice.mec.es/materiales_didacticos/Funcion_proporcionalidad/proporciondirecta.htm Función de Prop. Directa (en Thales)]<br>[http://descartes.cnice.mec.es/materiales_didacticos/Funcion_lineal/index.htm Función de Prop. Directa (en Descartes)]<br>[http://www.librosvivos.net/smtc/homeTC.asp?TemaClave=1067 Funciones (SM)] | + | |enlaces= |
| - | |enlaces=[http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal Función lineal]<br>[http://es.wikipedia.org/wiki/Recta Recta] | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Función lineal de proporcionalidad directa== | + | ==Función de proporcionalidad directa== |
| - | {{Caja_Amarilla|texto=Una '''función lineal de proporcionalidad directa''' es aquella cuya expresión matemática viene dada por: | + | {{Función de proporcionalidad directa}} |
| {{p}} | {{p}} | ||
| - | <center><math>y=m \cdot x</math></center> | ||
| - | {{p}} | ||
| - | donde <math>x\;\!</math> e <math>y\;\!</math> son variables y <math>m\;\!</math> una constante que se denomina '''pendiente''' o '''constante de proporcionalidad'''. Su gráfica es una recta que pasa por el origen de coordenadas.}} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Función lineal de proporcionalidad directa''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Ejemplos de funciones lineales de proporcionalidad directa. | ||
| - | |actividad={{p}} | ||
| - | * '''La función identidad.''' | ||
| - | |||
| - | La función <math>y=x\;\!</math> se denomina '''función identidad''', porque a cada número del eje de abscisas le corresponde el mismo número en el eje de ordenadas, es decir, que las dos coordenadas de cada punto son idénticas (1,1), (2,2), etc. | ||
| - | |||
| - | En la siguiente escena, mueve el punto rojo y comprueba que todos los puntos de la recta cumplen la condición <math>y=x\;\!</math>. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_1.html | ||
| - | width=560 | ||
| - | height=400 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | Como ves la representación gráfica de la función identidad es una recta, que es la bisectriz de los cuadrantes primero y tercero del sistema de referencia cartesiano. Todos los puntos de esa recta tienen sus coordenadas idénticas, para cada punto su abscisa es igual que su ordenada. | ||
| - | |||
| - | * '''Otras funciones lineales.''' | ||
| - | |||
| - | En la siguiente escena vamos a comparar las funciones <math>y=x\;\!</math> e <math>y=2x\;\!</math>. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_2.html | ||
| - | width=560 | ||
| - | height=400 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | a) Observa como la función <math>y=2x\;\!</math> asigna a cada valor <math>x\;\!</math>, su doble. Compruébalo en la gráfica. ¿Qué tienen en común ambas funciones? | ||
| - | |||
| - | Observa esta otra escena: | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_3.html | ||
| - | width=560 | ||
| - | height=400 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_3.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | b) Modifica el valor de m con los pulsadores o escribiendo el valor y pulsando "intro", para obtener las gráficas de las funciones <math>y=x\;\!</math>, <math>y=3x\;\!</math>, e <math>y=\cfrac{1}{2} \cdot x</math> | ||
| - | |||
| - | c) Dibuja las anteriores funciones en tu cuaderno a partir de sus tablas de valores. | ||
| - | |||
| - | d) ¿Qué tienen todas en común? | ||
| - | }} | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| ==Pendiente de una recta== | ==Pendiente de una recta== | ||
| ===La pendiente y el crecimiento=== | ===La pendiente y el crecimiento=== | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=La pendiente <math>m\,</math> de una recta mide la inclinación de la misma, de manera que: | + | {{La pendiente y el crecimiento}} |
| - | *Si <math>m>0\,</math>, la función es creciente. | + | |
| - | *Si <math>m<0\,</math> la función es decreciente. | + | |
| - | *Si <math>m=0\,</math> la función es constante (recta horizontal). | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''La pendiente y el crecimiento''|cuerpo= | ||
| - | |||
| - | {{ai_cuerpo | ||
| - | |enunciado=:Significado de la pendiente en relación con el crecimiento de la función lineal. | ||
| - | {{p}} | ||
| - | |actividad= | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/funcionlineal_1.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/funcionlineal_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Desliza el punto azul sobre la gráfica y observa sus coordenadas: | ||
| - | |||
| - | *¿Qué relación hay entre ellas? | ||
| - | |||
| - | Desliza ahora el punto verde para modificar el valor del parámetro m y observa los cambios. | ||
| - | |||
| - | *Describe lo que ocurre. | ||
| - | *¿Qué tienen en común y en qué se diferencian las gráficas según el valor de m? | ||
| - | *¿Cómo influye en la gráfica el signo de m? | ||
| - | *¿Que tipo de recta obtienes cuando la pendiente es 0? | ||
| - | }} | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| ===Cálculo de la pendiente=== | ===Cálculo de la pendiente=== | ||
| - | {{Teorema_sin_demo|titulo=Cálculo de la pendiente|enunciado=La pendiente de una recta se puede hallar de la siguiente manera: | + | {{Cálculo de la pendiente de y=mx}} |
| - | + | ||
| - | <center><math>m=\cfrac {variaci \acute{o} n\ de\ y}{variaci \acute{o} n\ de\ x}</math></center> | + | |
| - | + | ||
| - | para lo cual es necesario disponer de dos puntos de la recta y hallar las variaciones restando sus coordenadas '''x''' e '''y''', respectivamente. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Cálculo de la pendiente''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=:Averigua el valor de la pendiente de una recta. | ||
| - | {{p}} | ||
| - | |actividad=Consideremos la función <math>y=mx\;\!</math>, cuya pendiente es <math>m\,</math>. | ||
| - | La pendiente de una recta tiene mucha relación con las coordenadas de los puntos por donde pasa. | ||
| - | En la siguiente escena tienes que seleccionar el número que corresponde a la pendiente de la recta azul fijándote en las coordenadas del punto rojo de la recta. | ||
| - | |||
| - | Para dar valores a <math>m\;\!</math> puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro. | ||
| - | Si aciertas verás la expresión de la función con color azul, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón animar para que salga una nueva recta. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_5.html | ||
| - | width=560 | ||
| - | height=400 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/3_eso/Funcion_lineal/Funcion_lineal_5.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Ejercicios== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicio: ''Función lineal'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | '''1. '''Un grifo tiene un caudal de 5 <math>dm^3</math> por minuto. | ||
| - | :a) Haz una tabla de valores de la función tiempo-capacidad. | ||
| - | :b) Representa gráficamente la función. | ||
| - | :c) Halla la expresión algebraica de la función. | ||
| - | {{p}} | ||
| - | |sol={{p}} | ||
| - | :a) Tabla de valores:{{p}} | ||
| - | <center> | ||
| - | <table border=1> | ||
| - | <tr> | ||
| - | <td>tiempo (min)</td> | ||
| - | <td>0</td> | ||
| - | <td>1</td> | ||
| - | <td>2</td> | ||
| - | <td>3</td> | ||
| - | <td>4</td> | ||
| - | <td>5</td> | ||
| - | <td>6</td> | ||
| - | </tr> | ||
| - | <tr> | ||
| - | <td>capacidad <math>(dm^3)</math></td> | ||
| - | <td>0</td> | ||
| - | <td>5</td> | ||
| - | <td>10</td> | ||
| - | <td>15</td> | ||
| - | <td>20</td> | ||
| - | <td>25</td> | ||
| - | <td>30</td> | ||
| - | </tr> | ||
| - | </table> | ||
| - | </center> | ||
| - | {{p}} | ||
| - | |||
| - | :b) Representación gráfica: | ||
| - | {{p}} | ||
| - | [[Imagen:grifo.png|center|250px]] | ||
| - | :c) <math>y=5x</math> (<math>y</math> en <math>dm^3</math>; <math>x</math> en minutos) | ||
| - | }} | ||
| - | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Función de proporcionalidad directa
Una función de proporcionalidad directa es aquella cuya expresión analítica puede expresarse como:
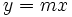 |
 es la variable independiente.
es la variable independiente.
 es la variable dependiente.
es la variable dependiente.
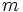 una constante que se denomina constante de proporcionalidad o pendiente.
una constante que se denomina constante de proporcionalidad o pendiente.
Representación gráfica
- La gráfica de una función de proporcionalidad directa es una recta que pasa por el origen de coordenadas.
- En consecuencia, para representarla sólo necesitamos un punto y el origen, los cuales uniremos mediante una línea recta. Para obtener dicho punto usaremos la ecuación.
Ejemplo: Función de proporcionalidad directa
Un grifo, con un caudal de 5 dm3 por minuto, vierte agua en una piscina.
- a) Haz una tabla de valores de la función que relaciona el tiempo con el volumen que se llena.
- b) Halla la expresión analítica de la función.
- c) Representa gráficamente la función.
Solución:
- La variable independiente es el tiempo transcurrido y la dependiente el volumen que ocupa el agua vertida en ese tiempo.
- a) Tabla de valores:
| tiempo (min) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Volumen (dm3) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
- b) Expresión analítica:
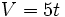 (V en dm3; t en minutos)
(V en dm3; t en minutos)
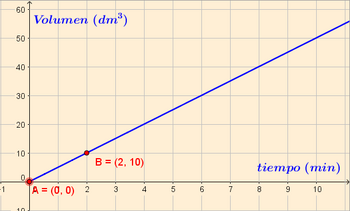
- c) Representación gráfica: Como se trata de una función de proporcionalidad directa, su gráfica es una recta que pasa por el origen. Por tanto, solo tendremos que representar un punto y el origen, y unirlos mediante una línea recta.
- Sólo se representan los valores
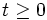 , ya que el tiempo empieza a contar a partir de cero.
, ya que el tiempo empieza a contar a partir de cero.
Función de proporcionalidad directa. Expresión analítica y gráfica.
Variable independiente y dependiente en una función de proporcionalidad directa dada por una ecuación y su correspondiente tabla.
Ejemplo de representación gráfica de una función de proporcionalidad directa dada por una ecuación y su correspondiente tabla.
Ejemplo sobre la obtención de la ecuación de una función de proporcionalidad directa a partir de su gráfica y de su correspondiente tabla.
En esta escena podrás ver e interactuar con las gráficas de funciones de proporcionalidad directa y estudiar sus propiedades.
Definición de función de proporcionalidad directa. Ejemplos.
Actividades en las que aprenderás a representar funciones de proporcionalidad directa y a identificar su ecuación a partir de su gráfica.
Función identidad
Si 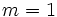 , la función que se obtiene,
, la función que se obtiene, 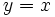 , recibe el nombre de función identidad y es la bisectriz del primer y tercer cuadrante.
, recibe el nombre de función identidad y es la bisectriz del primer y tercer cuadrante.
Pendiente de una recta
La pendiente y el crecimiento
Propiedades
La pendiente,  , describe el crecimiento de la función
, describe el crecimiento de la función 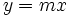 :
:
- Si
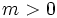 , la función es creciente.
, la función es creciente.
- Si
 la función es decreciente.
la función es decreciente.
- Si
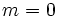 la función es constante (recta horizontal).
la función es constante (recta horizontal).
Además, cuanto mayor es su pendiente (en valor absoluto), más inclinada es su gráfica.
En esta escena podrás ver como afecta el signo de la pendiente al crecimiento de la función.
Cálculo de la pendiente
La pendiente de una función de proporcionalidad directa se puede hallar de la siguiente manera:
Proposición
Consideremos una función de proporcionalidad directa 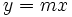 y un punto
y un punto 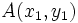 de la recta que la representa, distinto del origen.
de la recta que la representa, distinto del origen.
La pendiente se puede calcular de la siguiente manera:
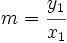
En consecuencia, conocido un punto distinto del origen, es posible determinar la ecuación de la función de proporcionaliedad directa cuya gráfica pasa por ese punto.
Es inmediato, pués si 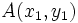 es un punto de la recta
es un punto de la recta 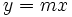 , cumplirá su ecuación:
, cumplirá su ecuación:
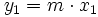
Despejando, tenemos:
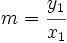
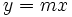 .
.En esta escena podrás ver como se calcula la pendiente de una función de proporcionalidad directa y como se obtiene su ecuación.
Consideremos la función 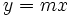 , cuya pendiente es
, cuya pendiente es  .
.
La pendiente de una recta tiene mucha relación con las coordenadas de los puntos por donde pasa.
En la siguiente escena tienes que seleccionar el número que corresponde a la pendiente de la recta azul fijándote en las coordenadas del punto rojo de la recta.
Para dar valores a 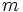 puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro.
Si aciertas verás la expresión de la función con color azul, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón "animar" para que salga una nueva recta.
puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro.
Si aciertas verás la expresión de la función con color azul, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón "animar" para que salga una nueva recta.