Posición relativa de dos rectas
De Wikipedia
| Revisión de 16:42 11 sep 2007 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| - | |ir= |ampliar=[http://averroes.ced.junta-andalucia.es/iesarroyo/matematicas/materiales/3eso/solucionlibro/unidad11.pdf Ejercicios]<br>[http://mimosa.cnice.mecd.es/clobo/geoweb/geoana4.htm Ecuación pto-pendiente]<br>[http://www.ematematicas.net/ecrectaplano.php?a=5 Ecuaciones de la recta]<br> | + | |ir= |
| - | [http://www.ematematicas.net/posicionrelativa.php?a=5 Posición relativa] | + | |ampliar= |
| |repasar= | |repasar= | ||
| - | [http://descartes.cnice.mecd.es/1y2_eso/Funciones_funcion_de_proporcionalidad/index.htm Proporcionalidad directa] | + | |enlaces= |
| - | |enlaces=[http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal Función lineal]<br>[http://es.wikipedia.org/wiki/Recta Recta] | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| ==Posición relativa de dos rectas== | ==Posición relativa de dos rectas== | ||
| - | Dos rectas del plano pueden ocupar una de las tres posiciones siguientes: | + | {{Posición relativa de dos rectas}} |
| - | {{Caja_Amarilla|texto= | + | |
| - | * '''Secantes:''' Se cortan en un punto. | + | |
| - | * '''Paralelas:''' No se cortan. | + | |
| - | * '''Coincidentes:''' Tienen infinitos puntos en común, son la misma recta. | + | |
| - | }}{{p}} | + | |
| - | Para determinar la posición relativa de dos rectas podemos recurrir a la resolución del sistema formado por las dos ecuaciones. | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | Dependiendo del número de soluciones del sistema tendremos: | + | |
| - | * '''1 solución:''' Las rectas son secantes. | + | |
| - | * '''0 soluciones:''' Las rectas son paralelas. | + | |
| - | * '''Infinitas soluciones:''' Las rectas son coincidentes. | + | |
| - | }}{{p}} | + | |
| - | También se puede recurrir a comparar las pendientes y las ordenadas en el origen de cada recta: | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | * '''Distintas pendientes:''' Las rectas son secantes. | + | |
| - | * '''Igual pendiente y distinta ordenada en el origen:''' Las rectas son paralelas. | + | |
| - | * '''Igual pendiente e igual ordenada en el origen:''' Las rectas son coincidentes. | + | |
| - | }} | + | |
| - | ==Ejercicios== | + | |
| - | {{ejercicio | + | |
| - | |titulo=Problema: ''Posición relativa de dos rectas'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
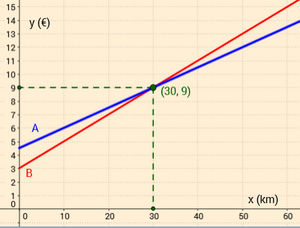
| - | '''1. '''Una empresa de transporte A tiene las siguientes tarífas: 0,20 € por kilómetro de recorrido y 3 € por paquete. Las tarifas de otra empresa B son: 0,15 € por kilómetro y 4,50 € por paquete. | + | |
| - | :a) Representa gráficamente estas tarifas. | + | |
| - | :b) Explica que empresa es más conveniente contratar para llevar un paquete. | + | |
| {{p}} | {{p}} | ||
| - | |sol= | + | ==Perpendicularidad entre rectas== |
| + | {{Perpendicularidad entre rectas}} | ||
| {{p}} | {{p}} | ||
| - | :a) Representación gráfica: | + | ==Ejercicios== |
| - | {{p}}[[Imagen:tarifastransporte.png|center|250px]]{{p}} | + | {{ejercicio: Estudio conjunto de dos funciones lineales}} |
| - | :b) A partir de 30 km interesa la empresa B. Para menos interesa la A. | + | [[Categoría: Matemáticas]][[Categoría: Funciones]] |
| - | }} | + | |
| - | }} | + | |
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Posición relativa de dos rectas
Dos rectas del plano pueden ocupar una de las tres posiciones siguientes:
- Secantes: Se cortan en un punto.
- Paralelas: No se cortan.
- Coincidentes: Tienen infinitos puntos en común, son la misma recta.
Procedimiento
Para determinar la posición relativa de dos rectas podemos recurrir a:
1. Resolver el sistema formado por las dos ecuaciones y dependiendo del número de soluciones del sistema tendremos:
- 1 solución: Las rectas son secantes.
- 0 soluciones: Las rectas son paralelas.
- Infinitas soluciones: Las rectas son coincidentes.
2. Comparar las pendientes y las ordenadas en el origen de cada recta:
- Distintas pendientes: Las rectas son secantes.
- Igual pendiente y distinta ordenada en el origen: Las rectas son paralelas.
- Igual pendiente e igual ordenada en el origen: Las rectas son coincidentes.
Paralelismo entre rectas del plano Descripción: En esta escena podrás ver e interactuar con dos rectas paralelas y ver que las caracteriza.
Actividades en las que aprenderás a averiguar la posición relativa de dos rectas dadas en forma explícita.
Actividades en las que aprenderás a averiguar la posición relativa de dos rectas dadas en forma general.
Perpendicularidad entre rectas
Propiedad
Dos rectas, con pendientes m y m', son perpendiculares si y sólo si sus pendientes son inversas y opuestas simultaneamente:
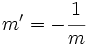
O equivalentemente, cuando el producto de ambas pendientes es igual a -1:
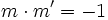
Perpendicularidad entre rectas Descripción: En esta escena podrás ver e interactuar con dos rectas perpendiculares y ver que las caracteriza.
Ejercicios
Problemas resueltos en los que intervienen dos funciones lineales que hay que relacionar.
 Problema: Estudio conjunto de dos funciones lineales 1. Una empresa de transporte A tiene las siguientes tarífas: 0,20 € por kilómetro de recorrido y 3 € por paquete. Las tarifas de otra empresa B son: 0,15 € por kilómetro y 4,50 € por paquete.
Solución: a) Representación gráfica:
 |
