Gráficos estadísticos
De Wikipedia
| Revisión de 21:21 19 jun 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar: | + | __TOC__ |
| - | {{AI | + | {{Gráficos estadísticos}} |
| - | Diagrama de barras o rectángulos. Consiste en dos ejes perpendiculares y una barra o rectángulo para cada valor de la variable. Normalmente, se suele colocar en el eje horizontal los valores de la variable (aunque también se puede hacer en el vertical). El otro eje se gradúa según los valores de las frecuencias. La representación gráfica consiste en dibujar una barra o un rectángulo para cada uno de los valores de la variable de altura igual a su frecuencia. | + | |
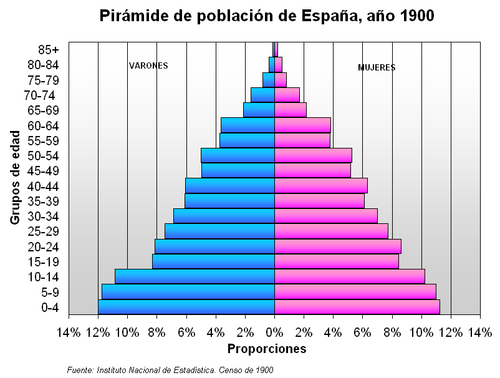
| - | Histograma de frecuencias. Es un caso particular del diagrama anterior en el caso de variables continuas. Si los intervalos son correlativos, los rectángulos aparecen pegados en la representación gráfica. En caso de que la amplitud de los intervalos no se igual para todos, hay que hacer coincidir el área del rectángulo con la frecuencia del intervalo. Un ejemplo muy utilizado de histograma es una pirámide de población. | + | [[Categoría: Matemáticas]][[Categoría: Estadística]] |
| - | + | ||
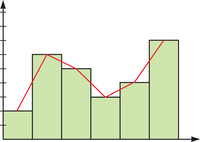
| - | Polígono de frecuencias. Representamos dos ejes perpendiculares y representamos en el horizontal los valores de la variable y en el vertical las frecuencias. Representamos los puntos que tiene por primera coordenada el valor de la variable y por segunda el valor de la frecuencia. Uniendo todos los puntos obtenemos una línea poligonal que es la representación que buscamos. | + | |
| - | + | ||
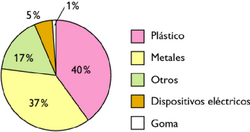
| - | Diagrama de sectores. Consiste en dividir un círculo en tantos sectores como valores de la variable. La amplitud de cada sector debe ser proporcional a la frecuencia del valor correspondiente. | + | |
Revisión actual
Tabla de contenidos[esconder] |
Gráficos estadísticos
Ya sabemos construir la tabla de frecuencias para una distribución estadística. Ahora vamos a representar mediante distintos gráficos la información recopilada.
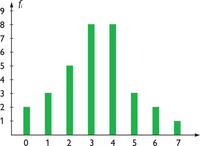
Diagrama de barras
Un diagrama de barras consiste en dos ejes perpendiculares y una barra o rectángulo para cada valor de la variable. Se utiliza para datos agrupados puntualmente para variables tanto cualitativas, como cuantitativas.
|  |
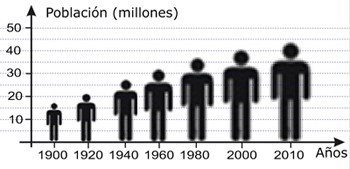
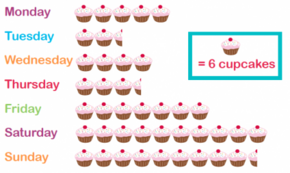
Pictogramas
Si en un diagrama de barras sustituimos las barras por un dibujo alusivo al carácter que se está estudiando, tenemos un pictograma.
Un pictograma es un gráfico con dibujos alusivos al carácter que se está estudiando y cuyo tamaño es proporcional a la frecuencia que representan. En vez de utilizar dibujos de distinto tamaño, también puede repetirse un mismo dibujo las veces necesarias para representar la frecuencia deseada. En este caso, a cada dibujo se le asigna un mismo valor, y la suma de los valores de los dibujos de cada carácter deberá ser igual a su frecuencia.
 Número de habitantes por año de una población
|  Número de pasteles vendidos cada día de la semanade http://schoolrun.com
|
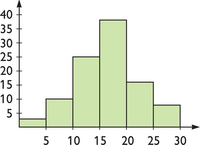
Histograma
Es un caso particular del diagrama anterior para el caso de variables continuas o que tomen muchos valores y sea necesario agruparlos por intervalos. En caso de que la amplitud de los intervalos no se igual para todos, hay que hacer coincidir el área del rectángulo con la frecuencia del intervalo. |  |
Polígono de frecuencias
|  |
Diagrama de sectores
Un diagrama de sectores consiste en dividir un círculo en tantos sectores como valores tome la variable, siendo la amplitud de cada sector proporcional a la frecuencia del valor correspondiente. Sirve para variables cualitativas y cuantitativas. |  |
