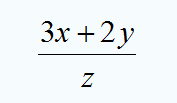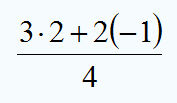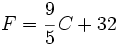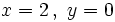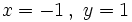Plantilla:Valor numérico de una expresión algebraica
De Wikipedia
| Revisión de 16:33 24 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| + | {{tabla75|celda2=[[Imagen:valor_num.gif|thumb|Valor numérico de (3x+2y)/z para x=2, y=-1 y z=4.]] | ||
| + | |celda1=El lenguaje algebraico sirve para pasar de casos particulares a casos generales, sin embargo, en muchas ocasiones haremos el proceso inverso, pasaremos de una expresión general a un valor concreto. | ||
| + | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Si en una expresión algebraica se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el '''valor númerico''' de la expresión algebraica para los valores de las letras dados. | + | Si en una expresión algebraica se sustituyen las letras (variables) por números y se realizan las operaciones correspondientes, se obtiene un número al que llamaremos el '''valor númerico''' de la expresión algebraica para los valores de las letras asignados. |
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Valor numérico de una expresión algebraica'' | {{Ejemplo|titulo=Ejemplo: ''Valor numérico de una expresión algebraica'' | ||
| - | |enunciado=Halla el valor numérico de los polinomios: | + | |enunciado=Halla el valor numérico: |
| {{p}} | {{p}} | ||
| :a) {{sube|porcentaje=20%|contenido=<math>3x^5+2x\;\!</math>}} para {{sube|porcentaje=20%|contenido=<math>x=2\;\!</math>}} | :a) {{sube|porcentaje=20%|contenido=<math>3x^5+2x\;\!</math>}} para {{sube|porcentaje=20%|contenido=<math>x=2\;\!</math>}} | ||
| Línea 10: | Línea 14: | ||
| :b) {{sube|porcentaje=20%|contenido=<math>2xy-3y^2+5\;</math>}} para {{sube|porcentaje=20%|contenido=<math>x=1\;</math>}} e <math>y=2\;</math>. | :b) {{sube|porcentaje=20%|contenido=<math>2xy-3y^2+5\;</math>}} para {{sube|porcentaje=20%|contenido=<math>x=1\;</math>}} e <math>y=2\;</math>. | ||
| |sol= | |sol= | ||
| - | a) El valor numérico del polinomio es: {{sube|porcentaje=20%|contenido=<math>3 \cdot 2^5+2 \cdot 2=100</math>}} | + | a) El valor numérico es: {{sube|porcentaje=20%|contenido=<math>3 \cdot 2^5+2 \cdot 2=100</math>}} |
| - | b) El valor numérico del polinomio es: {{sube|porcentaje=20%|contenido=<math>2 \cdot 1 \cdot 2 -3 \cdot 2^2 + 5=-3</math>}} | + | b) El valor numérico es: {{sube|porcentaje=20%|contenido=<math>2 \cdot 1 \cdot 2 -3 \cdot 2^2 + 5=-3</math>}} |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_enlace | + | {{Videotutoriales|titulo=Valor numérico de una expresión algebraica|enunciado= |
| - | |titulo1=Actividad Interactiva: ''Valor numérico de una expresión algebraica'' | + | {{Video_enlace_clasematicas |
| - | |descripcion= | + | |titulo1=Tutorial 1 |
| - | '''1.''' Calcula el valor numérico del polinomio {{sube|porcentaje=20%|contenido=<math>a^2-2ax+4\;\!</math>}} en los casos:{{p}} | + | |duracion=19'18" |
| - | {{b4}}a) <math>a=2 \, , \ x=3\;\!</math> | + | |sinopsis=Tutorial en el que se explica y trabaja el cálculo del valor numérico de expresiones algebraicas de una o más variables, así como las tablas de valores. |
| + | |url1=https://www.youtube.com/watch?v=Uc711Wf1rRg&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM&index=1 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=4'02" | ||
| + | |sinopsis=En este video vamos a ver lo que es el valor numérico de una expresión algebraica y cómo se calcula.|url1=https://www.youtube.com/watch?v=WvVvLrTJVjk&index=3&list=PLw7Z_p6_h3ozJ3jNAIYHmEpSM6m24aPG2 | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=1'52" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>4x+2\;</math> para <math>x=\cfrac{1}{3}\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=qxViTt1N3QY | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=1'15" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>\cfrac{x}{2}+4\;</math> para <math>x=-2\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=E0nu4mvTYHI | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=1'15" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>3x+6\;</math> para <math>x=-1\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=Us7L-BoeM2Q | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=1'32" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>\cfrac{9-2n}{2}\;</math> para <math>n=3\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=kc55U-KQKBI | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=2'03" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>\cfrac{2n^2}{6n}\;</math> para <math>n=5\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=J7XlO2uSPbw | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=1'22" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>23n+8n\;</math> para <math>n=3\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=OutZTbq-Hqg | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=1'11" | ||
| + | |sinopsis=Calcula el valor numérico de la expresión algebraica <math>-5x+1\;</math> para <math>x=-7\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=Y76gy8RLWEU | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=8'11" | ||
| + | |sinopsis=Calcula el valor numérico de las siguientes expresiones algebraicas para los valores indicados de las variables: | ||
| - | {{b4}}b) <math>a=-2 \, , \ x=1\;\!</math> | + | :51) <math>3x-5 \ para \ x=2\;</math> |
| + | :52) <math>5x-8 \ para \ x=-1\;</math> | ||
| + | :53) <math>4x+3 \ para \ x=6\;</math> | ||
| + | :54) <math>x^2+1 \ para \ x=-1\;</math> | ||
| + | :55) <math>x^3-1 \ para \ x=1\;</math> | ||
| + | :56) <math>5x-2 \ para \ x=-4\;</math> | ||
| + | :57) <math>\cfrac{2x+3}{x} \ para \ x=2\;</math> | ||
| + | :58) <math>\cfrac{x^2-1}{x+1} \ para \ x=-2\;</math> | ||
| + | :59) <math>\cfrac{2x+3}{x-2} \ para \ x=3\;</math> | ||
| - | '''2.''' Encuentra algún valor de <math>x\;</math> y <math>a\;</math> que hagan que el valor numérico valga cero. | + | |url1=https://www.youtube.com/watch?v=wh-LXfOWHoU&list=PLw7Z_p6_h3ozJ3jNAIYHmEpSM6m24aPG2&index=8 |
| - | ---- | + | }} |
| - | Haz uso de la siguiente escena para comprobar los resultados: | + | {{Video_enlace_khan |
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=2'03" | ||
| + | |sinopsis=Un hospital local está realizando una rifa para recolectar fondos. El coste individual para participar en la rifa está dado por la expresión <math>5t + 3\;</math>, donde <math>t\;</math> representa el número de boletos que la persona adquiere. Evalúa la expresión para <math>t = 1\;</math>, <math>t = 8\;</math> y <math>t = 10\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=o4qqOPsKq9Y | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=2'46" | ||
| + | |sinopsis= | ||
| + | :a) Evalúa la expresión <math>a + b\;</math> para <math>a = 7\;</math> y <math>b = 2\;</math>. | ||
| + | :b) Evalúa la expresión <math>xy-y+3x\;</math> para <math>x = 3\;</math> e <math>y = 2\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=EoABWierj_w | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=4'05" | ||
| + | |sinopsis= | ||
| + | :a) Evalúa la expresión <math>7j + 5 - 8k\;</math> para <math>j = 0.5\;</math> y <math>k = 0.25\;</math>. | ||
| + | :b) Evalúa la expresión <math>0.1m + 8 - 12n\;</math> para <math>m = 30\;</math> y <math>n = \cfrac{1}{4}\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=pTmo-Dj0-es | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 12 | ||
| + | |duracion=6'36" | ||
| + | |sinopsis= | ||
| + | :a) ¿Qué le ocurre a la expresión <math>100-x\;</math> cuando la variable <math>x\;</math> va disminuyendo? | ||
| + | :b) ¿Qué le ocurre a la expresión <math>\cfrac{5}{x}+5\;</math> cuando la variable <math>x\;</math> va disminuyendo, pero manteniéndose positiva? | ||
| + | |url1=https://www.youtube.com/watch?v=l8GtXUUiBOM | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 13 | ||
| + | |duracion=1'17" | ||
| + | |sinopsis=Expresa 25º Celsius (C) como una temperatura en grados Fahrenheit (F), usando la fórmula: | ||
| + | |||
| + | :<math>F=\cfrac{9}{5}\,C+32\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=lUQQolpDzKk | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 14 | ||
| + | |duracion=3'26" | ||
| + | |sinopsis=El área de la superficie de un cubo es igual a la suma de las áreas de sus 6 caras. En consecuencia, vendrá dada por la fórmula <math>A=6x^2\;</math>, siendo <math>x\;</math> el valor de la arista del cubo. | ||
| + | |||
| + | Julia tiene dos recipientes de forma cúbica que quiere pintar. Uno tiene arista 2 y otro 1.5. Calcula el área total que quiere pintar. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=3D02VIEjM2c | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 15 | ||
| + | |duracion=2'44" | ||
| + | |sinopsis=Evalúa la expresión <math>5y^4-y^2\;</math> cuando <math>y=3\;</math>. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=CdcvOYBzXnk | ||
| + | }} | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | <center><iframe> | + | {{Actividades|titulo=Valor numérico de una expresión algebraica|enunciado= |
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Polinomios/monomios_1.html | + | {{AI_cidead |
| - | width=440 | + | |titulo1=Actividad 1a |
| - | height=250 | + | |descripcion=Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica. |
| - | name=myframe | + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_1c.htm |
| - | </iframe></center> | + | }} |
| - | |url1=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Polinomios/monomios_1.html | + | {{AI_cidead |
| + | |titulo1=Actividad 1b | ||
| + | |descripcion=Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_1c.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2a | ||
| + | |descripcion=Evaluar expresiones con una sola variable. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/a/evaluating-expressions-with-one-variable | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2b | ||
| + | |descripcion=Evaluar expresiones con dos variables. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/a/evaluating-expressions-with-two-variables | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2c | ||
| + | |descripcion=Evaluar expresiones con dos variables: fracciones y decimales. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/a/evaluating-expressions-with-two-variables-with-fractions-and-decimals | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2d | ||
| + | |descripcion=Intuición sobre el valor de una expresión. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-expression-value-intuitionss/a/thinking-about-changing-values-of-variables-and-expressions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2e | ||
| + | |descripcion=Intuición sobre el valor de una expresión. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-expression-value-intuitionss/a/thinking-about-changing-values-of-variables-and-expressions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2f | ||
| + | |descripcion=Evaluar expresiones con variables: problemas verbales. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-evaluating-expressions-word-problems/a/evaluating-expressions-with-variables-in-word-problems | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1a | ||
| + | |descripcion=Evaluar expresiones con una sola variable. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/e/evaluating_expressions_1 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1b | ||
| + | |descripcion=Evaluar expresiones con múltiples variables. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/e/evaluating_expressions_2 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1c | ||
| + | |descripcion=Evaluar expresiones con múltiples variables: fracciones y decimales. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-substitution/e/evaluating-expressions-in-two-variables-2 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1d | ||
| + | |descripcion=Intuición sobre el valor de una expresión. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-expression-value-intuitionss/e/expression-value-intuition | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1e | ||
| + | |descripcion=Evaluar expresiones con variables: problemas verbales. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-evaluating-expressions-word-problems/e/evaluating-expressions-3 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1f | ||
| + | |descripcion=Evaluar expresiones con potencias. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-exponents-radicals/pre-algebra-exponents/e/exponents-in-expressions | ||
| + | }} | ||
| + | {{AI_melide | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | |descripcion=Autoevaluación sobre el valor numérico de una expresión algebraica. | ||
| + | |||
| + | |url1=http://maralboran.org/web_ma/Melide/Expresiones%20algebraicas/Valor_%20numerico.html}} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
| El lenguaje algebraico sirve para pasar de casos particulares a casos generales, sin embargo, en muchas ocasiones haremos el proceso inverso, pasaremos de una expresión general a un valor concreto.
Si en una expresión algebraica se sustituyen las letras (variables) por números y se realizan las operaciones correspondientes, se obtiene un número al que llamaremos el valor númerico de la expresión algebraica para los valores de las letras asignados. |
Ejemplo: Valor numérico de una expresión algebraica
Halla el valor numérico:
- a)
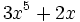 para
para 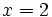
- b)
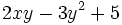 para
para 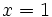 e
e 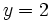 .
.
a) El valor numérico es: 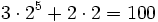
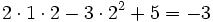
Tutorial en el que se explica y trabaja el cálculo del valor numérico de expresiones algebraicas de una o más variables, así como las tablas de valores.
En este video vamos a ver lo que es el valor numérico de una expresión algebraica y cómo se calcula.
Calcula el valor numérico de la expresión algebraica 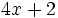 para
para 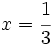 .
.
Calcula el valor numérico de la expresión algebraica 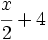 para
para 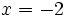 .
.
Calcula el valor numérico de la expresión algebraica 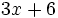 para
para 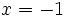 .
.
Calcula el valor numérico de la expresión algebraica 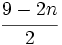 para
para 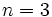 .
.
Calcula el valor numérico de la expresión algebraica 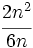 para
para 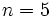 .
.
Calcula el valor numérico de la expresión algebraica 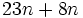 para
para 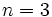 .
.
Calcula el valor numérico de la expresión algebraica 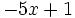 para
para 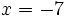 .
.
Calcula el valor numérico de las siguientes expresiones algebraicas para los valores indicados de las variables:
- 51)
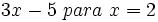
- 52)
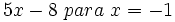
- 53)
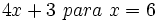
- 54)
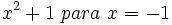
- 55)
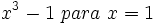
- 56)
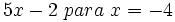
- 57)
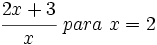
- 58)
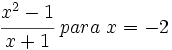
- 59)
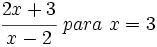
Un hospital local está realizando una rifa para recolectar fondos. El coste individual para participar en la rifa está dado por la expresión 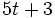 , donde
, donde 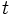 representa el número de boletos que la persona adquiere. Evalúa la expresión para
representa el número de boletos que la persona adquiere. Evalúa la expresión para 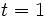 ,
, 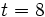 y
y 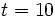 .
.
- a) Evalúa la expresión
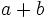 para
para 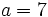 y
y 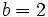 .
.
- b) Evalúa la expresión
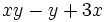 para
para  e
e 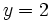 .
.
- a) Evalúa la expresión
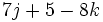 para
para 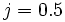 y
y 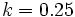 .
.
- b) Evalúa la expresión
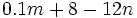 para
para 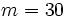 y
y  .
.
- a) ¿Qué le ocurre a la expresión
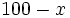 cuando la variable
cuando la variable  va disminuyendo?
va disminuyendo?
- b) ¿Qué le ocurre a la expresión
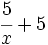 cuando la variable
cuando la variable  va disminuyendo, pero manteniéndose positiva?
va disminuyendo, pero manteniéndose positiva?
Expresa 25º Celsius (C) como una temperatura en grados Fahrenheit (F), usando la fórmula:
El área de la superficie de un cubo es igual a la suma de las áreas de sus 6 caras. En consecuencia, vendrá dada por la fórmula 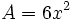 , siendo
, siendo  el valor de la arista del cubo.
el valor de la arista del cubo.
Julia tiene dos recipientes de forma cúbica que quiere pintar. Uno tiene arista 2 y otro 1.5. Calcula el área total que quiere pintar.
Evalúa la expresión 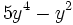 cuando
cuando 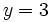 .
.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Evaluar expresiones con una sola variable.
Evaluar expresiones con dos variables.
Evaluar expresiones con dos variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con una sola variable.
Evaluar expresiones con múltiples variables.
Evaluar expresiones con múltiples variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con potencias.
Autoevaluación sobre el valor numérico de una expresión algebraica.