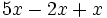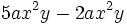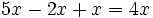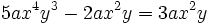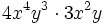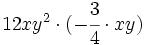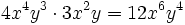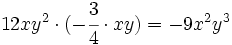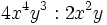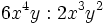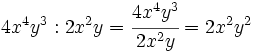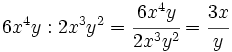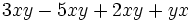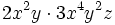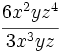Plantilla:Operaciones con monomios
De Wikipedia
| Revisión de 07:09 17 oct 2017 Coordinador (Discusión | contribuciones) (→Suma y resta de monomios) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios) |
||
| Línea 3: | Línea 3: | ||
| {{Suma y resta de monomios}} | {{Suma y resta de monomios}} | ||
| {{p}} | {{p}} | ||
| - | ====Opuesto de un monomio==== | + | |
| - | {{Opuesto de un monomio}} | + | |
| - | {{p}} | + | |
| ===Multiplicación y división de monomios=== | ===Multiplicación y división de monomios=== | ||
| Línea 24: | Línea 22: | ||
| {{Ejercicios: Operaciones con monomios}} | {{Ejercicios: Operaciones con monomios}} | ||
| {{wolfram: operaciones monomios}} | {{wolfram: operaciones monomios}} | ||
| + | {{p}} | ||
| + | |||
| + | ==Ejercicios== | ||
| + | {{Actividades: Monomios y operaciones}} | ||
| + | {{p}} | ||
| + | ==Apéndice== | ||
| + | {{Introducción al análisis dimensional}} | ||
Revisión actual
Tabla de contenidos |
Suma y resta de monomios
Procedimiento
Para sumar o restar dos monomios tienen que ser semejantes. La suma o resta es otro monomio semejante a ellos que tiene por coeficiente la suma o diferencia, según el caso, de los coeficientes.
Suma y resta de monomios. Monomios opuestos.
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Aprende a sumar y restar monomios
Agrupa (reduce) términos semejantes:
a) 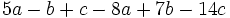
b) 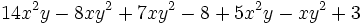
Reduce:
a) 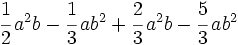
b) 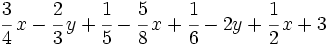
Realiza las siguientes sumas y restas de monomios:
- 22)
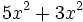 ; 23)
; 23) 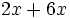 ; 24)
; 24) 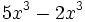
- 25)
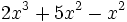 ; 26)
; 26) 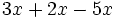 ; 27)
; 27) 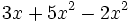
- 28)
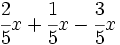 ; 29)
; 29)  ; 30)
; 30) 
- 31)
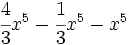 ; 32)
; 32) 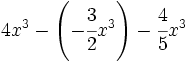
Actividades en la que aprenderás y practicarás a sumar y restar monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Actividades para practicar la suma y resta de monomios.
Multiplicación y división de monomios
Cómo se multiplican y dividen monomios. Ejemplos.
Multiplicación y división de monomios. Potencias de monomios.
Producto de monomios
Procedimiento
Para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican.
Recordemos que: para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes.
Multiplicación de monomios. Ejemplos.
Haz las siguientes multiplicaciones de monomios:
- a)
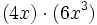
- b)
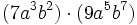
- c)
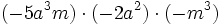
Haz las siguientes multiplicaciones de monomios:
- a)
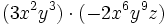
- b)
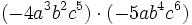
- c)
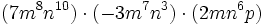
- d)
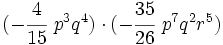
Haz las siguientes multiplicaciones de monomios:
- a)
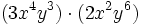
- b)
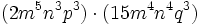
- c)
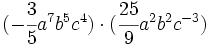
Multiplica los siguientes monomios:
- 37)
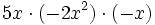 ; 38)
; 38) 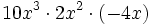 ; 39)
; 39) 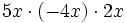
- 40)
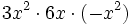 ; 41)
; 41) 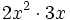 ; 42)
; 42) 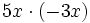
- 43)
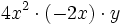 ; 44)
; 44) 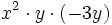
Multiplica los siguientes monomios:
- 45)
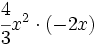 ; 46)
; 46) 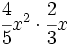 ; 47)
; 47) 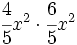
- 48)
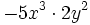 ; 49)
; 49) 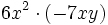 ; 50)
; 50) 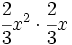
- 51)
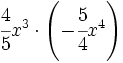 ; 52)
; 52) 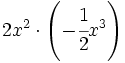 ; 53)
; 53) 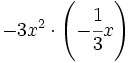
Expresa en forma de un monomio el área de un rectángulo que mide 4y de largo y 2y de ancho.
Expresa en forma de un monomio el área de un rectángulo que mide 4xy de largo y 2y de ancho.
Averigua el valor de "a" y "b" sabiendo que 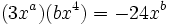 .
.
Actividades en la que aprenderás y practicarás a multiplicar monomios.
Actividades para practicar la multiplicación de monomios.
Multiplicación de monomios.
Multiplicación de monomios.
División de monomios
Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Aprende a dividir monomios
Divide:
- a)
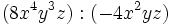
- b)
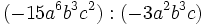
- c)
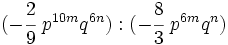
Divide los siguientes monomios:
- 54)
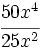 ; 55)
; 55) 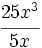 ; 56)
; 56) 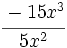 ; 57)
; 57) 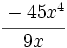
- 58)
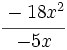 ; 59)
; 59) 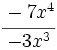 ; 60)
; 60) 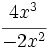 ; 61)
; 61) 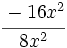
- 62)
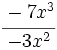 ; 63)
; 63) 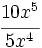 ; 64)
; 64) 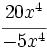 ; 65)
; 65) 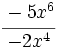
Potencias de monomios
Para calcular la potencia de un monomio aplicaremos la propiedad de la potencia de un producto (la potencia de un producto de factores es igual al producto de las potencias de cada factor) y la propiedad de la potencia de otra potencia (la potencia de otra potencia es igual a otra potencia cuyo exponente es el producto de los exponentes).
Calcula las siguientes potencias de monomios:
- 66)
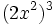 ; 67)
; 67) 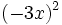 ; 68)
; 68) 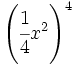 ; 69)
; 69) 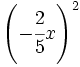
- 70)
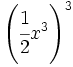 ; 71)
; 71) 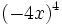 ; 72)
; 72) 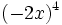 ; 73)
; 73) 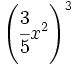
- 74)
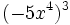 ; 75)
; 75) 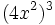 ; 76)
; 76) 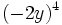 ; 77)
; 77) 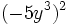
- 78)
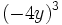 ; 79)
; 79) 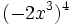 ; 80)
; 80) 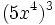
Actividades
Operaciones con monomios:
- a)
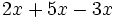
- b)
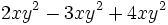
- c)
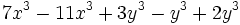
- d)
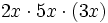
- e)
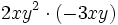
- f)
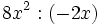
- g)
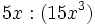
Ejercicios de autoevaluación sobre operaciones con monomios.
Ejercicios
Ejercicios resueltos sobre monomios.
Ejercicios de autoevaluación sobre monomios.
Apéndice
Introducción al análisis dimensional.
Otro ejemplo de análisis dimensional.
Elige la respuesta adecuada (ver video).
Elige la respuesta adecuada (ver video).
Supervivencia de una ardilla.
Coste de la gasolina para un viaje.
Convertir unidades de longitud.
Convertir unidades: dosis medicinal.
Autoevaluación sobre análisis dimensional.
Problemas de tasas.
Problemas de varais unidades.