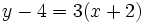Plantilla:Ecuación punto-pendiente de una recta
De Wikipedia
| Revisión de 14:09 9 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | |||
| Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado: | Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado: | ||
| {{Teorema | {{Teorema | ||
| Línea 29: | Línea 28: | ||
| sustituimos <math>m=3\;</math>, <math>x_o=-2\;</math>, <math>y_o=4\;</math>, obteniendo: | sustituimos <math>m=3\;</math>, <math>x_o=-2\;</math>, <math>y_o=4\;</math>, obteniendo: | ||
| {{Caja |contenido=<math>y-4=3(x+2)\;\!</math>}} | {{Caja |contenido=<math>y-4=3(x+2)\;\!</math>}} | ||
| - | }}{{p}} | + | }} |
| - | {{AI2|titulo=Actividad Interactiva: ''Ecuación punto-pendiente''|cuerpo= | + | {{p}} |
| - | {{ai_cuerpo | + | {{Videotutoriales|titulo=Ecuación punto-pendiente de una recta|enunciado= |
| - | |enunciado=1. Halla la ecuación de la recta conocida la pendiente y un punto. | + | {{Video_enlace_khan |
| - | |actividad= | + | |titulo1=Tutorial |
| - | Como se conoce la pendiente, sólo hay que determinar la ordenada en el origen de la recta <math>y=mx+k</math>. | + | |duracion=9'20" |
| - | + | |sinopsis=Introducción a la forma punto-pendiente de la ecuación de la recta. | |
| - | <center><iframe> | + | |url1=https://youtu.be/tsv4KJ-9ais |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Funcion_afin/Caracteristicas_de_la_funcion_afin_4.html | + | }} |
| - | width=560 | + | {{Video_enlace_julioprofe |
| - | height=400 | + | |titulo1=Ejercicio 1 |
| - | name=myframe | + | |duracion=5'12" |
| - | </iframe></center> | + | |sinopsis=Determina la ecuación general de la recta que pasa por el punto (-2,3) y es paralela a la recta 2x-3y=0. |
| - | + | |url1=https://www.youtube.com/watch?v=QV-mg-WAWto&list=PL9B9AC3136D2D4C45&index=98}} | |
| - | a) Tienes que escribir el valor de <math>k</math> para determinar la ecuación de la recta que pasa por el punto amarillo y tiene de pendiente el valor indicado, <math>m</math>. | + | {{Video_enlace_abel |
| - | + | |titulo1=Ejercicio 2 | |
| - | El pulsador azul de la ayuda la activa y el rojo la desactiva. Con la ayuda activada no cuenta los aciertos. | + | |duracion=5'30" |
| - | + | |sinopsis=Halla la ecuación de la recta que pasa por el origen de coordenadas y es paralela a al recta de ecuación 2x-y+3=0. | |
| - | Si aciertas verás la expresión de la función con color naranja, si no aciertas verás la recta correspondiente de color rojizo. | + | |url1=https://youtu.be/DE7rhu10c3A?t=11m33s |
| - | + | }} | |
| - | Después de cada acierto pulsa el botón animar para que se salga una nueva recta. | + | }} |
| + | {{Actividades|titulo=Ecuación punto-pendiente de una recta|enunciado= | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 1 | ||
| + | |descripcion=Actividades en las que aprenderás obtener la ecuación punto-pendiente de una recta. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena10/3quincena10_contenidos_3a.htm | ||
| + | }} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás practicar el cálculo de la ecuación de la recta con una cierta pendiente y que pasa por un punto dado. | ||
| + | |enlace=[http://ggbm.at/u3eQs5HM Actividad 2] | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
Revisión actual
Una recta queda perfectamente determinada por su inclinación y por un punto contenido en ella. Esto nos permite dar el siguiente resultado:
Ecuación punto-pendiente
Sea 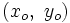 un punto de una recta y
un punto de una recta y  su pendiente, entonces su ecuación viene dada por:
su pendiente, entonces su ecuación viene dada por:
|
|
expresión que se denomina ecuación punto-pendiente de la recta.
Para comprobar que esta es la ecuación de la recta, comprobaremos que su pendiente es  y que pasa por el punto dado
y que pasa por el punto dado 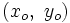 .
En efecto:
.
En efecto:
- Si desarrollamos la expresión de la ecuación punto-pendiente, se obtiene:
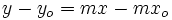
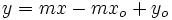
de donde se observa que el coeficiente e la x es  , y por tanto, la pendiente de la recta.
, y por tanto, la pendiente de la recta.
- Si sustituimos el punto
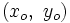 en la ecuación punto-pendiente, es decir, hacemos
en la ecuación punto-pendiente, es decir, hacemos 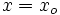 e
e 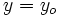 , se obtiene
, se obtiene
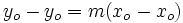
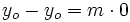
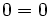
Ejemplo: Ecuación punto-pendiente
Halla la ecuación punto-pendiente de la recta que pasa por el punto (-2, 4) y tiene pendiente 3.
En la ecuación punto-pendiente:
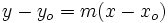
sustituimos 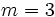 ,
, 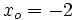 ,
, 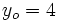 , obteniendo:
, obteniendo:
|
|
Introducción a la forma punto-pendiente de la ecuación de la recta.
Determina la ecuación general de la recta que pasa por el punto (-2,3) y es paralela a la recta 2x-3y=0.
Halla la ecuación de la recta que pasa por el origen de coordenadas y es paralela a al recta de ecuación 2x-y+3=0.
Actividades en las que aprenderás obtener la ecuación punto-pendiente de una recta.
En esta escena podrás practicar el cálculo de la ecuación de la recta con una cierta pendiente y que pasa por un punto dado.