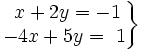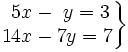Plantilla:Sistemas equivalentes
De Wikipedia
| Revisión de 20:21 31 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 2: | Línea 2: | ||
| Dos sistemas son '''equivalentes''' cuando tienen las mismas soluciones.}} | Dos sistemas son '''equivalentes''' cuando tienen las mismas soluciones.}} | ||
| {{p}} | {{p}} | ||
| + | Al igual que hicimos con las [[Ecuaciones (3ºESO Académicas)|ecuaciones]], para resolver sistemas, obtendremos otros equivalentes más sencillos de resolver que el de partida. Para ello utilizaremos las siguientes técnicas. | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Transformaciones que mantienen la equivalencia de los sistemas|enunciado= | ||
| + | |||
| + | #Si se suma o resta a ambos miembros de una ecuación de un sistema una misma expresión, el sistema resultante es equivalente. | ||
| + | #Si se multiplican o se dividen ambos miembros de un sistema por un número distinto de cero el sistema resultante es equivalente. | ||
| + | #Si se suma o resta a una ecuación del sistema otra ecuación del sistema el sistema resultante es equivalente. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Observación|texto=*Los dos primeros apartados ya los conocíamos del tema de [[Ecuaciones (3ºESO Académicas)|ecuaciones]], ya que son las transformaciones que permiten obtener ecuaciones equivalentes a una dada. | ||
| + | *Los apartados 2 y 3 se puede combinar, esto es, si a una ecuación de un sistema le sumamos o restamos otra ecuación multiplicada o dividida por un número distinto de cero, el sistema obtenido es equivalente.}} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Sistemas equivalentes|enunciado= | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=8´14" | ||
| + | |url1=https://youtu.be/5Cfqq3cOzzM | ||
| + | |sinopsis=¿Por qué podemos restar una ecuación de la otra en un sistema de ecuaciones? | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=7´14" | ||
| + | |url1=https://youtu.be/GgvyYh437ec | ||
| + | |sinopsis=Dado el sistema: | ||
| + | |||
| + | :<math>\left . \begin{matrix} ~x+2y=-1 \\ -4x+5y=~1 \end{matrix} \right \}</math> | ||
| + | |||
| + | determina cuáles de los siguientes sistemas son equivalentes al anterior: | ||
| + | |||
| + | :a) <math>\left . \begin{matrix} ~x+2y=-1 \\ -3x+7y=~0 \end{matrix} \right \}</math> | ||
| + | :b) <math>\left . \begin{matrix} -4x+~5y=1 \\ -8x-16y=8 \end{matrix} \right \}</math> | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=6´18" | ||
| + | |url1=https://youtu.be/2NG0UuzGQuU | ||
| + | |sinopsis=Dado el sistema: | ||
| + | |||
| + | :<math>\left . \begin{matrix} ~5x-~y=3 \\ 14x-7y=7 \end{matrix} \right \}</math> | ||
| + | |||
| + | determina cuáles de los siguientes sistemas son equivalentes al anterior: | ||
| + | |||
| + | :a) <math>\left . \begin{matrix} 19x-8y=10 \\ 14x-7y=~2 \end{matrix} \right \}</math> | ||
| + | :b) <math>\left . \begin{matrix} ~5x-y=-6 \\ -2x+y=-1 \end{matrix} \right \}</math> | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Sistemas equivalentes|enunciado= | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=Dado el siguiente sistema: | + | |descripcion=En esta escena podrás realizar la siguiente actividad en la que se comprueba como ciertas transformaciones hechas a un sistema dan lugar a otro sistema equivalente. |
| - | <center><math>\left . \begin{matrix} 2x-y=6 \\ 3x+3y=18 \end{matrix} \right \}</math></center> | + | Partirás del sistema: |
| - | a) Represéntalo gráficamente y anota la solución. | + | <center><math>\left . \begin{matrix} 2x-y=6 \\ 3x+3y=18 \end{matrix} \right \}</math></center> |
| - | b) Multiplica la primera ecuación por 3 y divide la segunda por 3. Representa el nuevo sistema. ¿Qué solución tiene? | + | y deberás contestar a las siguientes preguntas: |
| - | c) Resta a la 2ª ecuación la 1ª ecuación y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida. ¿Qué solución tiene?. ¿Es equivalente al sistema de partida? | + | #Este sistema está representado en la escena. ¿Cuál es su solución? |
| + | #Divide la segunda ecuación por 3, dejando la segunda ecuación igual. Representa el nuevo sistema. ¿Qué solución tiene el nuevo sistema?. ¿Es equivalente al sistema de partida? | ||
| + | #En el sistema obtenido en el apartado 2, suma la 2ª ecuación a la 1ª y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida (por ejemplo la segunda). ¿Qué solución tiene?. ¿Es equivalente al sistema de partida? | ||
| + | #En el sistema obtenido en el apartado 3, divide la primera ecuación (la que no tiene "y") por 3 y deja la segunda ecuación igual. ¿Qué solución tiene?. ¿Es equivalente al sistema de partida? | ||
| - | Pincha en el enlace para realizar la actividad. | + | Podrás hacer uso de la escena para representar las ecuaciones de los sistemas que van a apareciendo en cada apartado. |
| - | |enlace=[https://ggbm.at/EuQne8v6 Actividad: Sistemas equivalentes] | + | |enlace=[http://ggbm.at/EuQne8v6 Actividad] |
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación | ||
| + | |descripcion=Sistemas de ecuaciones equivalentes. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/equivalent-systems-of-equations/e/understanding-solution-methods-to-systems-of-equations | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
Dos sistemas son equivalentes cuando tienen las mismas soluciones.
Al igual que hicimos con las ecuaciones, para resolver sistemas, obtendremos otros equivalentes más sencillos de resolver que el de partida. Para ello utilizaremos las siguientes técnicas.
Transformaciones que mantienen la equivalencia de los sistemas
- Si se suma o resta a ambos miembros de una ecuación de un sistema una misma expresión, el sistema resultante es equivalente.
- Si se multiplican o se dividen ambos miembros de un sistema por un número distinto de cero el sistema resultante es equivalente.
- Si se suma o resta a una ecuación del sistema otra ecuación del sistema el sistema resultante es equivalente.
- Los dos primeros apartados ya los conocíamos del tema de ecuaciones, ya que son las transformaciones que permiten obtener ecuaciones equivalentes a una dada.
- Los apartados 2 y 3 se puede combinar, esto es, si a una ecuación de un sistema le sumamos o restamos otra ecuación multiplicada o dividida por un número distinto de cero, el sistema obtenido es equivalente.
¿Por qué podemos restar una ecuación de la otra en un sistema de ecuaciones?
Dado el sistema:
determina cuáles de los siguientes sistemas son equivalentes al anterior:
- a)
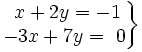
- b)
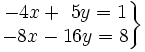
Dado el sistema:
determina cuáles de los siguientes sistemas son equivalentes al anterior:
- a)
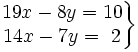
- b)
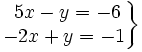
En esta escena podrás realizar la siguiente actividad en la que se comprueba como ciertas transformaciones hechas a un sistema dan lugar a otro sistema equivalente.
Partirás del sistema:
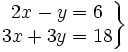
y deberás contestar a las siguientes preguntas:
- Este sistema está representado en la escena. ¿Cuál es su solución?
- Divide la segunda ecuación por 3, dejando la segunda ecuación igual. Representa el nuevo sistema. ¿Qué solución tiene el nuevo sistema?. ¿Es equivalente al sistema de partida?
- En el sistema obtenido en el apartado 2, suma la 2ª ecuación a la 1ª y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida (por ejemplo la segunda). ¿Qué solución tiene?. ¿Es equivalente al sistema de partida?
- En el sistema obtenido en el apartado 3, divide la primera ecuación (la que no tiene "y") por 3 y deja la segunda ecuación igual. ¿Qué solución tiene?. ¿Es equivalente al sistema de partida?
Podrás hacer uso de la escena para representar las ecuaciones de los sistemas que van a apareciendo en cada apartado.
Sistemas de ecuaciones equivalentes.