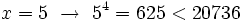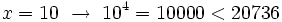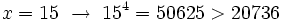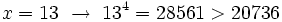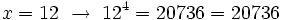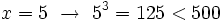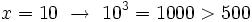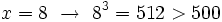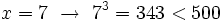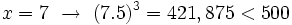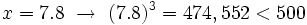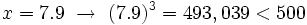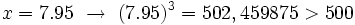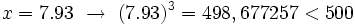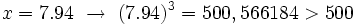Ecuaciones (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Veamos lo que recuerdas de cursos anteriores con unos problemillas para entrar en calor.
En la primera parte del siguiente videotutorial se explican las nociones básicas sobre ecuaciones:
Tutorial en el que se dan los conceptos básicos respecto a las ecuaciones y sistemas de ecuaciones.
- 00:00 a 01:40: Definición de expresión algebraica.
- 01:40 a 04:00: Definición y ejemplos de ecuaciones.
- 04:00 a 08:32: Definición y ejemplo de solución de una ecuación.
- 08:32 a 10:02: Definición de tipos de igualdades según sus soluciones.
- 10:02 a 10:48: Definición y ejemplos de sistemas de ecuaciones.
- 10:48 a 14:20: Definición y ejemplo de solución de un sistema de ecuaciones.
- 14:20 a Fin: Definición de tipos de sistema de ecuaciones según sus soluciones.
(Pág. 104)
Ecuación e identidad
En Matemáticas, cuando queremos resolver un problema, buscamos uno o varios números que cumplan las condiciones de dicho problema. Dichas condiciones suelen establecerse por medio de ecuaciones que son igualdades que relacionan las variables y números que intervienen en el problema, y que deben satisfacer los números buscados.
- Una ecuación es una igualdad entre expresiones algebraicas, en las que aparece una o más letras, llamadas incógnitas. Podemos tener ecuaciones con una incógnita, con dos incógnitas, etc.
- Las expresiones algebraicas a ambos lados de la ecuación reciben el nombre de miembros de la ecuación.
- Los términos de una ecuación son los monomios que forman cada uno de los miembros de la ecuación. Recuerda que los números pueden considerarse monomios de grado cero.
- El grado de una ecuación es el mayor de los grados de los monomios que aparecen en la ecuación una vez ésta ha sido reducida (simplificada).
- Una solución de una ecuación son los números (uno por cada incógnita) que hacen que la igualdad sea cierta, al sustituir las incógnitas por dichos números.
- Resolver una ecuación es hallar su solución o soluciones, si es que existe alguna.
- Un caso particular de ecuación es la identidad, en la que los dos lados de la igualdad son equivalentes. Por tanto, en ellas la igualdad se cumple para cualquier valor de las letras.
- Ecuaciones con una incógnita:
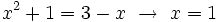 es una solución.
es una solución.
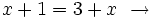 No tiene solución.
No tiene solución.
- Ecuación con dos incógnitas:
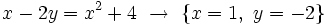 es una solución.
es una solución.
Actividades en la que aprenderás a distinguir una ecuación de una identidad.
Actividades en la que aprenderás a comprobar si un número es solución o no de una ecuación.
Ejercicios de autoevaluación sobre ecuaciones.
Tipos de ecuaciones
Hay ecuaciones de diversos tipos, dependiendo de las operaciones en las que intervienen sus incógnitas:
- Ecuaciones polinómicas: Las incógnitas son las variables de un polinomio.
- Ecuaciones radicales: Las incógnitas aparecen dentro de radicales.
- Ecuaciones racionales: Las incógnitas aparecen en los denominadores.
- Ecuaciones exponenciales: Las incógnitas aparecen como exponentes.
Ejercicios de autoevaluación sobre tipos de ecuaciones.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones |
(Pág. 105)
Ecuaciones equivalentes
Dos ecuaciones son equivalentes si tienen las mismas soluciones.
Transformaciones que mantienen la equivalencia de las ecuaciones
A partir de una ecuación podemos obtener otra equivalente si efectuamos alguna de las siguientes operaciones:
- Regla de la suma: Sumar o restar la misma expresión en los dos miembros de la igualdad. (Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.)
- Regla del producto: Multiplicar o dividir los dos miembros de la igualdad por un mismo número distinto de cero. (Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.)
Tutorial en el que se muestra como expresar cualquier ecuación en su forma general o canónica. El proceso requerirá del uso de la regla de la suma y del producto para obtener ecuaciones equivalentes cada vez más sencillas.
Ejercicios de autoevaluación sobre ecuaciones equivalentes.
Resolución de ecuaciones por tanteo
Resolver una ecuación por tanteo consiste en ir probando con distintos valores, siguiendo un procedimiento ordenado y coherente, hasta encontrar un valor que sea la solución, o bien, que esté tan cerca de ésta como se desee.
Ejercicio resuelto: Resolución de ecuaciones por tanteo
Resuelve por tanteo:
- a)
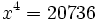
- b)
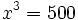
a) 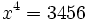
Probamos con:
Solución: 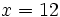
b) 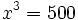
Probamos con:
Por tanto, la solución está comprendida entre 7 y 8. Seguimos aproximando a las décimas:
Por tanto, la solución está comprendida entre 7.9 y 8. Seguimos aproximando a las centésimas:
Por tanto, la solución está comprendida entre 7.93 y 7.94. Podríamos seguir aproximando a las milésimas, etc.
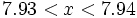 (aproximación a las centésimas)
(aproximación a las centésimas)Ejercicios propuestos
|
Ejercicios propuestos: Resolución de ecuaciones por tanteo |
Actividades
Ejercicios de autoevaluación sobre ecuaciones.
Ejercicios de autoevaluación sobre ecuaciones.
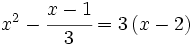 (es polinómica de grado 2)
(es polinómica de grado 2)
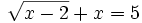 (es radical)
(es radical)
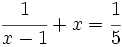 (es racional)
(es racional)
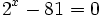 (es exponencial)
(es exponencial)