Plantilla:Polinomios
De Wikipedia
| Revisión de 09:17 12 ene 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:23 12 ene 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 149: | Línea 149: | ||
| |url1=https://www.youtube.com/watch?v=wXujh2wQNnE&index=6&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | |url1=https://www.youtube.com/watch?v=wXujh2wQNnE&index=6&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| }} | }} | ||
| - | {{Video_enlace_khan | + | {{Video_enlace_escuela |
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'13" | ||
| + | |sinopsis=7) Clasificar polinomios en homogéneos/heterogéneos. | ||
| + | |||
| + | :a) <math>4x^2+2xy</math> | ||
| + | |||
| + | :b) <math>2xy+5x-6</math> | ||
| + | |||
| + | :c) <math>5x^4+2x^2y^2</math> | ||
| + | |||
| + | :d) <math>3x^2y-2y^3+2x</math> | ||
| + | |||
| + | :e) <math>6x^3y^2+5y^3x^2+1</math> | ||
| + | |||
| + | :f) <math>6x^3y^2+5y^3x^2</math> | ||
| + | |||
| + | :g) <math>5x^3-6y^3</math> | ||
| + | |url1=https://youtu.be/A3AuZovTSQ4?list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5 | ||
| |duracion=2'46" | |duracion=2'46" | ||
| |sinopsis=Dado el polinomio <math>3x^2-8x+7\;</math>, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos. | |sinopsis=Dado el polinomio <math>3x^2-8x+7\;</math>, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos. | ||
Revisión de 09:23 12 ene 2018
Los siguientes videotutoriales condensan los conceptos que vamos a ver en este apartado sobre polinomios.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos. Valor numérico de un polinomio.
Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis. Por ejemplo: a) El polinomio b) El polinomio c) Los polinomios constantes, como por ejemplo d) Los polinomios e) Los polinomios Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes... Polinomios. Grado de un polinomio. Ejemplos. Polinomios. Grado de un polinomio. Ejemplos. Aprende a calcular el grado relativo y absoluto de un polinomio. Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio. Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio. Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio. 1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
2) Expresa en forma reducida los siguientes polinomios:
3) Indica el grado de cada polinomio:
4) Indica cuáles de estos polinomios son iguales:
5) Indica cuáles de estos polinomios son semejantes entre sí:
6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
7) Clasificar polinomios en homogéneos/heterogéneos.
Dado el polinomio Elementos y grado de un polinomio. Expresiones algebraicas: monomios y polinomios.
Actividad sobre polinomios. |
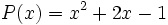
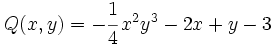
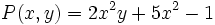 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
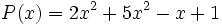 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 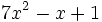 . Es de grado 2.
. Es de grado 2.
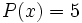 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 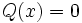 , tiene grado cero.
, tiene grado cero.
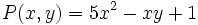 y
y 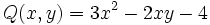 son semejantes.
son semejantes.
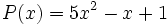 y
y 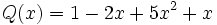 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
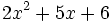
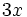
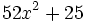
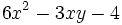
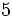
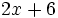
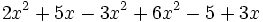
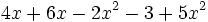
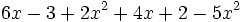
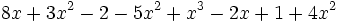
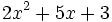 ; b)
; b) 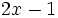 ; c)
; c) 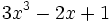
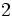 ; e)
; e) 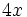 ; f)
; f) 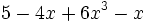
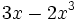 ; h)
; h) 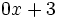 ; i)
; i) 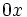
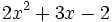 ; b)
; b) 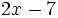 ; c)
; c) 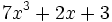 ; d)
; d) 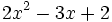
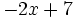 ; f)
; f) 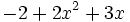 ; g)
; g) 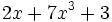 ; h)
; h) 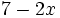
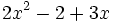 ; j)
; j) 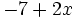 ; k)
; k) 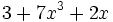 ; l)
; l) 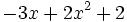
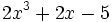 ; b)
; b) 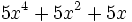 ; c)
; c) 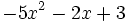
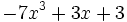 ; e)
; e) 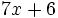 ; f)
; f) 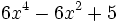
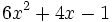 ; h)
; h) 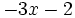
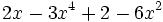
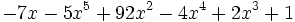
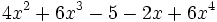
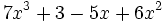
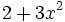
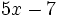
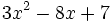 , identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.