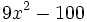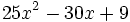Plantilla:Factorización de polinomios usando identidades notables
De Wikipedia
| Revisión de 06:26 1 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Mediante productos notables podemos transformar un polinomio en un producto de factores. | + | {{Ejemplos: Factorización de polinomios usando productos notables}} |
| - | {{Ejemplo | + | |
| - | |titulo=Ejemplos: ''Factorización de polinomios usando productos notables'' | + | |
| - | |enunciado= | + | |
| - | Factoriza: | + | |
| - | :a) <math>4x^2-9 \;\!</math> | + | |
| - | :b) <math>x^2+4x+4 \;\!</math> | + | |
| - | + | ||
| - | |sol= | + | |
| - | '''Soluciones:''' | + | |
| - | + | ||
| - | '''a)''' Al tratarse de un binomio cuyos términos están restando, sólo podemos ponerlo como diferencia de cuadrados. Extrayendo las raíces cuadradas de cada término tenemos: | + | |
| - | + | ||
| - | <math>\left . \begin{matrix}\sqrt{4x^2}=2x \\ \sqrt{9}=3 \end{matrix} \right \} \ \rightarrow \ 4x^2-9=(2x+3)(2x-3) \!</math> | + | |
| - | {{p}} | + | |
| - | ---- | + | |
| - | '''b)''' Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada: | + | |
| - | + | ||
| - | <math>\left . \begin{matrix}\sqrt{x^2}=x \\ \sqrt{4}=2 \end{matrix} \right \} \ \rightarrow \ x^2+4x+4 =(x+2)^2 \!</math> | + | |
| - | + | ||
| - | Para confirmar que esa es la factorización, comprobaremos que el doble producto del primero por el segundo es igual al otro término: | + | |
| - | + | ||
| - | :<math>2 \cdot x \cdot 2 =4x\;</math> | + | |
| - | + | ||
| - | En efecto, luego esa es la factorización. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Videotutoriales|titulo=''Factorización de polinomios usando productos notables|enunciado= | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicios 1 | + | |
| - | |duracion=4'22" | + | |
| - | |sinopsis=Factoriza: | + | |
| - | :a) <math>49x^4y^2-64w^{10}z^{14}\;</math> | + | |
| - | + | ||
| - | :b)) <math>c^8-d^8\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=tABhBMtBmSY&index=49&list=PL9B9AC3136D2D4C45 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicios 2 | + | |
| - | |duracion=4'33" | + | |
| - | |sinopsis=Factoriza: | + | |
| - | :a) <math>4x^2+12xy^2+9y^4\;</math> | + | |
| - | + | ||
| - | :b) <math>25m^4-40m^2+16\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=1dvGz8vQCeU&index=50&list=PL9B9AC3136D2D4C45 | + | |
| - | }} | + | |
| - | + | ||
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | {{Videos: Factorización de polinomios usando productos notables}} | ||
| {{Ejercicios videotutoriales identidades}} | {{Ejercicios videotutoriales identidades}} | ||
| - | + | {{Actividades: Factorización de polinomios usando productos notables}} | |
| - | {{wolfram desplegable|titulo=Factorización de polinomios mediante productos notables|contenido= | + | {{Wólfram: Factorización de polinomios mediante productos notables}} |
| - | {{wolfram | + | |
| - | |titulo=Actividad: ''Factorización de polinomios mediante productos notables'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | :Factoriza: | + | |
| - | + | ||
| - | :a) <math>9x^2-100\!</math> | + | |
| - | :b) <math>25x^2-30x+9\!</math> | + | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) {{consulta|texto=factor 9x^2-100}} | + | |
| - | :b) {{consulta|texto=factor 25x^2-30x+9}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión actual
Las identidades notables son útiles para completar ciertas operaciones de forma rápida, pero una de sus aplicaciones más interesantes consiste en hacer lo contrario, deshacer cuentas. Son una potente herramienta para la descomposición y simplificación de expresiones algebraicas.
Ejemplos: Factorización de polinomios usando productos notables
Factoriza:
- a)
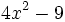
- b)
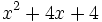
Soluciones:
a) Al tratarse de un binomio cuyos términos están restando, sólo podemos ponerlo como diferencia de cuadrados. Extrayendo las raíces cuadradas de cada término tenemos:
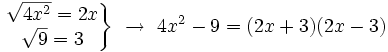
b) Al tratarse de un trinomio, buscaremos dos de sus términos que sean cuadrados perfectos y calcularemos su raíz cuadrada:
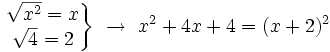
Para confirmar que esa es la factorización, comprobaremos que el doble producto del primero por el segundo es igual al otro término:
Factorización de polinomios usando productos notables. Ejemplos.
Factorización de polinomios usando productos notables. Ejemplos.
Factorización de polinomios usando el trinomio cuadrado perfecto.
Hasta el minuto 1'53": Factorización de polinomios usando diferencias de cuadrado.
Factoriza los siguientes polinomios en producto de factores usando identidades notables:
- 3a)
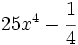
- 3b)
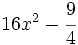
- 3c)
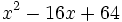
- 3d)
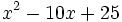
Factoriza los siguientes polinomios en producto de factores usando identidades notables:
- 3e)
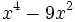
- 3f)
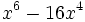
- 3g)
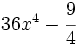
Encuentra un binomio factor común de los polinomios siguientes: 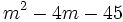 y
y 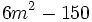
Encuentra un binomio factor común de los polinomios siguientes: 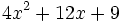 y
y 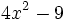
Factoriza: 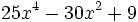
Factoriza: 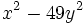
Factoriza: 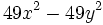
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza los siguientes polinomos usando diferencias de cuadrados:
Factoriza:
Factoriza: Factoriza: Factoriza: |
Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: | Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza: Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza los siguientes polinomios usando trinomios cuadrado perfecto:
Factoriza:
Factoriza: Factoriza: Factoriza: Factoriza: Averigua el valor de "c" y "d" de manera que Averigua el valor de "c" y "d" de manera que |
Factoriza: 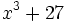
Factoriza: 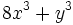
Factoriza: 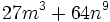
Diferencias de cuadrados:
Factorizar expresiones cuadráticas: diferencia de cuadrados
Factorizar expresiones cuadráticas: diferencia de cuadrados (Introducción)
Factorizar expresiones cuadráticas: diferencia de cuadrados
Trinomios cuadrados perfectos:
Factorizar expresiones cuadráticas: cuadrados perfectos
Factorizar expresiones cuadráticas: cuadrados perfectos
Productos notables:
Factoriza polinomios: formas de productos notables
Factoriza polinomios: formas de productos notables
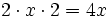
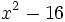
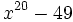
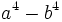
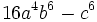
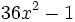
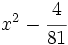
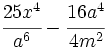
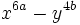
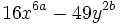
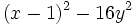
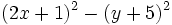
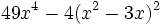
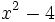
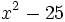

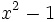
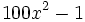
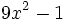
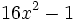
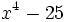
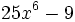
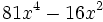
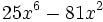
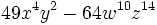
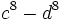
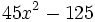
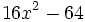

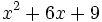
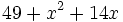
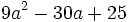

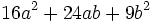
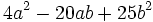
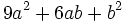
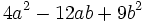
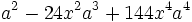
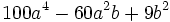
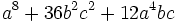
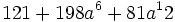
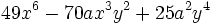
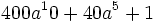
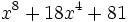
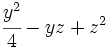
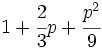
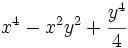
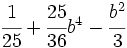
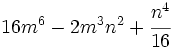
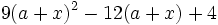
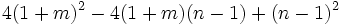
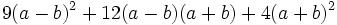
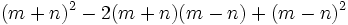
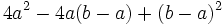
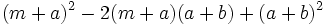
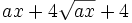
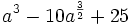
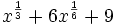
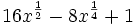
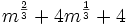
![\sqrt[3]{m^2}-6\sqrt[3]{m}+9\;](/wikipedia/images/math/a/2/a/a2a527f84cd9528ace07b344292c0c0b.png)
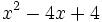
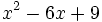
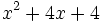
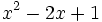
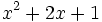

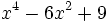
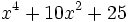
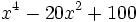
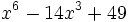
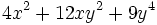
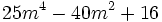
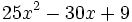
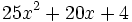
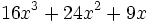
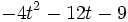
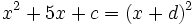 .
.