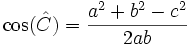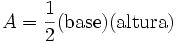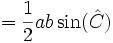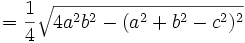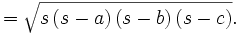Plantilla:Area triangulo
De Wikipedia
| Revisión de 10:59 20 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 83: | Línea 83: | ||
| {{Actividades|titulo=Área y perímetro del triángulo|enunciado= | {{Actividades|titulo=Área y perímetro del triángulo|enunciado= | ||
| {{AI_anaya | {{AI_anaya | ||
| - | |titulo1=Actividad 1: ''Del triángulo al rectángulo'' | + | |titulo1=Actividad 1 |
| |descripcion= | |descripcion= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/13/03.htm | + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/13/03.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| Línea 93: | Línea 93: | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/13/03.htm | + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/13/03.htm |
| }} | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás deducir la fórmula del área del triángulo. | |descripcion=En esta escena podrás deducir la fórmula del área del triángulo. | ||
| - | |enlace=[http://ggbm.at/mwSJZbYS Actividad 2: ''Deduciendo el área del triángulo''] | + | |enlace=[http://ggbm.at/mwSJZbYS Actividad 2] |
| }} | }} | ||
| {{AI_anaya | {{AI_anaya | ||
| - | |titulo1=Actividad 3: ''Área y perímetro del triángulo'' | + | |titulo1=Actividad 3 |
| |descripcion=Ejercicios de autoevaluación sobre el área y el perímetro de triángulos. | |descripcion=Ejercicios de autoevaluación sobre el área y el perímetro de triángulos. | ||
| |url1=http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud12/3/03.htm | |url1=http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud12/3/03.htm | ||
Revisión actual
|
|
Videotutorial que condensa todo lo que vamos a ver sobre medidas en los triángulos.
Fórmula general y tres casos prácticos de cómo calcular el área de un triángulo.
Deducción del área de un triángulo.
Deduciendo la fórmula del área del triángulo.
Demostración de área del triángulo.
Calcula la altura de un triángulo de 34 cm2 de área y 10 cm de base.
El área de un triángulo isósceles es de 24 dm2. Si sabemos que la altura relativa al lado desigual es de 100 cm, ¿cuántos cm mide este lado?
Calcula el área de un triángulo equilátero de 7 cm de lado.
Calcula el la altura, el área y el perímetro de un triángulo isósceles de 8 cm de base y cuyos lados iguales miden 7 cm.
Calcula el área de un triángulo equilátero de 36 m de perímetro.
En esta escena podrás deducir la fórmula del área del triángulo.
Ejercicios de autoevaluación sobre el área y el perímetro de triángulos.
Actividades sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Ejercicios de autoevaluación sobre el área del triángulo.
Fórmula de Herón
Nota: El nivel de esta demostración corresponde a 1º de Bachillerato.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados  ,
,  ,
,  , cuyos ángulos opuestos a cada uno de esos lados son
, cuyos ángulos opuestos a cada uno de esos lados son 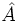 ,
, 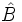 ,
, 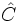 .
.
Por el teorema del coseno, tenemos que:
Por la relación fundamental de la trigonometría, tenemos que:
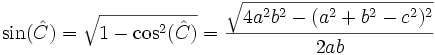 .
.
La altura de un triángulo de base  tiene una longitud
tiene una longitud 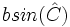 , por tanto siguiendo con la demostración
, por tanto siguiendo con la demostración
En esta escena podrás calcular el área de un triángulo mediante la fórmula de Herón.
Determinar el área y el perímetro de un triángulo cuyos lados miden 3, 4 y 5.
Determinar el área y el perímetro de un triángulo cuyos lados miden 4.4, 6.7 y 9.3.
Determinar el área y el perímetro de un triángulo rectángulo cuyos catetos miden 24 cm y 7 cm.
|
Actividad: El triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|

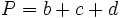
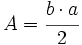
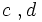 : lados.
: lados.
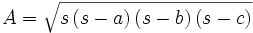
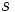 es el semiperímetro:
es el semiperímetro: 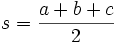 .
.