Plantilla:Valor absoluto (1º Bach)
De Wikipedia
| Revisión de 07:27 1 sep 2016 Coordinador (Discusión | contribuciones) (→Ejemplos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | == Valor absoluto de un número real == | + | {{Caja_Amarilla|texto=El '''valor absoluto''' o '''módulo''' de un número real <math>a\;</math> es el propio número <math>a\;</math>, si es positivo o nulo. Y su opuesto, <math>-a\;</math>, si es negativo. Es decir: |
| - | (pág. 30) | + | |
| - | + | ||
| - | {{Caja_Amarilla|texto=El '''valor absoluto''' o '''módulo''' de un número real <math>a\;</math> es el propio número <math>a\;</math>, si es positivo, o su opuesto, <math>-a\;</math>, si es negativo. Es decir: | + | |
| <center><math>|a| = \begin{cases} | <center><math>|a| = \begin{cases} | ||
| - | \;\;\;a, & \mbox{si } a \ge 0\\ | + | \;\;\;a \, , & \mbox{si } a \ge 0\\ |
| - | -a, & \mbox{si } a < 0 | + | -a\, , & \mbox{si } a < 0 |
| \end{cases} </math></center> | \end{cases} </math></center> | ||
| }} | }} | ||
| - | Nótese que el valor absoluto de un número siempre será positivo. Desde un punto de vista geométrico, el valor absoluto de un número real <math>a\;</math> corresponde a la distancia a lo largo de la recta real desde <math>a\;</math> hasta el cero. | ||
| {{p}} | {{p}} | ||
| - | {{Reglas desigualdades}} | + | Desde un punto de vista geométrico, el valor absoluto de un número real <math>a\;</math> corresponde a la [[Números reales (1ºBach)#Distancia |distancia]] a lo largo de la recta real desde <math>a\;</math> hasta el cero. |
| - | {{p}} | + | {{Ejemplo_simple|titulo=Ejemplos: |
| - | + | |contenido={{Ejemplo|titulo=Ejemplos: ''Valor absoluto'' | |
| - | (pág. 30) | + | |
| - | {{Ejemplo|titulo=Ejercicios resueltos: ''Valor absoluto'' | + | |
| |enunciado= | |enunciado= | ||
| - | ::'''1)''' Calcula el valor absoluto de los siguientes números: <math>7.4,~0,~-5.87,~\sqrt{9},~1-\sqrt{3}</math> | + | '''1)''' Calcula el valor absoluto de los siguientes números: <math>7.4,~0,~-5.87,~\sqrt{9},~1-\sqrt{3}</math> |
| - | ::'''2)''' ¿Para qué valores de x se cumplen las siguientes expresiones? | + | '''2)''' ¿Para qué valores de x se cumplen las siguientes expresiones? |
| - | :::a) <math>|x|=3\;</math> | + | :a) <math>|x|=3\;</math> |
| - | :::b) <math>|x|=0\;</math> | + | :b) <math>|x|=0\;</math> |
| - | :::c) <math>|x|=\sqrt{3}\;</math> | + | :c) <math>|x|=\sqrt{3}\;</math> |
| - | + | ||
| - | ::'''3)''' ¿Para qué valores de x se cumplen las siguientes desigualdades? | + | |
| - | :::b) <math>|x|<3\;</math> | + | |
| - | + | ||
| - | :::b) <math>|x| \ge 3\;</math> | + | |
| - | + | ||
| - | :::c) <math>|x-2|\le 3\;</math> | + | |
| |sol= | |sol= | ||
| Línea 44: | Línea 31: | ||
| :b) <math>|x|=0 \iff x=0 </math> | :b) <math>|x|=0 \iff x=0 </math> | ||
| :c) <math>|x|= \sqrt{3} \iff x= \sqrt{3} \quad \acute{o} \quad x=-\sqrt{3}</math> | :c) <math>|x|= \sqrt{3} \iff x= \sqrt{3} \quad \acute{o} \quad x=-\sqrt{3}</math> | ||
| - | '''3)''' | + | |
| - | :a) <math>|x|<3 \iff -3<x<3 \iff x \in \left ( -3, 3 \right )</math> | + | }} |
| - | :b) <math>|x| \ge 3 \iff x \le-3 \quad \acute{o} \quad x \ge 3 \iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right ) </math> | + | |
| - | :c) <math>|x-2|\le 3 \iff -3<x-2<3 \iff -3+2<x-2+2<3+2 \iff -1<x<5 \iff x \in \left [ -1 , 5 \right ]</math> | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{wolfram | + | {{AI_cidead |
| - | |titulo=Actividad: ''Valor absoluto'' | + | |titulo1=Actividades: ''Valor absoluto'' |
| - | |cuerpo= | + | |descripcion=Valor absoluto de un número real. Ejemplos y actividades. |
| - | {{ejercicio_cuerpo | + | |url1=http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/reales/quincena1_contenidos_3b.htm |
| - | |enunciado= | + | }} |
| + | {{p}} | ||
| + | ===Propiedades del valor absoluto=== | ||
| + | {{Teorema_sin_demo|titulo= Propiedades del valor absoluto|enunciado= | ||
| + | :'''1.'''{{b}} <math>|x|>0 \, ,\; \forall x \ne 0</math> | ||
| - | : Resuelve | + | :'''2. '''{{b}} <math>\forall k>0 \, , \, \ |x|=k \iff x=k \ \ \or \ \ x=-k</math> |
| - | ::a) <math>|3x-1|=0 \;</math> | + | |
| - | ::b) <math>|3x-1|=4 \;</math> | + | :'''3. '''{{b}} <math>\forall k>0 \, , \, \ |x|<k \iff -k < x < k</math> |
| - | ::c) <math>|x-5|>2 \;</math> | + | :'''4. '''{{b}} <math>\forall k>0 \, , \, \ |x|>k \iff x>k \ \ \or \ \ x<-k</math> |
| + | :'''5. '''{{b}} <math>|x \cdot y|= |x| \cdot |y|</math> | ||
| - | {{p}} | + | :'''6. '''{{b}} <math>\forall n \in \mathbb{N} \, , \, \ |x^n|= |x|^n</math> |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | :a) <math>|3x-1|=0</math> | + | :'''7. '''{{b}} <math>\left| \cfrac{x}{y} \right|= \cfrac{|x|}{|y|}</math> |
| - | :b) <math>|3x-1|=4</math> | + | |
| - | :c) <math>|x-5|>2</math> | + | |
| + | :'''8. '''{{b}} <math>|x^2| = x^2\;</math> | ||
| - | {{widget generico}} | + | :'''9. '''{{b}} <math>|x + y| \le |x|+|y|</math> (desigualdad triangular) |
| - | }} | + | |
| + | :'''10. '''{{b}} <math>|x - y| \le |x|+|y|</math> | ||
| + | |||
| + | :'''11. '''{{b}} <math>|x| - |y| \le |x-y|</math> | ||
| + | |||
| + | :'''12. '''{{b}} <math>\left| |x| - |y| \right| \le |x-y|</math> | ||
| }} | }} | ||
| + | {{Videotutoriales|titulo=Valor absoluto de un número real. Propiedades|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=13´53" | ||
| + | |sinopsis=Tutorial en el que se explica y trabaja el concepto matemático de valor absoluto de un número real y expresiones sencillas. | ||
| - | ==Videotutoriales== | + | *00:00 a 03:25: Definición matemática de valor absoluto y ejemplos iniciales. |
| - | {{Video_enlace2 | + | *03:25 a 11:10: Cálculo del valor absoluto de expresiones numéricas sencillas. |
| - | |titulo1=Valor absoluto de un número real | + | *11:10 a 13:53: Propiedades del Valor Absoluto. |
| + | |url1=https://www.youtube.com/watch?v=zI7WbIu9p2w&index=5&list=PLZNmE9BEzVIldr5sFGtnV3nRU974wLtCK | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 2 | ||
| |duracion=2´47" | |duracion=2´47" | ||
| |sinopsis= | |sinopsis= | ||
| Línea 88: | Línea 87: | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/08-valor-absoluto-de-un-numero-real-4#.VCVb2hZ8HA8 | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/08-valor-absoluto-de-un-numero-real-4#.VCVb2hZ8HA8 | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_matefacil |
| - | {{Video_enlace2 | + | |titulo1=Tutorial 3 |
| - | |titulo1=Distancia entre dos puntos | + | |duracion=8´36" |
| - | |duracion=3'31" | + | |
| |sinopsis= | |sinopsis= | ||
| - | *Definición de distancia entre dos puntos de la recta real: <math>d(x,y)=|x-y|~,~ \forall x, y \in \mathbb{R}</math> | + | *Definición del valor absoluto de un número. |
| *Ejemplos. | *Ejemplos. | ||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/09-distancia-entre-dos-puntos-4#.VCVb-BZ8HA8 | + | *Propiedades del valor absoluto. |
| + | |url1=https://www.youtube.com/watch?v=4KY4yOOAPSg | ||
| }} | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 3 (demostración) | ||
| + | |duracion=8´33" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| - | ==Ejercicios== | + | :<math>\forall k>0 \, , \, \ |x|<k \iff -k < x < k</math> |
| - | (pág. 30) | + | |
| - | {{ejercicio | + | |url1=https://www.youtube.com/watch?v=qVKeVZV425k |
| - | |titulo=Ejercicios propuestos: ''Valor absoluto'' | + | }} |
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 5 (demostración) | ||
| + | |duracion=7´38" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | :<math>|x \cdot y|= |x| \cdot |y|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=greulfXIvbw | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 6 (demostración) | ||
| + | |duracion=2´53" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | :<math>\forall n \in \mathbb{N} \, , \, \ |x^n|= |x|^n</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rnlQRQSzK9E | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 7 (demostración) | ||
| + | |duracion=2´11" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | :<math>\left| \cfrac{x}{y} \right|= \cfrac{|x|}{|y|}</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=4ElOW7rw5SE | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 8 (demostración) | ||
| + | |duracion=3´15" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x^2\=x^2\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=qvKAtO-HEic&index=8&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 9 (demostración) | ||
| + | |duracion=12´36" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x + y| \le |x|+|y|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=KconocgQmnc&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=15 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 9 (demostración 2) | ||
| + | |duracion=4´33" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x + y| \le |x|+|y|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=ruVkE5zarTk&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=16 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 9 (demostración 3) | ||
| + | |duracion=3´22" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x + y| \le |x|+|y|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=yMfpEyU2i4U&index=17&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 10 (demostración) | ||
| + | |duracion=1´43" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x - y| \le |x|+|y|\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=VtzMI43LrFo&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=19 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 11 (demostración) | ||
| + | |duracion=1´43" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>|x|- |y| \le |x-y|\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=YBzsb9S00nY&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=20}} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad nº 12 (demostración) | ||
| + | |duracion=4´56" | ||
| + | |sinopsis=Demostración de la propiedad: | ||
| + | |||
| + | : <math>\left| |x| - |y| \right| \le |x-y|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=UGcBRiIr5mM&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=21 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad: ''La media geométrica es menor que la aritmética'' (demostración) | ||
| + | |duracion=7´24" | ||
| + | |sinopsis=Demostración de la propiedad: "La media geométrica es menor que la aritmética" | ||
| + | |||
| + | : <math>0<a<b \rightarrow a< \sqrt{ab} < \frac{a+b}{2} < b</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=qCEfJTvN8qM&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=18 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Propiedad: ''Desigualdad triangular generalizada'' (demostración) | ||
| + | |duracion=2´35" | ||
| + | |sinopsis=Demostración de la propiedad: "Desigualdad triangular generalizada" | ||
| + | |||
| + | : <math>|x_1+x_2+ \cdots + x_n| \le |x_1|+|x_2|+ \cdots + |x_n|</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=XDJm2KXY9po&list=PL9SnRnlzoyX2TEPnbgyH8Oeuuj2KrtUds&index=23 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Reglas desigualdades}} | ||
| + | {{p}} | ||
| + | |||
| + | ===Ecuaciones con valor absoluto=== | ||
| + | {{Ecuaciones con valor absoluto}} | ||
| + | {{wolfram desplegable|titulo=Valor absoluto|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Valor absoluto'' | ||
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | {{b4}}[[Imagen:yellow_star.png|12px]]'''1.''' Halla los siguientes valores absolutos: | ||
| - | {{b4}}{{b4}}'''a)''' <math>|-11| \; </math>{{b4}}'''b)''' <math>|\pi| \;</math>{{b4}}'''c)''' <math>|-\sqrt{5}| \;</math> | + | Resuelve |
| + | :a) <math>|3x-1|=0 \;</math> | ||
| - | {{b4}}{{b4}}'''d)''' <math>|0| \; </math>{{b4}}'''e)''' <math>|3-\pi| \;</math>{{b4}}'''f)''' <math>|3-\sqrt{2}| \;</math> | + | :b) <math>|3x-1|=4 \;</math> |
| - | {{b4}}{{b4}}'''g)''' <math>|1-\sqrt{2}| \; </math>{{b4}}'''h)''' <math>|\sqrt{2}-\sqrt{3}| \;</math>{{b4}}'''i)''' <math>|7-\sqrt{50}| \;</math> | + | :c) <math>|x-5|>2 \;</math> |
| - | {{b4}}[[Imagen:red_star.png|12px]]'''2.''' Averigua para qué valores de x se cumplen las siguientes relaciones: | ||
| - | {{b4}}{{b4}}'''a)''' <math>|x|=5 \; </math>{{b4}}'''b)''' <math>|x| \le 5 \;</math>{{b4}}'''c)''' <math>|x-4|=2 \;</math> | + | {{p}} |
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | a) <math>|3x-1|=0</math> | ||
| + | |||
| + | b) <math>|3x-1|=4</math> | ||
| + | |||
| + | c) <math>|x-5|>2</math> | ||
| - | {{b4}}{{b4}}'''d)''' <math>|x-4| \le 2 \; </math>{{b4}}'''e)''' <math>|x-4| > 2 \;</math>{{b4}}'''f)''' <math>|x+4|>5 \;</math> | ||
| - | |sol=Utiliza Wolfram para comprobar las soluciones: | ||
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | (pág. 33) | ||
| + | {{p}} | ||
| + | ===Inecuaciones con valor absoluto=== | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para resolver inecuaciones con valor absoluto utilizaremos las propiedades 3ª y 4ª del valor absoluto, que dicen: | ||
| + | |||
| + | *{{b}} <math>\forall k>0 \, , \, \ |x|<k \iff -k < x < k</math> | ||
| + | |||
| + | *{{b}} <math>\forall k>0 \, , \, \ |x|>k \iff x>k \ \ \or \ \ x<-k</math> | ||
| + | |||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejercicios resueltos: ''Valor absoluto'' | ||
| + | |enunciado= | ||
| + | |||
| + | ¿Para qué valores de x se cumplen las siguientes desigualdades? | ||
| + | :a) <math>|x| \ge 3\;</math> | ||
| + | |||
| + | :b) <math>|x-2|\le 3\;</math> | ||
| + | |||
| + | |sol= | ||
| + | a) <math>|x| \ge 3 \iff x \le-3 \quad \acute{o} \quad x \ge 3 \iff</math> | ||
| + | |||
| + | :<math>\iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right ) </math> | ||
| + | |||
| + | b) <math>|x-2|\le 3 \iff -3 \le x-2 \le 3 \iff -3+2 \le x-2+2 \le 3+2 \iff</math> | ||
| + | :<math> \iff -1 \le x \le 5 \iff x \in \left [ -1 , 5 \right ]</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Inecuaciones con valores absolutos}} | ||
| + | |||
| + | ===Actividades=== | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación: ''Valor absoluto'' | ||
| + | |descripcion=Ejercicios de autoevaluación sobre valor absoluto de un número real. | ||
| + | |url1=http://www.vitutor.com/di/re/r6e.html | ||
| }} | }} | ||
Revisión actual
El valor absoluto o módulo de un número real  es el propio número
es el propio número  , si es positivo o nulo. Y su opuesto,
, si es positivo o nulo. Y su opuesto, 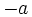 , si es negativo. Es decir:
, si es negativo. Es decir:
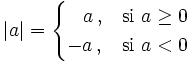
Desde un punto de vista geométrico, el valor absoluto de un número real  corresponde a la distancia a lo largo de la recta real desde
corresponde a la distancia a lo largo de la recta real desde  hasta el cero.
hasta el cero.
Valor absoluto de un número real. Ejemplos y actividades.
Tabla de contenidos |
Propiedades del valor absoluto
Tutorial en el que se explica y trabaja el concepto matemático de valor absoluto de un número real y expresiones sencillas.
- 00:00 a 03:25: Definición matemática de valor absoluto y ejemplos iniciales.
- 03:25 a 11:10: Cálculo del valor absoluto de expresiones numéricas sencillas.
- 11:10 a 13:53: Propiedades del Valor Absoluto.
- Definición del valor absoluto de un número.
- Ejemplos.
- Propiedades del valor absoluto.
- Definición del valor absoluto de un número.
- Ejemplos.
- Propiedades del valor absoluto.
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
- No se pudo entender (error de léxico): |x^2\=x^2\;
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad:
Demostración de la propiedad: "La media geométrica es menor que la aritmética"
Demostración de la propiedad: "Desigualdad triangular generalizada"
Como consecuencia, en una inecuación:
- Lo que está sumando en un lado de la desigualdad, pasa restando al otro miembro sin afectar a la desigualdad. Y viceversa.
- Lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. En este caso la desigualdad sólo cambia de sentido si el número que pasa multiplicando o dividiendo es negativo.
¿Cuándo debe cambiar de sentido una desigualdad?. Ejemplos.
Ecuaciones con valor absoluto
Procedimiento
Para resolver ecuaciones con valor absoluto utilizaremos la 2ª de las propiedades del valor absoluto, que dice:
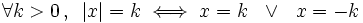
Resuelve:
a) 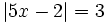
b) 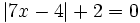
c) 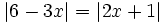
Resuelve:
a) 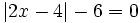
b) 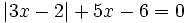
c) 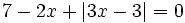
Resuelve:
Resuelve:
(pág. 33)
Inecuaciones con valor absoluto
Procedimiento
Para resolver inecuaciones con valor absoluto utilizaremos las propiedades 3ª y 4ª del valor absoluto, que dicen:
Ejercicios resueltos: Valor absoluto
¿Para qué valores de x se cumplen las siguientes desigualdades?
- a)
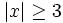
- b)
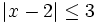
a) 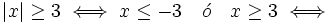
b) 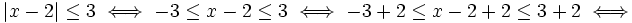
Inecuaciones con valor absoluto. Ejemplos.
Inecuaciones con valor absoluto. Ejemplos.
Resuelve:
- a)
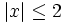
- b)
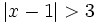
Resuelve: 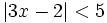
Resuelve: 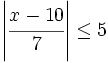
Resuelve: 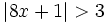
Resuelve: 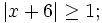
Resuelve: 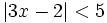
Resuelve:
a) 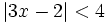
b) 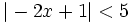
Resuelve: 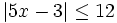
Resuelve: 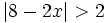
Resuelve: 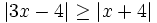
Resuelve: 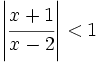
Actividades
Ejercicios de autoevaluación sobre valor absoluto de un número real.
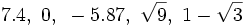
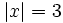
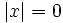
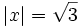
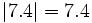
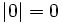
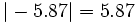
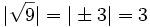
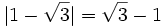
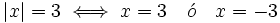
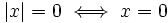
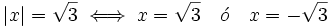
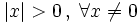
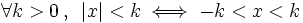
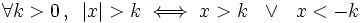
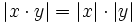
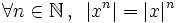
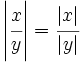
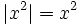
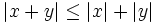 (desigualdad triangular)
(desigualdad triangular)
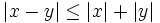
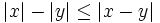
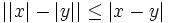
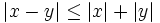
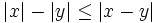
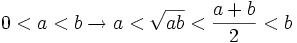
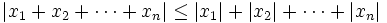
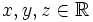 , se cumplen las siguientes propiedades:
, se cumplen las siguientes propiedades:
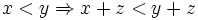
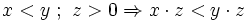
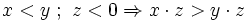
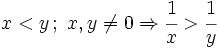
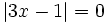
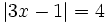
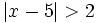
![\iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right )](/wikipedia/images/math/7/8/c/78cd6dc5f9f2acad4c05dfc30174e0c9.png)
![\iff -1 \le x \le 5 \iff x \in \left [ -1 , 5 \right ]](/wikipedia/images/math/c/4/1/c41d22d69800fc9c4f7918de0410c4f4.png)

