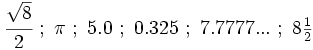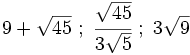Plantilla:Irracionales. Definicion
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:00 10 sep 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:16 14 sep 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| |titulo1=Tutorial | |titulo1=Tutorial | ||
| |duracion=4´57" | |duracion=4´57" | ||
| - | |url1=https://www.youtube.com/watch?v=yWU45lJ3JR8 | + | |url1=http://www.youtube.com/watch?v=yWU45lJ3JR8 |
| |sinopsis=Aquí se habla un poco sobre algunos números extraños. Aunque no son tan extraños tampoco. | |sinopsis=Aquí se habla un poco sobre algunos números extraños. Aunque no son tan extraños tampoco. | ||
| }} | }} | ||
| Línea 25: | Línea 25: | ||
| :<math>\cfrac{\sqrt{8}}{2} \ ; \ \pi \ ; \ 5.0 \ ; \ 0.325 \ ; \ 7.7777... \ ; \ 8 \begin{matrix} \frac{1}{2} \end{matrix}</math> | :<math>\cfrac{\sqrt{8}}{2} \ ; \ \pi \ ; \ 5.0 \ ; \ 0.325 \ ; \ 7.7777... \ ; \ 8 \begin{matrix} \frac{1}{2} \end{matrix}</math> | ||
| - | |url1=https://youtu.be/5B_KPhjXin8 | + | |url1=http://youtu.be/5B_KPhjXin8 |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 33: | Línea 33: | ||
| :<math>9+\sqrt{45} \ ; \ \cfrac{\sqrt{45}}{3\sqrt{5}} \ ; \ 3\sqrt{9}</math> | :<math>9+\sqrt{45} \ ; \ \cfrac{\sqrt{45}}{3\sqrt{5}} \ ; \ 3\sqrt{9}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=cDhQTkouNkQ | + | |url1=http://www.youtube.com/watch?v=cDhQTkouNkQ |
| }} | }} | ||
| }} | }} | ||
Revisión de 06:16 14 sep 2018
El conjunto de los números irracionales es el formado por aquellos números que no se pueden expresar mediante fracciones y, por tanto, cuya expresión decimal tiene infinitas cifras no periódicas. Lo representaremos con la letra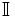 
.
Son números irracionales:
- La raíces cuadradas no exactas de números enteros como
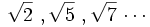
- Número famosos como el número pi, el número e o el número de oro Φ:
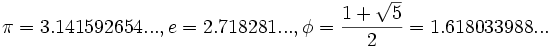
- Números con un patrón que no sea periódico: 5,123456789101112..., 8,12112111211112...
Tutorial (4´57") Sinopsis: Aquí se habla un poco sobre algunos números extraños. Aunque no son tan extraños tampoco.
Ejercicio 1 (1´44") Sinopsis: ¿Cuáles de los siguientes números son irracionales?
Ejercicio 2 (4´05") Sinopsis: ¿Cuáles de los siguientes números son irracionales?
Actividad Descripción: Actividades sobre números irracionales.
Autoevaluación Descripción: Clasifica en números racionales o irracionales.
