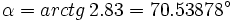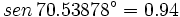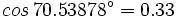Trigonometría con calculadora (1ºBach)
De Wikipedia
| Revisión de 15:48 29 jun 2017 Coordinador (Discusión | contribuciones) (→Funciones trigonométricas (recíprocas)) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Funciones trigonométricas recíprocas) |
||
| Línea 8: | Línea 8: | ||
| {{p}} | {{p}} | ||
| (Pág. 109) | (Pág. 109) | ||
| - | ==Funciones trigonométricas (recíprocas)== | + | ==Funciones trigonométricas== |
| - | Estas funciones de la calculadora nos permiten obtener el las razones trigonométricas de un ángulo. | + | {{Funciones trigonometricas con calculadora}} |
| {{p}} | {{p}} | ||
| - | {{Casio FX-100MS Trigonométricas}} | ||
| - | {{p}} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=3 ejercicios (Hallamos razones trigonométricas con la calculadora) | ||
| - | |duracion=9´42" | ||
| - | |url1=https://www.youtube.com/watch?v=fw69XASN9-g&index=5&list=PLACC8661F6A8A59FA | ||
| - | |sinopsis=En este vídeo aprendemos a emplear la calculadora científica para determinar las razones trigonométricas de un ángulo, ya esté expresado en el sistema sexagesimal o en el sistema circular. | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Funciones trigonométricas (recíprocas)== | ||
| - | Estas funciones de la calculadora nos permiten obtener el ángulo a partir del valor de una razón trigonométrica. | ||
| - | {{p}} | ||
| - | {{Casio FX-100MS Trigonométricas arco}} | ||
| - | {{p}} | ||
| - | {{Casio FX100-MS Angulos de decimal a grados}} | ||
| - | {{p}} | ||
| - | {{wolfram desplegable|titulo=Trigonometría con calculadora|contenido= | ||
| - | {{wolfram | ||
| - | |titulo=Actividad: ''Trigonometría con calculadora'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | |||
| - | '''Directas:''' | ||
| - | :a) seno 30º , b) cos 45º , c) tan 60º | ||
| - | |||
| - | '''Inversas:''' | ||
| - | :d) cosec 30º , e) cot 45º , f) sec 60º | ||
| - | |||
| - | '''Recíprocas:''' | ||
| - | :g) arcsen (0.5) , h) arccos (0.12) , arctan (2.43) | ||
| - | {{p}} | ||
| - | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | |||
| - | :a) {{consulta|texto=sin(30º)}} , b) {{consulta|texto=cos(45º)}} , c) {{consulta|texto=tan(60º)}} | ||
| - | :d) {{consulta|texto=csc(30º)}} , e) {{consulta|texto=cot(45º)}} , f) {{consulta|texto=sec(60º)}} | ||
| - | :d) {{consulta|texto=arcsin(0.5) in deg}} , e) {{consulta|texto=arccos(0.12) in deg}} , f) {{consulta|texto=arctan(2.43) in deg}} | ||
| - | |||
| - | {{widget generico}} | ||
| - | }} | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás ver como a partir del valor de una razón trigonométrica existen dos ángulos menores de 360º que tienen dicho valor. | ||
| - | |enlace=[https://ggbm.at/XUy4Ct5z Ángulos con una razón trigonométrica dada] | ||
| - | }} | ||
| - | |||
| - | {{p}} | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejercicio resuelto: ''Trigonometría con calculadora'' | ||
| - | |enunciado= | ||
| - | '''1.''' Calcula <math>sen \, \alpha</math> y <math>cos \, \alpha</math> con la calculadora, sabiendo que <math>tg \, \alpha = 2.83</math> y que <math>0^\circ < \alpha < 90^\circ</math> | ||
| - | |sol= | ||
| - | Primero se halla en ángulo: | ||
| - | |||
| - | :<math>\alpha = arctg \, 2.83 = 70.53878^\circ</math> | ||
| - | |||
| - | Con ese valor se calcula: | ||
| - | |||
| - | :<math>sen \, 70.53878^\circ = 0.94</math> | ||
| - | |||
| - | :<math>cos \, 70.53878^\circ = 0.33</math> | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=6 ejercicios (Conocida una razón trigonométrica, calcular el ángulo) | ||
| - | |duracion=8´32" | ||
| - | |url1=https://www.youtube.com/watch?v=Vdh-YenSkc0&index=6&list=PLACC8661F6A8A59FA | ||
| - | |sinopsis=En este vídeo conocemos una de las seis razones trigonométricas de un ángulo y empleamos la calculadora científica para determinar el ángulo en cuestión en el sistema sexagesimal (sólo calcula uno de los dos ángulos posibles). | ||
| - | |||
| - | }} | ||
| - | {{Videotutoriales|titulo=Determinación del ángulo conocida una de sus razones|enunciado= | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Tutorial | ||
| - | |duracion=7´38 | ||
| - | |url1=https://www.youtube.com/watch?v=5XSaseUwr88&list=PL8C0D37B1235315C7&index=7 | ||
| - | |sinopsis=Determinación del ángulo conocida una de sus razones empleando el circulo goniométrico. | ||
| - | }} | ||
| - | ---- | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 1 | ||
| - | |duracion=5´48" | ||
| - | |url1=https://www.youtube.com/watch?v=MbX11Sq8Gbo&index=8&list=PL8C0D37B1235315C7 | ||
| - | |sinopsis=Conocida una razón trigonométrica, hallar el ángulo: | ||
| - | |||
| - | En este vídeo empleamos la calculadora científica para determinar los dos ángulos del primer giro cuyo seno es 0.3 y los dos ángulos del primer giro cuyo seno es -0.4. | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 2 | ||
| - | |duracion=2´46" | ||
| - | |url1=https://www.youtube.com/watch?v=y98BqJEL2Ok&index=9&list=PL8C0D37B1235315C7 | ||
| - | |sinopsis=Conocida una razón trigonométrica, hallar el ángulo: | ||
| - | |||
| - | En este vídeo empleamos la calculadora científica para determinar los dos ángulos del primer giro cuyo coseno es 0.3 y los dos ángulos del primer giro cuyo coseno es -0.4. | ||
| - | }} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 3 | ||
| - | |duracion=3´52" | ||
| - | |url1=https://www.youtube.com/watch?v=9Q93GG7qRGo&index=10&list=PL8C0D37B1235315C7 | ||
| - | |sinopsis=Conocida una razón trigonométrica, hallar el ángulo. | ||
| - | |||
| - | En este vídeo empleamos la calculadora científica para determinar los dos ángulos del primer giro cuya tangente es 0.3 y los dos ángulos del primer giro cuya tangente es -0.8. | ||
| - | }} | ||
| - | }} | ||
| + | ==Funciones trigonométricas recíprocas== | ||
| + | {{Funciones trigonométricas recíprocas con calculadora}} | ||
| {{p}} | {{p}} | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 109)
Funciones trigonométricas
Estas funciones de la calculadora nos permiten obtener el las razones trigonométricas de un ángulo.
Seno
|
Calculadora: Seno |
Coseno
|
Calculadora: Coseno |
Tangente
|
Calculadora: Tangente |
En este vídeo aprendemos a emplear la calculadora científica para determinar las razones trigonométricas de un ángulo, ya esté expresado en el sistema sexagesimal o en el sistema circular.
Calcula usando la calculadora: 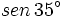
Calcula usando la calculadora: 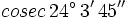
Calcula usando la calculadora: 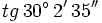
Calcula usando la calculadora: 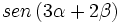 , siendo
, siendo 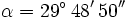 y
y 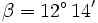 .
.
Calcula usando la calculadora: 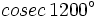 .
.
Calcula usando la calculadora: 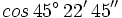 .
.
Calcula usando la calculadora: 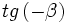 , siendo
, siendo 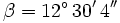 .
.
Calcula usando la calculadora: 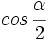 , siendo
, siendo 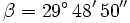 .
.
Calcula usando la calculadora: 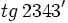 .
.
Calcula usando la calculadora: 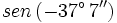 .
.
Calcula usando la calculadora: 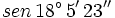 .
.
Calcula usando la calculadora: 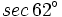 .
.
Funciones trigonométricas recíprocas
Estas funciones de la calculadora nos permiten obtener el ángulo a partir del valor de una razón trigonométrica.
Razones trigonométricas recíprocas. Ejemplos usando la calculadora.
Nota: En este vídeo las llama funciones trigonométricas inversas en vez de recíprocas.
Aco seno
|
Calculadora: Arco seno Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre -90º y 90º). Hay otra solución en el segundo o tercer cuadrante que se obtiene restando a 180º la solución obtenida. En este ejemplo, la otra solución sería 180º-30º=150º. |
Arco coseno
|
Calculadora: Arco coseno Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre 0º y 180º). Hay otra solución en el tercer o cuarto cuadrante que se obtiene restando a 360º la solución obtenida. En este ejemplo, la otra solución sería 360º-60º=300º. |
Arco tangente
|
Calculadora: Arco tangente Ejemplo:
Nota: La calculadora sólo da un valor del ángulo (el que se encuentra entre -90º y 90º). Hay otra solución en el segundo o tercer cuadrante que se obtiene sumando 180º a la solución obtenida. En este ejemplo, la otra solución sería 180º+45º=225º. |
|
Calculadora: Pasar ángulos con formato decimal a formato "grados, minutos y segundos" y viceversa |
|
Actividad: Trigonometría con calculadora Directas:
Inversas:
Recíprocas:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio resuelto: Trigonometría con calculadora
1. Calcula 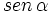 y
y 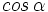 con la calculadora, sabiendo que
con la calculadora, sabiendo que 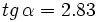 y que
y que 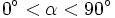
Primero se halla en ángulo:
Con ese valor se calcula:
En esta escena podrás ver como a partir del valor de una razón trigonométrica existen dos ángulos menores de 360º que tienen dicho valor.
Caso de ángulos agudos:
Dada una de las seis razones trigonométricas de un ángulo usa la calculadora científica para determinar el ángulo en el sistema sexagesimal (sólo calcula uno de los dos ángulos posibles):
Caso de ángulos cualesquiera:
Determinación del ángulo conocida una de sus razones empleando el circulo goniométrico.
Usa la calculadora científica para hallar los ángulos a partir de la razón trigonométrica dada:
- Determina los dos ángulos del primer giro cuyo seno es 0.3.
- Determina los dos ángulos del primer giro cuyo seno es -0.4.
Usa la calculadora científica para hallar los ángulos a partir de la razón trigonométrica dada:
- Determina los dos ángulos del primer giro cuyo coseno es 0.3.
- Determina los dos ángulos del primer giro cuyo coseno es -0.4.
Usa la calculadora científica para hallar los ángulos a partir de la razón trigonométrica dada:
- Determina los dos ángulos del primer giro cuya tangente es 0.3.
- Determina los dos ángulos del primer giro cuya tangente es -0.8.
Uso de las funciones trigonométricas recíprocas para la determinación del ángulo.
Uso de las funciones trigonométricas recíprocas para la determinación del ángulo.
Aviso: La notación usada en esta actividad no es la habitual. (Por ejemplo, normalmente se usa la expresión arcsen en vez de sen-1).
Ejercicios propuestos
|
Ejercicios propuestos: Trigonometría con calculadora |
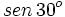
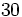
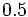
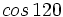
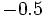
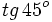
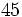
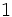
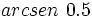
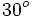 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).
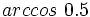
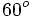 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).
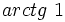
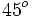 . Si la calculadora está en modo DEG (grados sexagesimales).
. Si la calculadora está en modo DEG (grados sexagesimales).