Biblioteca de plantillas
De Wikipedia
| Revisión de 15:31 19 sep 2007 Coordinador (Discusión | contribuciones) (→Desplegable) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Referencia histórica) |
||
| Línea 1: | Línea 1: | ||
| - | ==Iframes== | ||
| - | <center><iframe> | ||
| - | url=http://herramientas.educa.madrid.org/wiris/ | ||
| - | width=50% | ||
| - | height=400 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |||
| ==Menús== | ==Menús== | ||
| ===Menú Desplegable=== | ===Menú Desplegable=== | ||
| Línea 103: | Línea 95: | ||
| | 3|| 4,5 | | 3|| 4,5 | ||
| |} | |} | ||
| + | |||
| + | ===Tablabonitablanca=== | ||
| + | {|{{tablabonitablanca}} | ||
| + | |||
| + | ! Peso (kg) !! Precio (€) | ||
| + | |-align=center | ||
| + | |''' 1'''||1,5 | ||
| + | |-align=center | ||
| + | | 2|| 3 | ||
| + | |-align=center | ||
| + | | 3|| 4,5 | ||
| + | |} | ||
| + | |||
| ===Tabla75=== | ===Tabla75=== | ||
| {{Tabla75|celda1=1|celda2=2}} | {{Tabla75|celda1=1|celda2=2}} | ||
| ===Tabla50=== | ===Tabla50=== | ||
| {{Tabla50|celda1=1|celda2=2}} | {{Tabla50|celda1=1|celda2=2}} | ||
| + | ===Tabla25=== | ||
| + | {{Tabla25|celda1=1|celda2=2}} | ||
| + | |||
| + | ===Tabla3=== | ||
| + | {{Tabla3|celda1=1|celda2=2|celda3=3}} | ||
| + | ===Tabla3b=== | ||
| + | {{Tabla3b|celda1=1|celda2=2|celda3=3}} | ||
| + | |||
| + | ===Tabla4=== | ||
| + | {{Tabla4|celda1=1|celda2=2|celda3=3|celda4=4}} | ||
| ==Wiris== | ==Wiris== | ||
| Línea 114: | Línea 129: | ||
| |direccion=http://herramientas.educa.madrid.org/wiris/ | |direccion=http://herramientas.educa.madrid.org/wiris/ | ||
| }} | }} | ||
| + | |||
| + | ==Wolfram== | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Opuesto de un número entero'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | a) Calcula el opuesto de 3 | ||
| + | |||
| + | b) Calcula el opuesto de -5 | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | a) {{consulta|texto=opposite 3}} | ||
| + | |||
| + | b) {{consulta|texto=opposite -5}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ==Video== | ||
| + | ===Video enlace=== | ||
| + | {{Video_enlace | ||
| + | |titulo1=Matemáticas y realidad | ||
| + | |duracion=11´ | ||
| + | |url1=http://maralboran.org/web_ma/videos/realidad/realidad.htm | ||
| + | |titulo2=Acceso por red TIC | ||
| + | |url2=http://c0/helvia/aula/archivos/repositorio//0/117/html/index.htm | ||
| + | |sinopsis=La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Video enlace 2=== | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Matemáticas y realidad | ||
| + | |duracion=11´ | ||
| + | |url1=http://maralboran.org/web_ma/videos/realidad/realidad.htm | ||
| + | |sinopsis=La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Video enlace unicoos=== | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=0. Ejemplos | ||
| + | |duracion=8'45" | ||
| + | |sinopsis=:5 ejemplos. | ||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/funciones/caracteristicas-basicas/dominio-de-una-funcion | ||
| + | }} | ||
| + | ===Video enlace carreon=== | ||
| + | {{p}} | ||
| + | {{Video_enlace_carreon | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=5´15" | ||
| + | |sinopsis=Sucesiones con figuras | ||
| + | |url1=https://www.youtube.com/watch?v=SPJwfXwwaOg}} | ||
| + | |||
| + | {{p}} | ||
| + | |||
| + | ===Video enlace julioprofe=== | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo: Polinomios | ||
| + | |duracion=2'55" | ||
| + | |sinopsis=:Suma de polinomios. | ||
| + | |url1=https://www.youtube.com/watch?v=zRlJgiDVcPo}} | ||
| + | |||
| + | ===Video enlace fonemato=== | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Suma de números complejos | ||
| + | |duracion=8´53" | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/04-suma-de-numeros-complejos#.VCrucRa7ZV8 | ||
| + | |sinopsis=*Definición de suma de números complejos en forma binómica. | ||
| + | *Representación gráfica. | ||
| + | *Ejemplos. | ||
| + | *Propiedades. | ||
| + | }} | ||
| + | |||
| + | ===Videotutoriales=== | ||
| + | {{Videotutoriales | ||
| + | |titulo=Videotutoriales: Operaciones con complejos en forma binómica | ||
| + | |enunciado= | ||
| + | |||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Suma de números complejos | ||
| + | |duracion=8´53" | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/04-suma-de-numeros-complejos#.VCrucRa7ZV8 | ||
| + | |sinopsis=*Definición de suma de números complejos en forma binómica. | ||
| + | *Representación gráfica. | ||
| + | *Ejemplos. | ||
| + | *Propiedades. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Producto de números complejos | ||
| + | |duracion=11´26" | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/05-producto-de-numeros-complejos#.VCrvwha7ZV8 | ||
| + | |sinopsis=*Definición de producto de números complejos en forma binómica. | ||
| + | *Ejemplos. | ||
| + | *Propiedades. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Cociente de números complejos | ||
| + | |duracion=7´45" | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/06-cociente-de-numeros-complejos#.VCrw-Ba7ZV8 | ||
| + | |sinopsis= | ||
| + | *Definición de cociente de números complejos en forma binómica. | ||
| + | *Ejemplos. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1= Potenciación de números complejos expresados en forma binómica | ||
| + | |duracion=3´50" | ||
| + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/10-potenciacion-de-numeros-complejos-expresados-en-forma-binomica#.VCr30xa7ZV8 | ||
| + | |sinopsis=Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en [[Números complejos: Operaciones en forma polar (1ºBach)#Potencias de números complejos en forma polar|forma polar]] como se verá en otro apartado de este tema. | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| + | ===Video1=== | ||
| + | {{Video | ||
| + | |titulo=Pitágoras: mucho más que un teorema | ||
| + | |duracion=25´ | ||
| + | |sinopsis=Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema... | ||
| + | |video= | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm | ||
| + | width=100% | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | <center>[ '''Click''' aquí para enlace desde servidor TIC]</center> | ||
| + | }} | ||
| + | |||
| + | ===Video2=== | ||
| + | {{Video2 | ||
| + | |titulo1=Pitágoras: mucho más que un teorema | ||
| + | |titulo2=(Enlace por red TIC) | ||
| + | |duracion=25´ | ||
| + | |sinopsis=Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema... | ||
| + | |url1=http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm | ||
| + | |url2=http://c0/helvia/aula/archivos/repositorio//0/97/html/index.htm | ||
| + | }} | ||
| + | ===Video2b=== | ||
| + | {{Video2b | ||
| + | |titulo1=Pitágoras: mucho más que un teorema | ||
| + | |duracion=25´ | ||
| + | |sinopsis=Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema... | ||
| + | |url1=http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm | ||
| + | }} | ||
| + | |||
| + | ==Web== | ||
| + | {{Web_enlace | ||
| + | |descripcion=A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz. | ||
| + | |enlace=[http://w3.cnice.mec.es/eos/MaterialesEducativos/secundaria/matematicas/phi/index.htm Phi, el número de oro] | ||
| + | }} | ||
| + | {{Web | ||
| + | |titulo=Phi el número de oro | ||
| + | |descripcion=Web de Luis Nicolás Ortiz. | ||
| + | |enlace=http://w3.cnice.mec.es/eos/MaterialesEducativos/secundaria/matematicas/phi/index.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Web2 | ||
| + | |titulo=Phi el número de oro | ||
| + | |descripcion=Web de Luis Nicolás Ortiz. | ||
| + | |pagina= | ||
| + | <center><iframe> | ||
| + | url=http://w3.cnice.mec.es/eos/MaterialesEducativos/secundaria/matematicas/phi/index.htm | ||
| + | width=100% | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://w3.cnice.mec.es/eos/MaterialesEducativos/secundaria/matematicas/phi/index.htm '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | |||
| + | ==Geogebra== | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://ggbm.at/mfj4NVXn | ||
| + | width=100% | ||
| + | height=800 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |enlace=[https://ggbm.at/mfj4NVXn Razones trigonométricas de un ángulo cualquiera] | ||
| + | }} | ||
| + | |||
| + | ==MP3== | ||
| + | {{MP3 | ||
| + | |titulo1=Vonda Sheppard | ||
| + | |titulo2=I Only Wanna Be With You | ||
| + | |duracion=25´ | ||
| + | |comentario=Esta es una canción de ... | ||
| + | |reproductor=<mp3>http://maralboran.org/web_ma/vonda.mp3|download</mp3> | ||
| + | }} | ||
| + | |||
| + | |||
| ==Calculadora== | ==Calculadora== | ||
| {{Calculadora | {{Calculadora | ||
| Línea 124: | Línea 339: | ||
| |solucion= | |solucion= | ||
| <math>2.5219 \cdot 10^{-03}</math>}} | <math>2.5219 \cdot 10^{-03}</math>}} | ||
| + | {{p}} | ||
| + | ===Calculadora2=== | ||
| + | {|width=100% | ||
| + | |style="background: white; border:2px solid DarkSlateBlue;border-left:4px solid DarkSlateBlue;border-bottom:4px solid DarkSlateBlue; padding:.75em;"|[[Image:Fx100ms.jpg|30px|left|Calculadora]] | ||
| + | <font color="Indigo">'''{{{titulo}}}'''</font> | ||
| + | ---- | ||
| + | {{p}} | ||
| + | {{{cuerpo}}} | ||
| + | |} | ||
| - | ==Teorema== | + | ==Teoremas== |
| + | ===Teorema=== | ||
| {{Teorema|titulo=Teorema de Pitágoras|enunciado=En un trian...|demo=esta es la demo}} | {{Teorema|titulo=Teorema de Pitágoras|enunciado=En un trian...|demo=esta es la demo}} | ||
| + | {{p}} | ||
| + | ===Teorema sin demo=== | ||
| + | {{Teorema_sin_demo|titulo=Teorema de Pitágoras|enunciado=En un trian...}} | ||
| - | ==Ejemplo== | + | ==Ejemplos== |
| + | ===Ejemplo_simple (sin caja)=== | ||
| + | {{Ejemplo_simple|titulo=Ejemplo | ||
| + | |contenido= | ||
| + | *12 es múltiplo de 4 <math>(12= \dot 4)</math> porque <math>12=4 \cdot 3</math>. Por tanto, 4 es divisor de 12 <math>(4|12 \;\!)</math>. | ||
| + | }} | ||
| + | |||
| + | ===Ejemplo (con solución)=== | ||
| {{Ejemplo | {{Ejemplo | ||
| |titulo=Ejemplo 1: ''Tema'' | |titulo=Ejemplo 1: ''Tema'' | ||
| Línea 135: | Línea 370: | ||
| |sol= | |sol= | ||
| Esta es la sol}} | Esta es la sol}} | ||
| + | |||
| + | ===Ejemplo2 (sin solución)=== | ||
| + | {{Ejemplo2 | ||
| + | |titulo=Ejemplo 1: ''Tema'' | ||
| + | |enunciado= | ||
| + | Este es el ejemplo.}} | ||
| + | |||
| + | ===Ejemplos múltiples=== | ||
| + | {{p}} | ||
| + | {{ejemplo2 | ||
| + | |titulo=Ejemplos: ''Ecuaciones trigonométricas'' | ||
| + | |enunciado= | ||
| + | |||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | '''1. '''Resuelve: <math>2 \, tg \, x - 3\, cot \, x - 1=0</math> | ||
| + | |sol= | ||
| + | Transformamos la ecuación de partida: | ||
| + | |||
| + | :<math>2 \, tg \, x - \cfrac{3}{tg \, x} - 1=0</math> | ||
| + | :<math>2 \, tg^2 \, x - tg \, x - 3=0</math> | ||
| + | |||
| + | Hacemos un cambio de variable: <math>z= tg \, x</math> | ||
| + | |||
| + | :<math>2z^2- z - 3=0 \,</math> | ||
| + | :<math>z=\cfrac{1 \pm \sqrt{1+24}}{4}=\cfrac{1 \pm 5}{4}= | ||
| + | \begin{cases} z_1=\cfrac{3}{2}\\ z_2=-1 \end{cases} | ||
| + | </math> | ||
| + | |||
| + | :<math>\begin{cases} z_1=\cfrac{3}{2} \rightarrow tg \, x_1=\cfrac{3}{2} \rightarrow x_1 = arctg \, \cfrac{3}{2}=56^\circ \, 18' \, 35'' + 180^\circ \cdot k\\ z_2=-1 \rightarrow tg \, x_2=-1 \rightarrow x_2 = arctg \, -1=135^\circ + 180^\circ \cdot k \end{cases} \, , \quad k \in \mathbb{Z}</math> | ||
| + | |||
| + | '''Soluciones:''' | ||
| + | |||
| + | :<math>\begin{cases} x_1 =56^\circ \, 18' \, 35'' + 180^\circ \cdot k\\x_2=135^\circ + 180^\circ \cdot k\end{cases} \, , \quad k \in \mathbb{Z}</math> | ||
| + | }} | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | '''2. '''Resuelve: {{sube|porcentaje=+20%|contenido=<math>cos^2 \, x - 3\, sen^2 \, x =0</math>}} | ||
| + | |sol= | ||
| + | Usando la identidad fundamental: | ||
| + | |||
| + | :<math>sen^2 \, x + cos^2 \, x = 1 \rightarrow cos^2 \, x = 1 - sen^2 \, x</math> | ||
| + | |||
| + | Sustituimos en nuestra ecuación de partida: | ||
| + | |||
| + | :<math>1-sen^2 \, x - 3\, sen^2 \, x =0</math> | ||
| + | :<math>1-4 \, sen^2 \, x =0 \rightarrow sen^2 \, x =\cfrac{1}{4}\rightarrow sen \, x =\pm \cfrac{1}{2}</math> | ||
| + | |||
| + | '''Soluciones:''' | ||
| + | |||
| + | :<math>x=\begin{cases} arcsen \, \cfrac{1}{2}= | ||
| + | \begin{cases} | ||
| + | x_1 =30^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_2 =150^\circ + 360^\circ \cdot k | ||
| + | |||
| + | \end{cases} | ||
| + | |||
| + | |||
| + | \\ | ||
| + | arcsen \, -\cfrac{1}{2}= | ||
| + | \begin{cases} | ||
| + | x_3 =210^\circ + 360^\circ \cdot k | ||
| + | \\ | ||
| + | x_4 =330^\circ + 360^\circ \cdot k | ||
| + | |||
| + | \end{cases} | ||
| + | x_2=135^\circ + 180^\circ \cdot k \end{cases} \, , \quad k \in \mathbb{Z}</math> | ||
| + | |||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| + | ==Compositores== | ||
| + | {{Compositores | ||
| + | |Compositor=Joaquín Rodrigo | ||
| + | |Obra=Concierto de Aranjuez | ||
| + | |||
| + | |Esquema= | ||
| + | Aquí viene el esquema}} | ||
| ==Ejercicios== | ==Ejercicios== | ||
| Línea 146: | Línea 461: | ||
| #¿Qué diferencia hay entre realizar un muestro probabilístico o no probabilístico? | #¿Qué diferencia hay entre realizar un muestro probabilístico o no probabilístico? | ||
| }} | }} | ||
| + | |||
| + | ===Wolfram=== | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Valor numérico de una expresión algebraica'' | ||
| + | |cuerpo= | ||
| + | Calcula el valor numérico del polinomio <math>a^2-2ax+4\;\!</math> en los casos: | ||
| + | ---- | ||
| + | {{Tabla75 | ||
| + | |celda1='''1)''' <math>a=2 \, , \ x=3\;\!</math> | ||
| + | |celda2= | ||
| + | [http://www.wolframalpha.com/input/?i=a%5E2-2ax%2B4+where+a%3D0%2C+x%3D0 Solución] | ||
| + | }} | ||
| + | ---- | ||
| + | {{Tabla75 | ||
| + | |celda1='''2)''' <math>a=-2 \, , \ x=1\;\!</math> | ||
| + | |celda2= | ||
| + | [http://www.wolframalpha.com/input/?i=a%5E2-2ax%2B4+where+a%3D0%-2C+x%1D0 Solución] | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Wolfram con widget=== | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Operaciones aritméticas'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | '''1. '''Calcula: | ||
| + | |||
| + | :a) <math>9+4\cdot7-2=</math> | ||
| + | |||
| + | :b) <math>(9+4)\cdot7-2=</math> | ||
| + | |||
| + | :c) <math>9+4\cdot(7-2)=</math> | ||
| + | |||
| + | :d) <math>(9+4)\cdot(7-2)=</math> | ||
| + | <br> | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) 9+4*7-2 | ||
| + | :b) (9+4)*(7-2) | ||
| + | :c) 9+4*(7-2) | ||
| + | :d) (9+4)*(7-2) | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/wikipedia/extensions/wolfram.php | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | ===Wolfram desplegable=== | ||
| + | {{wolfram_desplegable|titulo=Título|contenido=}} | ||
| ===Ejercicios (con solución)=== | ===Ejercicios (con solución)=== | ||
| Línea 183: | Línea 553: | ||
| ===Caja Amarilla=== | ===Caja Amarilla=== | ||
| {{Caja Amarilla|texto=Este es el contenido}}<br> | {{Caja Amarilla|texto=Este es el contenido}}<br> | ||
| + | |||
| + | ===Caja Naranjaa=== | ||
| + | {{Caja Naranja|texto=Este es el contenido}}<br> | ||
| ===Caja=== | ===Caja=== | ||
| Línea 190: | Línea 563: | ||
| ==Actividad interactiva== | ==Actividad interactiva== | ||
| + | ===Actividades=== | ||
| + | {{Actividades|titulo=|enunciado=}} | ||
| + | ===AI enlace=== | ||
| + | {{AI_enlace | ||
| + | |titulo1=El papiro Rhind | ||
| + | |descripcion=Un poco de historia sobre el papiro de Rhind. Las fracciones unitarias. | ||
| + | |url1=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411251251_PRE_0_1393288747&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0 | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Números naturales | ||
| + | |descripcion=El sistema de numeración decimal permite escribir cualquier número con diez símbolos: | ||
| + | |||
| + | 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 | ||
| + | |||
| + | Estos diez símbolos se llaman cifras o dígitos. | ||
| + | |||
| + | En un número, el valor de cada cifra depende de la posición que ocupa: unidades, decenas, centenas, unidades de mil o de millar, decenas de millar... | ||
| + | |||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena1/1quincena1_contenidos_1a.htm | ||
| + | }} | ||
| + | |||
| ===AI=== | ===AI=== | ||
| {{AI|titulo=Actividades Interactivas (Potencias)|enunciado= | {{AI|titulo=Actividades Interactivas (Potencias)|enunciado= | ||
| Línea 216: | Línea 610: | ||
| }} | }} | ||
| }} | }} | ||
| - | ==Desplegable== | + | ===AI3=== |
| + | {{AI3|titulo=Formas de expresar una función | ||
| + | |enunciado=Caso de variable discreta. | ||
| + | |actividad= | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Interpretacion_de_graficas/Graficas_1.html | ||
| + | width=50% | ||
| + | height=adjust | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | |||
| + | ==Desplegables== | ||
| + | ===Desplegable=== | ||
| + | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| + | Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Radicales/radicales1_2.html | ||
| + | width=500 | ||
| + | height=230 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | {{p}} | ||
| {{Desplegable | {{Desplegable | ||
| |titulo=<font color="#0000FF">Números:</font> <font color="#000000"></font> | |titulo=<font color="#0000FF">Números:</font> <font color="#000000"></font> | ||
| Línea 229: | Línea 647: | ||
| *[http://maralboran.ath.cx/web_ma/ejercicios/2eso/Proporcionalidad.doc Regla de Tres] | *[http://maralboran.ath.cx/web_ma/ejercicios/2eso/Proporcionalidad.doc Regla de Tres] | ||
| }} | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | ===Desplegable2=== |
| - | + | {{Desplegable2 | |
| - | Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno: | + | |titulo=Demostración: |
| + | |contenido=Sea AB un diámetro de la circunferencia: <math>\widehat{AOB}=180^o</math>. Por el apartado a), el ángulo inscrito <math>\widehat{AVB}=\cfrac{180^o}{2}=90^o</math>. | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Radicales/radicales1_2.html | + | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_4.html |
| - | width=500 | + | width=420 |
| - | height=230 | + | height=350 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | Mueve el vértice V y comprueba que el ángulo siempre es recto. Este resultado proporciona una excelente forma de construir ángulos rectos y triángulos rectángulos. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===Advertencia=== | ||
| + | {{Warning|titulo=Advertencia:|texto= | ||
| + | Puesto que los números naturales se utilizan para contar elementos, el '''cero''' (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Nota=== | ||
| + | {{Nota|titulo=Notación:|texto= | ||
| + | Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes: | ||
| + | {{p}} | ||
| + | *Menor o igual que (<math>\le\;</math>) | ||
| + | *Mayor o igual que (<math>\ge\;</math>) | ||
| + | *Distinto (<math>\ne\;</math>) | ||
| + | }} | ||
| + | |||
| + | ===Historia=== | ||
| + | {{Historia|titulo=El formarto DIN A:|texto= | ||
| + | [[Imagen:dina4.jpg|thumb|300px|[http://blog.imprentaonline24.es/tamano-de-papel/ ''blog.imprentaonline24.es'']]] | ||
| + | No es necesario estar vinculado al sector de las Artes Gráficas o al mundo del diseño para estar en contacto diario con el sistema de clasificación o medidas de papel DIN A. Seguramente si alguna vez habrás tenido que imprimir un documento o imagen en un tamaño en concreto. Y en algún momento nos hemos preguntado si nuestra impresora podría tolerar ese tamaño de impresión. Estamos habituados a escuchar que si tal o cual formato está en A4, A3, A5, etc. ¿pero de qué manera funcionan todos? ¿cuál es su origen y sus utilidades? A continuación respondemos a estas preguntas. | ||
| + | |||
| + | DIN no es más que un acrónimo que significa Deutches Institut für Normung, que traducido significa Instituto Alemán de Normalización. Esta entidad que surgió en 1917 es la encargada de dictar los estándares o normas técnicas en Alemania. Dichas normas tienen como finalidad exclusiva asegurar y garantizar la calidad de aquello que se quiere normalizar, en este caso el tamaño del papel. Aunque quizás pienses que la normativa DIN sólo hace referencia al formato del papel, lo cierto es que existen y puedes encontrar aproximadamente 30.000 normativas DIN en este 2016 según archivo. | ||
| + | |||
| + | Fue el ingeniero berlinés Walter Porstmann quien estableció hacia el año 1922 las medidas DIN A a partir de la incorporación de la normativa [http://es.wikipedia.org/wiki/DIN_476 DIN 476]. El propósito era estandarizar de alguna manera los diferentes [http://es.wikipedia.org/wiki/Formato_de_papel formatos de papel] o página para aprovechar el máximo de papel y que hubiera el mínimo desperdicio posible. Dentro de la misma normativa DIN 476 encontramos la serie A, donde se definen precisamente estas medidas. Junto a la serie A también existen otras cuatro plantillas B, C, D y E y cada una de ellas contiene una numeración de varios tamaños: 0, 1, 2, 3, 4, 5, etc. | ||
| + | |||
| + | Las medidas DIN A parten de un formato referente que es el A0. El resto de formatos y series se calculan siempre a partir de éste. | ||
| + | |||
| + | En la serie A, al tamaño de papel de 1 m<sup>2</sup> se le llama A0. Las divisiones posteriores que disminuyen la superficie a la mitad, reciben el nombre de A1, A2, A3, A4, etc. Lo que en realidad está indicando la numeración asociada a la letra A es la cantidad de cortes a la mitad desde la hoja original. Así por ejemplo, una hoja tamaño A4 tiene una superficie igual a la mitad de una hoja medida A3. | ||
| + | |||
| + | Cuando se corta por la mitad una hoja en tamaño A0 (1 m<sup>2</sup>), el lado más corto se convierte en la parte más larga de la hoja resultante (A1). Por tanto, si cortamos cualquier hoja de la serie a la mitad de su lado más largo, obtendremos siempre dos hojas del tamaño siguiente, que al mismo tiempo mantienen perfectamente las proporciones entre el ancho y el largo, siendo la razón de proporcionalidad igual a la raíz cuadrada de 2. Es decir, para cualquier formato DIN A, si dividimos el largo entre el ancho, nos dará (aproximadamente) 1,4142. | ||
| + | |||
| + | Puedes hacer la prueba: Mide el ancho y largo de una hoja tamaño DIN A4 y verás que se cumple la proporción; dóblala por el lado más largo y pártela por la mitad, mide el ancho y el largo de una de las mitades, divide las dos cifras y verás que se sigue cumpliendo: 1,4142. | ||
| + | |||
| + | Veamos la demostración: | ||
| + | |||
| + | [[Imagen:FormatoDIN.png|300px|right]] | ||
| + | |||
| + | Partiendo de un formato de lados '''a''' y '''b''', el formato superior tendrá '''2a''' por '''b''', para que la proporción entre sus lados sea la misma tendrá que cumplirse que: | ||
| + | : <math> | ||
| + | \cfrac{b}{a} = \cfrac{2a}{b} | ||
| + | </math> | ||
| + | |||
| + | Esto es: | ||
| + | : <math> | ||
| + | \cfrac{b^2}{a^2} = 2 \rightarrow \quad | ||
| + | \left ( | ||
| + | {\cfrac{b}{a}} | ||
| + | \right ) | ||
| + | ^2 = 2 \rightarrow \quad | ||
| + | \cfrac{b}{a} =\sqrt{2} \rightarrow \quad | ||
| + | b = \sqrt{2} \cdot a | ||
| + | </math> | ||
| + | |||
| + | Si la proporción entre el lado mayor y menor es raíz de dos, cortando un formato en dos iguales esta proporción se conserva. | ||
| + | |||
| + | Si el formato '''A0''' tiene una superficie de un metro cuadrado, tendremos: | ||
| + | : <math> | ||
| + | \left . | ||
| + | \begin{matrix} | ||
| + | a \cdot b = 1m^2 \\ | ||
| + | \\ | ||
| + | b = \sqrt{2} \cdot a | ||
| + | \end{matrix} | ||
| + | \right \} | ||
| + | \rightarrow \quad | ||
| + | a \cdot (\sqrt{2} \cdot a) = 1m^2 | ||
| + | \rightarrow \quad | ||
| + | \sqrt{2} \cdot a^2 = 1m^2 | ||
| + | \rightarrow | ||
| + | </math> | ||
| + | : <math> | ||
| + | a^2 = \cfrac{1m^2}{\sqrt{2}} | ||
| + | \rightarrow \quad | ||
| + | a = \sqrt{\cfrac{1m^2}{\sqrt{2}}} | ||
| + | = \cfrac{1m}{\sqrt[4]{2}} | ||
| + | = \cfrac{1}{1,189} \; m | ||
| + | = 0,841 \; m | ||
| + | </math> | ||
| + | |||
| + | Sabiendo el valor de '''a''' el cálculo de '''b''' es inmediato: | ||
| + | : <math> | ||
| + | \left . | ||
| + | \begin{matrix} | ||
| + | a \cdot b = 1 m^2 \\ | ||
| + | \\ | ||
| + | a = 0,841 m | ||
| + | \end{matrix} | ||
| + | \right \} | ||
| + | \rightarrow \quad | ||
| + | (0,841 m) \cdot b = 1 m^2 | ||
| + | \rightarrow \quad | ||
| + | b = \cfrac{1 m^2}{0,841 m} | ||
| + | = 1,189 m | ||
| + | </math> | ||
| + | |||
| + | Lo que podemos resumir como regla mnemotécnica que el formato '''DIN A0''', tiene por medidas: | ||
| + | : <math> | ||
| + | DIN \; A0 \quad | ||
| + | \left \{ | ||
| + | \begin{matrix} | ||
| + | ancho = \cfrac{1}{\sqrt[4]{2}} \; m \\ | ||
| + | \\ | ||
| + | largo = \sqrt[4]{2} \; m | ||
| + | \end{matrix} | ||
| + | \right . | ||
| + | </math> | ||
| + | |||
| + | Dividiendo el lado mayor entre dos, obtendremos sucesivamente los distintos formatos '''A1''', '''A2''', '''A3''', '''A4''' ... | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Información== | ||
| + | {{p}} | ||
| + | {{Info|texto=Para más información: [[Números naturales]]}} | ||
| + | {{p}} | ||
| + | ==Tarea== | ||
| + | {{Tarea | ||
| + | |fecha=09/11/07 | ||
| + | |asignatura=Matemáticas | ||
| + | |blink=on | ||
| + | |contenido=Libro: Ejercicios 1 al 9 (pág. 61) | ||
| + | }} | ||
| + | |||
| + | ==Eventos calendario== | ||
| + | '''Sintaxis:''' | ||
| + | <pre><nowiki> | ||
| + | {{Evento | ||
| + | |tipo=Puede ser uno de los 4 siguientes: Tarea, Examen, Act.Extraescolar, Otros | ||
| + | |asignatura=Asignatura | ||
| + | |contenido=Explicación del evento | ||
| + | }}</nowiki></pre> | ||
| + | |||
| + | '''Ejemplos''' | ||
| + | *'''tipo=Tarea''' {{Evento | ||
| + | |tipo=Tarea | ||
| + | |asignatura=Matemáticas | ||
| + | |contenido=Libro: Ejercicios 1 al 9 (pág. 61) | ||
| + | }} | ||
| + | *'''tipo=Examen''' {{Evento | ||
| + | |tipo=Examen | ||
| + | |asignatura=Lengua | ||
| + | |contenido=Libro: Tema 2 | ||
| + | }} | ||
| + | *'''tipo=Act.Extraescolar''' {{Evento | ||
| + | |tipo=Act.Extraescolar | ||
| + | |asignatura=Física y Química | ||
| + | |contenido=Visita al Parque de las Ciencias en Granada | ||
| + | }} | ||
| + | *'''tipo=Otros''' {{Evento | ||
| + | |tipo=Otros | ||
| + | |asignatura=Tutoría | ||
| + | |contenido=Entrega de notas | ||
| + | }} | ||
Revisión actual
Tabla de contenidos |
Menús
Menú Desplegable
| Ir a | Para repasar | Para ampliar | Herramientas |
| Indice | Tablas multiplicar | Números naturales | WIRIS |
Menú Derecha
| NUMEROS NATURALES |
| Ir a |
| Para ampliar |
| Para repasar |
| Herramientas |
Menú Asignatura
| Enlaces |
| Descartes WIRIS Geometría (E.S.O.) |
| Ejercicios |
| E.S.O. Bachillerato |
| Multimedia |
| {{{multimedia}}} |
| Documentos |
| Exámenes Programaciones |
Tablas
Tablabonita
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tablabonitablanca
| Peso (kg) | Precio (€) |
|---|---|
| 1 | 1,5 |
| 2 | 3 |
| 3 | 4,5 |
Tabla75
| 1 | 2 |
Tabla50
| 1 | 2 |
Tabla25
| 1 | 2 |
Tabla3
| 1 | 2 | 3 |
Tabla3b
| 1 | 2 | 3 |
Tabla4
| 1 | 2 | 3 | 4 |
Wiris
Wolfram
|
Actividad: Opuesto de un número entero a) Calcula el opuesto de 3 b) Calcula el opuesto de -5 Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) opposite 3 b) opposite -5 |
Video
Video enlace
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video enlace 2
La belleza de las formas geométricas en la Alhambra de Granada es incuestionable; pero un grupo de alumnos de la Escuela de Arquitectura nos sorprenderá dando a algunas de las figuras geométricas nazaríes una aplicación práctica y funcional, como el diseño de una escuela o una urbanización de chalets. Veremos además cómo las matemáticas ayudan a medir y cuantificar fenómenos naturales tan distintos como la intensidad de un terremoto, el brillo de las estrellas o el ruido de nuestras calles.
Video enlace unicoos
- 5 ejemplos.
Video enlace carreon
Sucesiones con figuras
Video enlace julioprofe
- Suma de polinomios.
Video enlace fonemato
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
Videotutoriales
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
- Definición de producto de números complejos en forma binómica.
- Ejemplos.
- Propiedades.
- Definición de cociente de números complejos en forma binómica.
- Ejemplos.
Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en forma polar como se verá en otro apartado de este tema.
Video1
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Video2b
Video: Pitágoras: mucho más que un teorema (25´)
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema...
Web
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
Web: Phi el número de oro
Web de Luis Nicolás Ortiz.
Geogebra
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
MP3
Calculadora
|
Calculadora: Notación científica |
Calculadora2
|
{{{titulo}}} {{{cuerpo}}} |
Teoremas
Teorema
Teorema sin demo
Ejemplos
Ejemplo_simple (sin caja)
Ejemplo (con solución)
Ejemplo2 (sin solución)
Ejemplos múltiples
Ejemplos: Ecuaciones trigonométricas
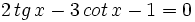
Transformamos la ecuación de partida:
Hacemos un cambio de variable: 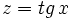
Soluciones:
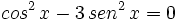
Usando la identidad fundamental:
Sustituimos en nuestra ecuación de partida:
Soluciones:
Compositores
Ejercicios
Actividad (sin solución)
|
Actividad 1
|
Wolfram
|
Actividad: Valor numérico de una expresión algebraica |
Wolfram con widget
|
Actividad: Operaciones aritméticas 1. Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Wolfram desplegable
Ejercicios (con solución)
|
Ejercicios 1. Calcula:
Solución: a) 35 b) 89 c) 29 d) 65
2. En una división, el dividendo es 969, el cociente 74, y el resto 7. ¿Cúal es el divisor?
Solución: El divisor es 13 |
Ecuación (con número de referencia)
| Aquí vendría la fórmula | (Num. Ref.) |
Cajas
Caja Amarilla
Este es el contenido
Caja Naranjaa
Este es el contenido
Caja
|
Aquí vendría la fórmula |
Actividad interactiva
Actividades
AI enlace
Un poco de historia sobre el papiro de Rhind. Las fracciones unitarias.
El sistema de numeración decimal permite escribir cualquier número con diez símbolos:
0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
Estos diez símbolos se llaman cifras o dígitos.
En un número, el valor de cada cifra depende de la posición que ocupa: unidades, decenas, centenas, unidades de mil o de millar, decenas de millar...
AI
AI2
|
Actividades Interactivas: Formas de expresar una función
1. Variable discreta.
Actividad:
2. Variable continua.
Actividad: El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas. |
AI3
Desplegables
Desplegable
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Desplegable2
Sea AB un diámetro de la circunferencia: 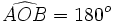 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 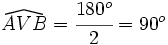 .
.
Advertencia
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Nota
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
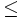 )
)
- Mayor o igual que (
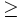 )
)
- Distinto (
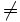 )
)
Historia
No es necesario estar vinculado al sector de las Artes Gráficas o al mundo del diseño para estar en contacto diario con el sistema de clasificación o medidas de papel DIN A. Seguramente si alguna vez habrás tenido que imprimir un documento o imagen en un tamaño en concreto. Y en algún momento nos hemos preguntado si nuestra impresora podría tolerar ese tamaño de impresión. Estamos habituados a escuchar que si tal o cual formato está en A4, A3, A5, etc. ¿pero de qué manera funcionan todos? ¿cuál es su origen y sus utilidades? A continuación respondemos a estas preguntas.
DIN no es más que un acrónimo que significa Deutches Institut für Normung, que traducido significa Instituto Alemán de Normalización. Esta entidad que surgió en 1917 es la encargada de dictar los estándares o normas técnicas en Alemania. Dichas normas tienen como finalidad exclusiva asegurar y garantizar la calidad de aquello que se quiere normalizar, en este caso el tamaño del papel. Aunque quizás pienses que la normativa DIN sólo hace referencia al formato del papel, lo cierto es que existen y puedes encontrar aproximadamente 30.000 normativas DIN en este 2016 según archivo.
Fue el ingeniero berlinés Walter Porstmann quien estableció hacia el año 1922 las medidas DIN A a partir de la incorporación de la normativa DIN 476. El propósito era estandarizar de alguna manera los diferentes formatos de papel o página para aprovechar el máximo de papel y que hubiera el mínimo desperdicio posible. Dentro de la misma normativa DIN 476 encontramos la serie A, donde se definen precisamente estas medidas. Junto a la serie A también existen otras cuatro plantillas B, C, D y E y cada una de ellas contiene una numeración de varios tamaños: 0, 1, 2, 3, 4, 5, etc.
Las medidas DIN A parten de un formato referente que es el A0. El resto de formatos y series se calculan siempre a partir de éste.
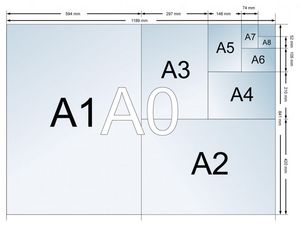
En la serie A, al tamaño de papel de 1 m2 se le llama A0. Las divisiones posteriores que disminuyen la superficie a la mitad, reciben el nombre de A1, A2, A3, A4, etc. Lo que en realidad está indicando la numeración asociada a la letra A es la cantidad de cortes a la mitad desde la hoja original. Así por ejemplo, una hoja tamaño A4 tiene una superficie igual a la mitad de una hoja medida A3.
Cuando se corta por la mitad una hoja en tamaño A0 (1 m2), el lado más corto se convierte en la parte más larga de la hoja resultante (A1). Por tanto, si cortamos cualquier hoja de la serie a la mitad de su lado más largo, obtendremos siempre dos hojas del tamaño siguiente, que al mismo tiempo mantienen perfectamente las proporciones entre el ancho y el largo, siendo la razón de proporcionalidad igual a la raíz cuadrada de 2. Es decir, para cualquier formato DIN A, si dividimos el largo entre el ancho, nos dará (aproximadamente) 1,4142.
Puedes hacer la prueba: Mide el ancho y largo de una hoja tamaño DIN A4 y verás que se cumple la proporción; dóblala por el lado más largo y pártela por la mitad, mide el ancho y el largo de una de las mitades, divide las dos cifras y verás que se sigue cumpliendo: 1,4142.
Veamos la demostración:
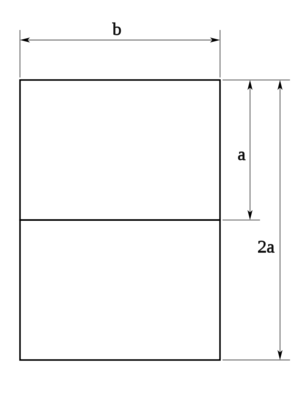
Partiendo de un formato de lados a y b, el formato superior tendrá 2a por b, para que la proporción entre sus lados sea la misma tendrá que cumplirse que:
Esto es:
Si la proporción entre el lado mayor y menor es raíz de dos, cortando un formato en dos iguales esta proporción se conserva.
Si el formato A0 tiene una superficie de un metro cuadrado, tendremos:
Sabiendo el valor de a el cálculo de b es inmediato:
Lo que podemos resumir como regla mnemotécnica que el formato DIN A0, tiene por medidas:
Dividiendo el lado mayor entre dos, obtendremos sucesivamente los distintos formatos A1, A2, A3, A4 ...
Información
Tarea
Eventos calendario
Sintaxis:
{{Evento
|tipo=Puede ser uno de los 4 siguientes: Tarea, Examen, Act.Extraescolar, Otros
|asignatura=Asignatura
|contenido=Explicación del evento
}}
Ejemplos

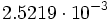

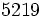

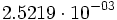
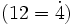 porque
porque 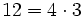 . Por tanto, 4 es divisor de 12
. Por tanto, 4 es divisor de 12 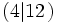 .
.
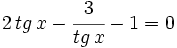
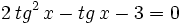
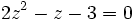
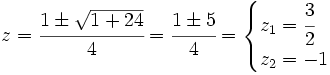
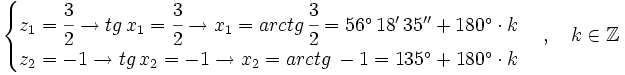
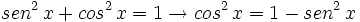
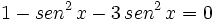
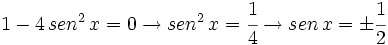
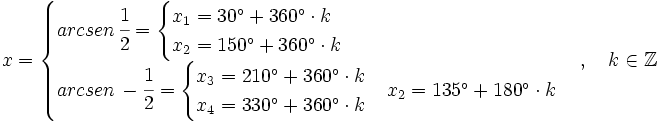
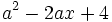 en los casos:
en los casos:
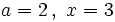
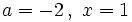
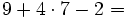
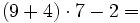
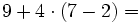
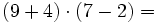
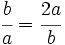
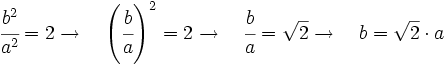
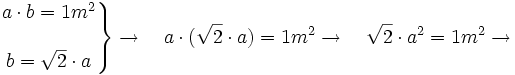
![a^2 = \cfrac{1m^2}{\sqrt{2}} \rightarrow \quad a = \sqrt{\cfrac{1m^2}{\sqrt{2}}} = \cfrac{1m}{\sqrt[4]{2}} = \cfrac{1}{1,189} \; m = 0,841 \; m](/wikipedia/images/math/e/d/6/ed67279193d5f651e1b3f739d1f96eb0.png)
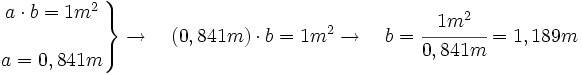
![DIN \; A0 \quad \left \{ \begin{matrix} ancho = \cfrac{1}{\sqrt[4]{2}} \; m \\ \\ largo = \sqrt[4]{2} \; m \end{matrix} \right .](/wikipedia/images/math/9/6/3/96380202caaa3fd258db9e669b1fa5c6.png)

