Plantilla:Raiz de 2 no es racional
De Wikipedia
| Revisión de 18:28 7 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 2: | Línea 2: | ||
| |titulo=Proposición | |titulo=Proposición | ||
| |enunciado= | |enunciado= | ||
| - | :No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número{{sube|porcentaje=+20%|contenido=<math>\sqrt{2} \,</math>}} no es racional. | + | No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número{{sube|porcentaje=+20%|contenido=<math>\sqrt{2} \,</math>}} no es racional. |
| |demo= | |demo= | ||
| + | '''Demostración:''' | ||
| + | {{p}} | ||
| Vamos ha utilizar un tipo de demostración denominado "[[Método de reducción al absurdo |por reducción al absurdo]]". Supondremos que{{sube|porcentaje=+20%|contenido=<math>\sqrt{2} \,</math>}} es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida. | Vamos ha utilizar un tipo de demostración denominado "[[Método de reducción al absurdo |por reducción al absurdo]]". Supondremos que{{sube|porcentaje=+20%|contenido=<math>\sqrt{2} \,</math>}} es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida. | ||
| Línea 20: | Línea 22: | ||
| Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces. | Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces. | ||
| - | Como {{sube|porcentaje=+25%|contenido=<math>b^2\;\!</math>}} es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Pero, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto {{sube|porcentaje=+25%|contenido=<math>a^2\;\!</math>}}, lo cual no es posible. | + | Como {{sube|porcentaje=+25%|contenido=<math>b^2\;\!</math>}} es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto {{sube|porcentaje=+25%|contenido=<math>a^2\;\!</math>}}, lo cual no es posible. |
| - | Ya hemos llegado al absurdo. | + | Ya hemos llegado al absurdo. |
| + | ---- | ||
| + | Tambián puedes ver la demostración en el siguiente videotutorial: | ||
| + | {{p}} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Demostración de la irracionalidad de la raíz de 2 | ||
| + | |duracion=11´57" | ||
| + | |sinopsis=Videotutorial con otra demostración de la irracionalidad de la raíz de 2. | ||
| + | |url1=https://www.youtube.com/watch?v=gGWlqg-13hk}} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Demostración con un poco de historia. | ||
| + | |duracion=4´09" | ||
| + | |sinopsis=Videotutorial con la misma demostración que el video e Khan, pero más rápida y con un poco de historia. | ||
| + | |url1=https://youtu.be/xeBJrWlMdoI}} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unpuntocircular | ||
| + | |titulo1=Un número secreto | ||
| + | |duracion=2´49" | ||
| + | |url1=https://www.youtube.com/watch?v=GJ7KNpAYIOg | ||
| + | |sinopsis=Una breve historia de un número cuyo cuadrado es 2. | ||
| + | }} | ||
| + | {{Video_enlace_derivando | ||
| + | |titulo1=El formato DIN A4 y la raíz de 2 | ||
| + | |duracion=4´40" | ||
| + | |url1=https://youtu.be/G1Zkiytd8vE | ||
| + | |sinopsis= | ||
| + | ¡La de matemáticas que hay en un folio! ¿Sabes de dónde proviene el formato de hojas A4?. | ||
| + | }} | ||
| + | {{Historia|titulo=El formarto DIN A:|texto= | ||
| + | {{El formato DIN A}} | ||
| + | }} | ||
| + | {{p}} | ||
Revisión actual
Proposición
No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número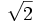 no es racional.
no es racional.
Demostración:
Vamos ha utilizar un tipo de demostración denominado "por reducción al absurdo". Supondremos que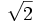 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que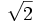 es racional, o sea, que existe una fracción que es igual a
es racional, o sea, que existe una fracción que es igual a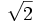 .
.
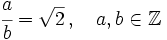
Elevamos al cuadrado los dos miembros de la igualdad:
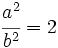
Multiplicamos por 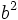 los dos miembros de la igualdad:
los dos miembros de la igualdad:
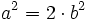 [1]
[1]Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces.
Como 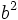 es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto
es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto 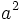 , lo cual no es posible.
, lo cual no es posible.
Ya hemos llegado al absurdo.
Tambián puedes ver la demostración en el siguiente videotutorial:
Videotutorial con otra demostración de la irracionalidad de la raíz de 2.
Videotutorial con la misma demostración que el video e Khan, pero más rápida y con un poco de historia.
Una breve historia de un número cuyo cuadrado es 2.
¡La de matemáticas que hay en un folio! ¿Sabes de dónde proviene el formato de hojas A4?.
No es necesario estar vinculado al sector de las Artes Gráficas o al mundo del diseño para estar en contacto diario con el sistema de clasificación o medidas de papel DIN A. Seguramente si alguna vez habrás tenido que imprimir un documento o imagen en un tamaño en concreto. Y en algún momento nos hemos preguntado si nuestra impresora podría tolerar ese tamaño de impresión. Estamos habituados a escuchar que si tal o cual formato está en A4, A3, A5, etc. ¿pero de qué manera funcionan todos? ¿cuál es su origen y sus utilidades? A continuación respondemos a estas preguntas.
DIN no es más que un acrónimo que significa Deutches Institut für Normung, que traducido significa Instituto Alemán de Normalización. Esta entidad que surgió en 1917 es la encargada de dictar los estándares o normas técnicas en Alemania. Dichas normas tienen como finalidad exclusiva asegurar y garantizar la calidad de aquello que se quiere normalizar, en este caso el tamaño del papel. Aunque quizás pienses que la normativa DIN sólo hace referencia al formato del papel, lo cierto es que existen y puedes encontrar aproximadamente 30.000 normativas DIN en este 2016 según archivo.
Fue el ingeniero berlinés Walter Porstmann quien estableció hacia el año 1922 las medidas DIN A a partir de la incorporación de la normativa DIN 476. El propósito era estandarizar de alguna manera los diferentes formatos de papel o página para aprovechar el máximo de papel y que hubiera el mínimo desperdicio posible. Dentro de la misma normativa DIN 476 encontramos la serie A, donde se definen precisamente estas medidas. Junto a la serie A también existen otras cuatro plantillas B, C, D y E y cada una de ellas contiene una numeración de varios tamaños: 0, 1, 2, 3, 4, 5, etc.
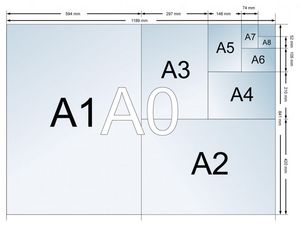
Las medidas DIN A parten de un formato referente que es el A0. El resto de formatos y series se calculan siempre a partir de éste.
En la serie A, al tamaño de papel de 1 m2 se le llama A0. Las divisiones posteriores que disminuyen la superficie a la mitad, reciben el nombre de A1, A2, A3, A4, etc. Lo que en realidad está indicando la numeración asociada a la letra A es la cantidad de cortes a la mitad desde la hoja original. Así por ejemplo, una hoja tamaño A4 tiene una superficie igual a la mitad de una hoja medida A3.
Cuando se corta por la mitad una hoja en tamaño A0 (1 m2), el lado más corto se convierte en la parte más larga de la hoja resultante (A1). Por tanto, si cortamos cualquier hoja de la serie a la mitad de su lado más largo, obtendremos siempre dos hojas del tamaño siguiente, que al mismo tiempo mantienen perfectamente las proporciones entre el ancho y el largo, siendo la razón de proporcionalidad igual a la raíz cuadrada de 2. Es decir, para cualquier formato DIN A, si dividimos el largo entre el ancho, nos dará (aproximadamente) 1,4142.
Puedes hacer la prueba: Mide el ancho y largo de una hoja tamaño DIN A4 y verás que se cumple la proporción; dóblala por el lado más largo y pártela por la mitad, mide el ancho y el largo de una de las mitades, divide las dos cifras y verás que se sigue cumpliendo: 1,4142.
Veamos la demostración:
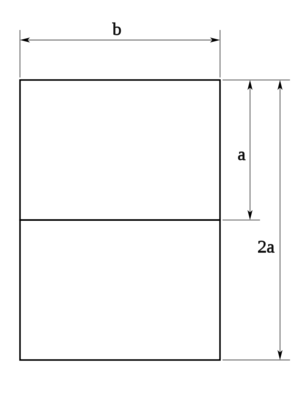
Partiendo de un formato de lados a y b, el formato superior tendrá 2a por b, para que la proporción entre sus lados sea la misma tendrá que cumplirse que:
Esto es:
Si la proporción entre el lado mayor y menor es raíz de dos, cortando un formato en dos iguales esta proporción se conserva.
Si el formato A0 tiene una superficie de un metro cuadrado, tendremos:
Sabiendo el valor de a el cálculo de b es inmediato:
Lo que podemos resumir como regla mnemotécnica que el formato DIN A0, tiene por medidas:
Dividiendo el lado mayor entre dos, obtendremos sucesivamente los distintos formatos A1, A2, A3, A4 ...
Exraido de: blog.imprentaonline24.es y wikipedia.es
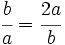
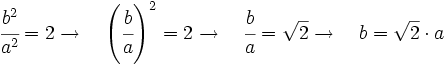
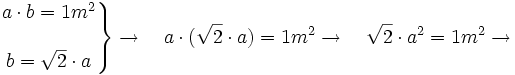
![a^2 = \cfrac{1m^2}{\sqrt{2}} \rightarrow \quad a = \sqrt{\cfrac{1m^2}{\sqrt{2}}} = \cfrac{1m}{\sqrt[4]{2}} = \cfrac{1}{1,189} \; m = 0,841 \; m](/wikipedia/images/math/e/d/6/ed67279193d5f651e1b3f739d1f96eb0.png)
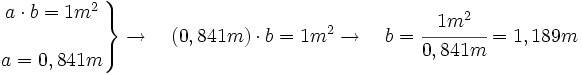
![DIN \; A0 \quad \left \{ \begin{matrix} ancho = \cfrac{1}{\sqrt[4]{2}} \; m \\ \\ largo = \sqrt[4]{2} \; m \end{matrix} \right .](/wikipedia/images/math/9/6/3/96380202caaa3fd258db9e669b1fa5c6.png)

