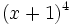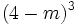Fórmula del binomio de Newton (1ºBach)
De Wikipedia
| Revisión de 09:42 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) |
||
| Línea 1: | Línea 1: | ||
| + | {{Menú Matemáticas 1BT | ||
| + | |ir= | ||
| + | |ampliar= | ||
| + | |repasar= | ||
| + | |enlaces= | ||
| + | }} | ||
| + | __TOC__ | ||
| + | {{p}} | ||
| + | (pág 45) | ||
| ==Binomio de Newton== | ==Binomio de Newton== | ||
| - | {{Teorema_sin_demo|titulo=Teorema: ''Fórmula del binomio de Newton''|enunciado=:El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula: | + | {{Tabla75|celda2=[[Imagen:Triangulo_Pascal_3.jpg|thumb|270px|Triángulo de Pascal en el escrito original de Pascal.]] |
| + | |celda1= | ||
| + | {{Teorema|titulo=Teorema: ''Fórmula del binomio de Newton''|enunciado=El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula: | ||
| <br> | <br> | ||
| <center><math>(a+b)^n = {n \choose 0}a^n + {n \choose 1}a^{n-1}b^1 + {n \choose 2}a^{n-2}b^2 + \cdots + {n \choose n-1}a^1 b^{n-1} + {n \choose n} b^n, | <center><math>(a+b)^n = {n \choose 0}a^n + {n \choose 1}a^{n-1}b^1 + {n \choose 2}a^{n-2}b^2 + \cdots + {n \choose n-1}a^1 b^{n-1} + {n \choose n} b^n, | ||
| </math></center> | </math></center> | ||
| <br> | <br> | ||
| - | :que podemos expresar de forma abreviada de la siguiente manera: | + | que podemos expresar de forma abreviada de la siguiente manera: |
| <center><math>(a+b)^n = \sum_{k=0}^n {n \choose k}a^{n-k}b^k </math></center> | <center><math>(a+b)^n = \sum_{k=0}^n {n \choose k}a^{n-k}b^k </math></center> | ||
| - | }} | ||
| - | |||
| - | Atribuido a [[Newton]], el teorema fue en realidad descubierto por primera vez por [[Al-Karaji]] alrededor del año 1000. | ||
| - | |||
| - | ===Coeficientes binomiales=== | ||
| - | {{Tabla75|celda2=[[Imagen:Triangulo_Pascal_1.gif|Triángulo de Pascal para ''n=3''.]] | ||
| - | |celda1={{Caja_Amarilla|texto=Llamaremos '''coeficientes binomiales''' a los coeficientes <math>{n \choose k}</math>, de los términos del desarrollo del binomio de Newton.}} | ||
| - | {{p}} | ||
| - | {{Teorema sin demo|titulo=Propiedad: ''Relación entre los coeficientes binomiales''|enunciado=:Los coeficientes binomiales cumplen la siguiente relación: | ||
| - | |||
| - | <center><math> {n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}</math></center> | ||
| + | siendo<math>{n\choose k}</math>, los [[Factoriales y números combinatorios (1ºBach)#Coeficientes binomiales | coeficientes binomiales]]. | ||
| + | |demo= | ||
| + | {{Video_enlace | ||
| + | |titulo1=Demostración | ||
| + | |duracion=22'02" | ||
| + | |sinopsis=Demostración por el método de inducción matemática de la fórmula del Binomio de Newton. | ||
| + | |url1=https://youtu.be/6i01gtbOA-s | ||
| }} | }} | ||
| }} | }} | ||
| + | Atribuido a [[Newton]], el teorema fue en realidad descubierto por primera vez por [[Al-Karaji]] alrededor del año 1000. | ||
| + | }} | ||
| + | {{p}} | ||
| ===Triángulo de Pascal=== | ===Triángulo de Pascal=== | ||
| {{Tabla75|celda2= | {{Tabla75|celda2= | ||
| - | [[Imagen:Triangulo_Pascal.png|thumb|235px|Triángulo de Pascal para ''n=10''.]] | + | [[Imagen:Triangulo_Pascal.png|thumb|210px|Triángulo de Pascal para ''n=10''.]] |
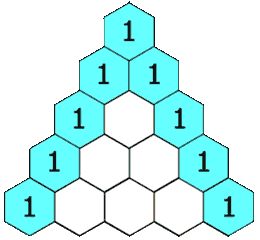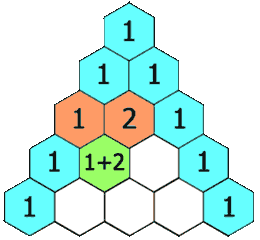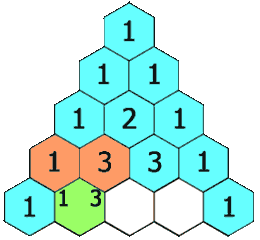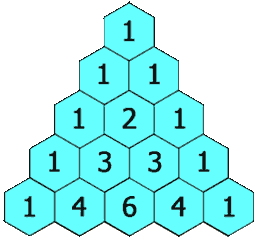
| - | |celda1={{Caja_Amarilla|texto=El '''triángulo de Pascal''' es una representación de los coeficientes binomiales <math>{n \choose k}</math> ordenados en forma triangular. | + | <center>[[Imagen:Triangulo_Pascal_1.gif|Triángulo de Pascal para ''n=3''.]]</center> |
| + | |celda1= | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto=El '''triángulo de Pascal''' es una representación de los coeficientes binomiales ordenados en forma triangular. | ||
| <center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Línea 41: | Línea 54: | ||
| . \ . \ . \ . \ . \ . \ . \ . \ . \ . \ . \ . | . \ . \ . \ . \ . \ . \ . \ . \ . \ . \ . \ . | ||
| \end{matrix}\;</math></center> | \end{matrix}\;</math></center> | ||
| + | {{p}} | ||
| + | }} | ||
| + | {{p}}Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, en los siglos X y XI, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. | ||
| + | También conocido como '''triángulo de Tartaglia''', especialmente en Italia, en honor al algebrista italiano[[ Tartaglia | Niccolò Fontana Tartaglia]] (1500–77). | ||
| + | <br> | ||
| + | {{Teorema|titulo=Propiedades|enunciado= | ||
| + | # Cada casilla del triángulo se obtiene como suma de las dos que hay justo encima de ella. | ||
| + | # Los coeficientes del desarrollo de (''a''+''b'')<sup>''n''</sup> se encuentran en la línea "''n''+1" del triángulo de Pascal. | ||
| + | # El triángulo de Pascal es simétrico. | ||
| + | # La suma de todos los valores de la fila "''n''" del triángulo de Pascal es igual a 2<sup>n. | ||
| + | |demo= | ||
| + | #Esto es así porque <math> {n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}</math>. [1] | ||
| + | #Esto es inmediato, por como está construido el triángulo de Pascal. | ||
| + | #Esto es así porque <math>{n\choose {n-p}} = {n\choose p}</math>. [2] | ||
| + | #Esto es debido a que, por la fórmula del binomio de Newton aplicada al binomio (1+1)<sup>n</sup>: | ||
| + | {{p}} | ||
| + | <center><math>2^n = (1+1)^n= {n \choose 0} + {n \choose 1} + \cdots +{n \choose n-1} + {n \choose n} </math></center> | ||
| - | Cada casilla del triángulo se obtiene como suma de las dos que hay justo encima de ella. (Por la propiedad anterior) | + | :[1] y [2] son [[Factoriales y números combinatorios (1ºBach)#Propiedades de los números combinatorios | propiedades de los coeficientes binomiales]] |
| + | }} | ||
| + | {{Video_enlace_derivando | ||
| + | |titulo1=Los secretos del triángulo de Pascal | ||
| + | |duracion=4'23" | ||
| + | |sinopsis=El triángulo de Pascal contiene sorprendentes propiedades y curiosidades para disfrutar de las matemáticas. | ||
| + | |url1=https://youtu.be/DPxIbJ-Rbf4 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Binomio de Newton|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=19'39" | ||
| + | |sinopsis=Tutorial en el que se explica la construcción del Triángulo de Pascal o Triángulo de Tartaglia y se aplica para el desarrollo de potencias de binomios. También se explica la relación con el Binomio de Newton. | ||
| + | |url1=https://www.youtube.com/watch?v=yPdEiGNfA-4&index=12&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2a | ||
| + | |duracion=4'30" | ||
| + | |sinopsis=Qué es el Binomio de Newton. | ||
| + | |url1=https://youtu.be/2upmZRE0goU?list=PLwCiNw1sXMSBoOd1N4rcHAmaUyI-W_6GK | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2b | ||
| + | |duracion=11'17" | ||
| + | |sinopsis=Fórmula del Binomio de Newton. | ||
| + | |url1=https://youtu.be/6h4azotMxnc?list=PLwCiNw1sXMSBoOd1N4rcHAmaUyI-W_6GK | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2c | ||
| + | |duracion=8'05" | ||
| + | |sinopsis=El triángulo de Tartaglia. | ||
| + | |url1=https://youtu.be/3AHIVxLt7Q8?list=PLwCiNw1sXMSBoOd1N4rcHAmaUyI-W_6GK | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=13'59" | ||
| + | |sinopsis=Desarrolla las siguientes potencias usando el binomio de Newton: | ||
| + | a) <math>\left(x-5 \right)^3</math> | ||
| + | b) <math>\left(2x+3 \right)^4</math> | ||
| + | |||
| + | c) <math>\left(3x-x^2 \right)^5</math> | ||
| + | |||
| + | d) <math>\left(x^2+\cfrac{4}{x} \right)^3</math> | ||
| + | |url1=https://youtu.be/Wts9KnAXHis?list=PLwCiNw1sXMSBoOd1N4rcHAmaUyI-W_6GK | ||
| }} | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=13'59" | ||
| + | |sinopsis= | ||
| + | a) Halla el 6º término del desarrollo de <math>\left(x-3 \right)^8</math>. | ||
| + | |||
| + | b) Halla el coeficiente de <math>x^5\;</math> en el desarrollo de <math>\left(2x-\cfrac{1}{x} \right)^7</math>. | ||
| + | |url1=https://youtu.be/EeSF8zODy7s?list=PLwCiNw1sXMSBoOd1N4rcHAmaUyI-W_6GK | ||
| }} | }} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=8'19" | ||
| + | |sinopsis=Desarrolla usando el triángulo de Tartaglia y números combinatorios: | ||
| - | Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. | + | <math>(x-3)^5\;</math> |
| + | |url1=http://www.unicoos.com/video/matematicas/4-eso/combinatoria/binomio-de-newton/binomio-de-newton | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=4'15" | ||
| + | |sinopsis=Desarrolla la siguiente potencia usando el binomio de Newton: | ||
| - | {{Teorema|titulo=Propiedades|enunciado= | + | :<math>(x+1)^4\;</math> |
| - | # Los coeficientes del desarrollo de (''a''+''b'')<sup>''n''</sup> se encuentran en la línea "''n''+1" del Triángulo de Pascal. | + | |url1=https://www.youtube.com/watch?v=DWSEskmqz94&index=2&list=PLF5FF72F715845049 |
| - | # El Triángulo de Pascal es simétrico. | + | }} |
| - | # La suma de todos los valores de la fila "''n''" es igual a 2<sup>n. | + | {{Video_enlace_childtopia |
| - | |demo= | + | |titulo1=Ejercicio 5 |
| - | #Esto es inmediato, por como está construido el Triángulo de Pascal. | + | |duracion=4'19" |
| - | #Esto es así porque <math>{n\choose {n-p}} = {n\choose p}.</math>. | + | |sinopsis=Desarrolla la siguiente potencia usando el binomio de Newton: |
| - | #Esto es debido a que, por el teorema del binomio, la expansión de la ''n''-potencia de (1 + 1)<sup>''n''</sup> = 2<sup>''n''</sup> es | + | |
| + | :<math>(4-m)^3\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=a7irZWthLb8&index=1&list=PLF5FF72F715845049 | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=11'17" | ||
| + | |sinopsis=Desarrolla usando el triángulo de Tartaglia y por otro método: | ||
| + | |||
| + | a) <math>(a+b)^6\;</math> | ||
| + | |||
| + | b) <math>(x-y)^5\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=W3idpDs9y4E&list=PL9B9AC3136D2D4C45&index=24 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 7 | ||
| + | |duracion=15´23" | ||
| + | |url1=https://www.youtube.com/watch?v=KV2TlE7KdVk&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=53 | ||
| + | |sinopsis=Desarrolla usando el triángulo de Tartaglia: <math>(a+b)^5\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 8 | ||
| + | |duracion=10´08" | ||
| + | |url1=https://www.youtube.com/watch?v=vmv0VIBglc4&index=54&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis= | ||
| + | a) Halla el segundo término del desarrollo por el binomio de Newton de <math>(2x^2+1)^6\;</math> | ||
| + | |||
| + | b) Halla el coeficiente del quinto término del desarrollo por el binomio de Newton de <math>(3a+b)^6\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 9 | ||
| + | |duracion=10´10" | ||
| + | |url1=https://www.youtube.com/watch?v=J90qsLwUEDA&index=55&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis= | ||
| + | a) Halla el término independiente del desarrollo por el binomio de Newton de <math>\left( x^2+\cfrac{1}{x^2}\right)^6\;</math> | ||
| + | |||
| + | b) La diferencia del número de términos de los binomios <math>(a+b)^m\;</math> y <math>(a+b)^n\;</math> es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n". | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 10 | ||
| + | |duracion=16´49" | ||
| + | |url1=https://www.youtube.com/watch?v=xUy-7vmdXyE&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=56 | ||
| + | |sinopsis= | ||
| + | a) Si los coeficientes del primer y último término del desarrollo de <math>P(x,y)=(2a^2x^2+ay^5)^{16}\;</math> son iguales, halla el coeficiente del término 14. | ||
| + | |||
| + | b) Al desarrollar el binomio <math>\left( \cfrac{x^m}{y^{n-10}}+\cfrac{y^{n+20}}{x} \right)^n\;</math> se obtiene un único término central, cuya parte literal es <math>x^{120}y^{720}\;</math>. Halla el valor de <math>m+n\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1= Ejercicio 11 | ||
| + | |duracion=9´57" | ||
| + | |url1=https://www.youtube.com/watch?v=tTS6yKVHxNI&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=57 | ||
| + | |sinopsis=Halla <math>a^5+b^5\;</math> sabiendo que <math>a+b=\sqrt{5}</math> y que <math>a \cdot b=5</math>. | ||
| + | }} | ||
| + | {{Video_enlace_fisicaymates | ||
| + | |titulo1= Ejercicio 12 | ||
| + | |duracion=13´36" | ||
| + | |url1=https://www.youtube.com/watch?v=DNRMG6AmX9Q&index=3&list=PLaJK82VXGZpSsri2iLpaauCwe_1FFMDJI | ||
| + | |sinopsis=Desarrolla <math>\left(x-\cfrac{1}{x} \right)^4</math>. | ||
| + | }} | ||
| + | {{Video_enlace_fisicaymates | ||
| + | |titulo1= Ejercicio 13 | ||
| + | |duracion=19´04" | ||
| + | |url1=https://www.youtube.com/watch?v=7hKPrsfSG5Y&list=PLaJK82VXGZpSsri2iLpaauCwe_1FFMDJI&index=4 | ||
| + | |sinopsis=Halla el cuarto término del desarrollo de <math>\left(4x^2-5xy \right)^7</math>. | ||
| + | }} | ||
| + | {{Video_enlace_fisicaymates | ||
| + | |titulo1= Ejercicio 14 | ||
| + | |duracion=11´52" | ||
| + | |url1=https://www.youtube.com/watch?v=9J4Gl2S4zAk&list=PLaJK82VXGZpSsri2iLpaauCwe_1FFMDJI&index=5 | ||
| + | |sinopsis=Halla el coeficiente del término 20 del desarrollo de <math>\left(3x-y \right)^{30}</math>. | ||
| + | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1= Ejercicio 15 | ||
| + | |duracion=4´30" | ||
| + | |url1=https://youtu.be/FDow6U2_Zxo | ||
| + | |sinopsis=Halla el 6º término del desarrollo de <math>\left(\cfrac{1}{3}-3x \right)^9</math>. | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejercicio 16 | ||
| + | |duracion=19'39" | ||
| + | |sinopsis=Desarrolla las siguientes potencias usando el binomio de Newton: | ||
| + | |||
| + | a) <math>(x^2+2x)^4\;</math> | ||
| + | |||
| + | b) <math>(a-b)^5\;</math> | ||
| + | |||
| + | c) <math>(x^2-3x)^6\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=9jN538iatAM | ||
| + | }} | ||
| + | |||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | <center><math> {n \choose 0} + {n \choose 1} + \cdots +{n \choose n-1} + {n \choose n} = 2^n, </math></center> | + | {{wolfram desplegable|titulo=Binomio de Newton|contenido= |
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Binomio de Newton'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | Halla el desarrollo de (a+b)<sup>7</sup>. | ||
| + | |||
| + | {{p}} | ||
| + | |sol=Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: | ||
| + | |||
| + | :{{consulta|texto=expand (a+b)^7}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Ejercicios== | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación: ''Binomio de Newton'' | ||
| + | |descripcion=Autoevaluación sobre el binomio de Newton. | ||
| + | |url1=http://www.vitutor.com/pro/1/a_11_e.html | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Binomio de Newton'' | ||
| + | |cuerpo= | ||
| + | (Pág. 45) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 1b | ||
| + | [[Imagen:yellow_star.png|12px]] 1a,c; 2 | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(pág 45)
Binomio de Newton
Teorema: Fórmula del binomio de Newton El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula:
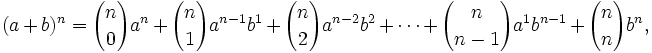
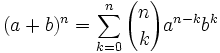 siendo Demostración: Demostración por el método de inducción matemática de la fórmula del Binomio de Newton. Atribuido a Newton, el teorema fue en realidad descubierto por primera vez por Al-Karaji alrededor del año 1000. |
Triángulo de Pascal
|
El triángulo de Pascal es una representación de los coeficientes binomiales ordenados en forma triangular. 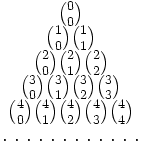 También conocido como triángulo de Tartaglia, especialmente en Italia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77).
Propiedades
Demostración:
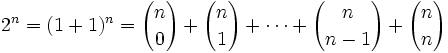
El triángulo de Pascal contiene sorprendentes propiedades y curiosidades para disfrutar de las matemáticas. |
Tutorial en el que se explica la construcción del Triángulo de Pascal o Triángulo de Tartaglia y se aplica para el desarrollo de potencias de binomios. También se explica la relación con el Binomio de Newton.
Qué es el Binomio de Newton.
Fórmula del Binomio de Newton.
El triángulo de Tartaglia.
Desarrolla las siguientes potencias usando el binomio de Newton:
a) 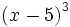
b) 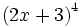
c) 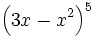
d) 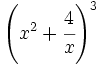
a) Halla el 6º término del desarrollo de 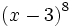 .
.
b) Halla el coeficiente de 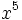 en el desarrollo de
en el desarrollo de 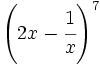 .
.
Desarrolla usando el triángulo de Tartaglia y números combinatorios:
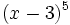
Desarrolla la siguiente potencia usando el binomio de Newton:
Desarrolla la siguiente potencia usando el binomio de Newton:
Desarrolla usando el triángulo de Tartaglia y por otro método:
a) 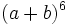
b) 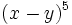
Desarrolla usando el triángulo de Tartaglia: 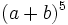
a) Halla el segundo término del desarrollo por el binomio de Newton de 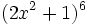
b) Halla el coeficiente del quinto término del desarrollo por el binomio de Newton de 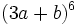
a) Halla el término independiente del desarrollo por el binomio de Newton de 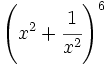
b) La diferencia del número de términos de los binomios 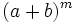 y
y 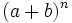 es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n".
es 2; y el producto de dichos binomios posee tres términos más que el primero. Halla "m" y "n".
a) Si los coeficientes del primer y último término del desarrollo de 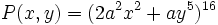 son iguales, halla el coeficiente del término 14.
son iguales, halla el coeficiente del término 14.
b) Al desarrollar el binomio 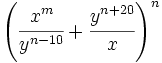 se obtiene un único término central, cuya parte literal es
se obtiene un único término central, cuya parte literal es 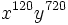 . Halla el valor de
. Halla el valor de 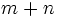 .
.
Halla 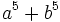 sabiendo que
sabiendo que 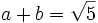 y que
y que 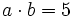 .
.
Desarrolla 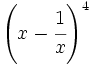 .
.
Halla el cuarto término del desarrollo de 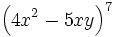 .
.
Halla el coeficiente del término 20 del desarrollo de 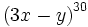 .
.
Halla el 6º término del desarrollo de 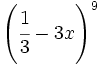 .
.
Desarrolla las siguientes potencias usando el binomio de Newton:
a) 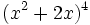
b) 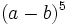
c) 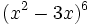
Ejercicios
Autoevaluación sobre el binomio de Newton.
Ejercicios propuestos
|
Ejercicios propuestos: Binomio de Newton |
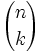 , los
, los 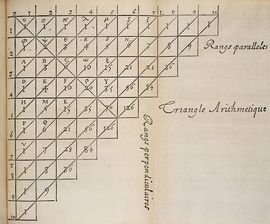
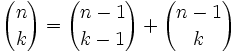 . [1]
. [1]
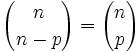 . [2]
. [2]