Plantilla:Término general de una progresión geométrica
De Wikipedia
| Revisión de 18:19 27 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 59: | Línea 59: | ||
| |sinopsis=Tutorial en el que se explica y trabajan las progresiones geométricas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas. | |sinopsis=Tutorial en el que se explica y trabajan las progresiones geométricas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas. | ||
| |url1=https://www.youtube.com/watch?v=kzD175jphZU&index=5&list=PLZNmE9BEzVIkITepuGQcKXJ-FuD5p7cP5}} | |url1=https://www.youtube.com/watch?v=kzD175jphZU&index=5&list=PLZNmE9BEzVIkITepuGQcKXJ-FuD5p7cP5}} | ||
| - | {{Video_enlace_fonemato | + | {{Video_enlace_pildoras |
| |titulo1=Tutorial 3 | |titulo1=Tutorial 3 | ||
| + | |duracion=12'34" | ||
| + | |sinopsis=Término general de una progresión geométrica: Obtención y ejemplos. | ||
| + | |url1=https://youtu.be/Bp7NK6Oi59Y?list=PLwCiNw1sXMSBhPnvO9i-OTkq_sZu71YLG | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 4 | ||
| |duracion=11'41" | |duracion=11'41" | ||
| |url1=https://www.youtube.com/watch?v=YM4635hiMpk&list=PL25FE213AC8622E21&index=12 | |url1=https://www.youtube.com/watch?v=YM4635hiMpk&list=PL25FE213AC8622E21&index=12 | ||
| Línea 79: | Línea 85: | ||
| |url1=https://youtu.be/DuEQ46JgEYY | |url1=https://youtu.be/DuEQ46JgEYY | ||
| |sinopsis=Halla el término general y la forma recursiva de la siguiente progresión geométrica: {168, 84, 42, , 21, ...}. | |sinopsis=Halla el término general y la forma recursiva de la siguiente progresión geométrica: {168, 84, 42, , 21, ...}. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=6´39" | ||
| + | |url1=https://youtu.be/GcUGwpqFaHA | ||
| + | |sinopsis=Halla la fórmula recursiva a partir del término general <math>g_n=9 \cdot 8^{n-1}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=9´35" | ||
| + | |url1=https://youtu.be/Sz6-AQkNGgg | ||
| + | |sinopsis=Problema sobre progresiones geométricas. | ||
| }} | }} | ||
| }} | }} | ||
| Línea 86: | Línea 104: | ||
| |descripcion=Actividades en las que aprenderás a obtener el término general de una progresión geométrica. | |descripcion=Actividades en las que aprenderás a obtener el término general de una progresión geométrica. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena5/3quincena5_contenidos_3b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena5/3quincena5_contenidos_3b.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 2 | ||
| + | |descripcion=Progresiones geométricas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-geometric-sequences/a/geometric-sequences-review | ||
| }} | }} | ||
| {{AI_Khan | {{AI_Khan | ||
| Línea 96: | Línea 119: | ||
| |descripcion=Halla el término general de una progresión geométrica. | |descripcion=Halla el término general de una progresión geométrica. | ||
| |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-geometric-sequences/e/sequences-as-functions | |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-geometric-sequences/e/sequences-as-functions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 3 | ||
| + | |descripcion=Convertir formas recursivas y explícitas de sucesiones geométricas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/sequences/constructing-geometric-sequences/e/explicit-and-recursive-formulas-of-geometric-sequences | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 4 | ||
| + | |descripcion=Problemas verbales con progresiones geométricas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/sequences/modeling-with-sequences/e/recursive_explicit | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
Término general de una progresión geométrica
El término general, 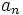 , de una progresión geométrica de razón
, de una progresión geométrica de razón  es:
es:
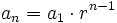
En efecto, de forma intuitiva:
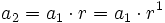

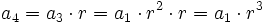
........................
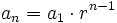
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
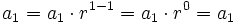
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
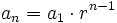 . [1]
. [1]Por ser una progresión geométrica cada término se obtiene multiplicando por r el anterior término:
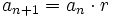 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n \cdot r \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 \cdot r^{n-1} \cdot r =a_1 \cdot r^{((n+1)-1)}](/wikipedia/images/math/b/5/0/b50e2fb51571873946095ab7579f8b90.png)
- Definición de progresión geométrica.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones geométricas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Término general de una progresión geométrica: Obtención y ejemplos.
- Definición de progresión geométrica.
- Ejemplos.
- Término general de una progresión geométrica.
Una progresión geométrica tiene como término general 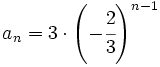 , halla el término
, halla el término 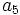 .
.
Halla el término general y la forma recursiva de la siguiente progresión geométrica: {168, 84, 42, , 21, ...}.
Halla la fórmula recursiva a partir del término general 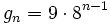 .
.
Problema sobre progresiones geométricas.
Actividades en las que aprenderás a obtener el término general de una progresión geométrica.
Progresiones geométricas.
Usa el término general de una progresión geométrica.
Halla el término general de una progresión geométrica.
Convertir formas recursivas y explícitas de sucesiones geométricas.
Problemas verbales con progresiones geométricas.
Ejercicio resuelto: Progresión geométrica
En una progresión geométrica de términos positivos, 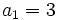 y
y 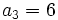 .
Halla
.
Halla  ,
, 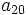 y
y 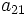 .
.
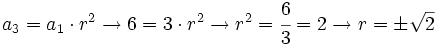
Como la progresión es de términos positivos, sólo nos vale el valor posivo: 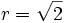 .
.
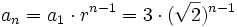
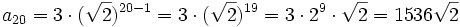
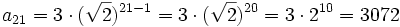
Encuentra el término general de una progresión geométrica dada.

