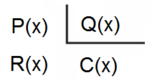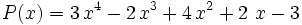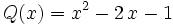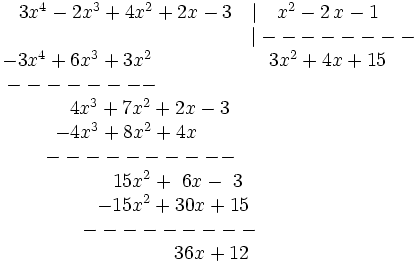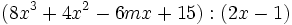Plantilla:División de polinomios
De Wikipedia
| Revisión de 17:14 1 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 56: | Línea 56: | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| - | |duracion=9´ | + | |duracion=8´32" |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/04-division-de-polinomios#.VCMGgBZ8HA8 | + | |url1=https://www.youtube.com/watch?v=Ro2m4Z3vZTA&index=6&list=PL54E0E2B3C3F7EA2B |
| |sinopsis=Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). | |sinopsis=Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). | ||
| De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". | De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". | ||
| Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x). | Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x). | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=17´13" | ||
| + | |url1=https://www.youtube.com/watch?v=zZZuyDhFG5c&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Cómo se hace la división de polinomios | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 4 | ||
| + | |duracion=10´24" | ||
| + | |url1=https://youtu.be/zRnv1BiVMOs?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d | ||
| + | |sinopsis=División de polinomios | ||
| }} | }} | ||
| ---- | ---- | ||
| - | {{Video_enlace_julioprofe | + | {{Video_enlace_clasematicas |
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| + | |duracion=19'10" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | a) <math>(4x^3+2x^2-4x+3):(2x^2-x+1)\;</math> | ||
| + | |||
| + | b) <math>(3x^4-6x^3-2x+1):(3x^2-2)\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=UnjD1hywzjY&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM&index=6#t=3m55s | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 2 | ||
| |duracion=10'30" | |duracion=10'30" | ||
| |sinopsis=Calcula: <math>(6x^5-5x^3-35x-14x^2+23x^4+20):(3x^3-5+x^2)\;</math> | |sinopsis=Calcula: <math>(6x^5-5x^3-35x-14x^2+23x^4+20):(3x^3-5+x^2)\;</math> | ||
| |url1=https://www.youtube.com/watch?v=tc20GDFkPoc&index=13&list=PL9B9AC3136D2D4C45}} | |url1=https://www.youtube.com/watch?v=tc20GDFkPoc&index=13&list=PL9B9AC3136D2D4C45}} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 2 | ||
| - | |duracion=9'59" | ||
| - | |sinopsis=Calcula: <math>(37u^3-15u-8u^2-20u^5):(4u^2-5)\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=8xPi9q549hs&list=PL9B9AC3136D2D4C45&index=14}} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| |titulo1=Ejercicio 3 | |titulo1=Ejercicio 3 | ||
| Línea 87: | Línea 104: | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| - | |duracion=12´ | + | |duracion=12´09" |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/13-polinomios/0401-dos-ejercicios-6#.VCMHQRZ8HA8 | + | |url1=https://www.youtube.com/watch?v=0ExCMeTDnVg&index=7&list=PL54E0E2B3C3F7EA2B|sinopsis=Calcula: |
| - | |sinopsis=Calcula: | + | |
| a) <math>(7x^3-5x^2+3x^5+8x^4+2x-5):(2x^2-1+x^3)\;</math> | a) <math>(7x^3-5x^2+3x^5+8x^4+2x-5):(2x^2-1+x^3)\;</math> | ||
| Línea 95: | Línea 111: | ||
| b) <math>(5x^4+6x^3+8x^2+2x-1):(2x^5+x^3)\;</math> | b) <math>(5x^4+6x^3+8x^2+2x-1):(2x^5+x^3)\;</math> | ||
| }} | }} | ||
| - | ---- | + | {{Video_enlace_julioprofe |
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=9'59" | ||
| + | |sinopsis=Calcula: <math>(37u^3-15u-8u^2-20u^5):(4u^2-5)\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=8xPi9q549hs&list=PL9B9AC3136D2D4C45&index=14 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=8´45" | ||
| + | |url1=https://www.youtube.com/watch?v=6ywMcCGMr7c&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f&index=2 | ||
| + | |sinopsis=Divide los siguientes polinomios entre binomios: | ||
| + | |||
| + | :1a) <math>(x^3-6x^2-5x+2):(x-1)\;</math> | ||
| + | :1b) <math>(x^5-4x^3+x+1):(x^2-1)\;</math> | ||
| + | :1c) <math>(x^6-1):(x^2-1)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=13'34" | ||
| + | |url1=https://www.youtube.com/watch?v=ofDxDp_uv8k&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f&index=3 | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :2a) <math>(x^2+2x+1):x\;</math> | ||
| + | :2b) <math>(x^3+2x^2+4x+2):x^2\;</math> | ||
| + | :2c) <math>(4x^6+2x^5-2x^4):2x^2\;</math> | ||
| + | :2d) <math>(x^5+5x^4+2x^3+13x^2+13x+2):(x^3+3x-2)\;</math> | ||
| + | :2e) <math>(3x^4+x^3+5x^2+x-5):(x^2-3x+1)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=13'26" | ||
| + | |url1=https://www.youtube.com/watch?v=3vVZqzOWCiU&index=4&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :3a) <math>(x^6+5x^4+3x^2-2x):(x^2-x+3)\;</math> | ||
| + | :3b) <math>(x^5+x^4+x^3+x+1):(x+1)\;</math> | ||
| + | |||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=12'27" | ||
| + | |url1=https://www.youtube.com/watch?v=BRyCmJ2TchE&index=5&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :3c) <math>(x^6+2x^5-3x^4+6x-8):(x-3)\;</math> | ||
| + | :3d) <math>(x^3-+x^2+x-1):(x^2-1)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=10'46" | ||
| + | |url1=https://www.youtube.com/watch?v=dUneWW495Lw&index=6&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :4a) <math>(x^5-3x^4-2x^3+x^2-x+1):(x-8)\;</math> | ||
| + | :4b) <math>(2x^4+3x^2+6x-7):(x-1)\;</math> | ||
| + | :4c) <math>(x^3+5x^2+x-1):(x-2)\;</math> | ||
| + | :4d) <math>(x^3+x^2-x-2):(x-1)\;</math> | ||
| + | |||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 12 | ||
| + | |duracion=9'47" | ||
| + | |url1=https://www.youtube.com/watch?v=yuyD3brc_Pk&index=7&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :5a) <math>(2x^6+10x^4-3x^3+2x^2-6):6x^4\;</math> | ||
| + | :5b) <math>(\cfrac{6}{5}x^6+\cfrac{4}{3}x^4+2x^2-\cfrac{6}{3}):6x^4\;</math> | ||
| + | :5c) <math>(3x^4+10x^3-8x^2+6x):x^2\;</math> | ||
| + | :5d) <math>(\cfrac{1}{2}x^3+6x^2-3x+8):\cfrac{1}{3}x\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 13 | ||
| + | |duracion=10'20" | ||
| + | |url1=https://www.youtube.com/watch?v=6EhL5ms9EWU&index=8&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :6a) <math>(4x^2-6x-4):(x-2)\;</math> | ||
| + | :6b) <math>(8x^5-4x^4-3x^2+6x-1):(x^3+3x-1)\;</math> | ||
| + | :6c) <math>(\cfrac{4}{3}x^3+\cfrac{2}{5}x^2-6x+7):(x^2-5)\;</math> | ||
| + | :6d) <math>(x^3-6x^2-3x+1):(x-1)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 14 | ||
| + | |duracion=10'27" | ||
| + | |url1=https://www.youtube.com/watch?v=QAjb7C3vh4s&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f&index=9 | ||
| + | |sinopsis=Indica qué divisiones de polinomios son exactas: | ||
| + | |||
| + | :7a) <math>(x^3+5x-1):(x+3)\;</math> | ||
| + | :7b) <math>(x^4-1):(x+1)\;</math> | ||
| + | :7c) <math>(x^7-x^6-3x^4+16x^3+47x+3x^5-30x^2-24):(x-1)\;</math> | ||
| + | :7d) <math>(x^4-2x^3+x^2+x-1):(x-1)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 15 | ||
| + | |duracion=14'53" | ||
| + | |url1=https://www.youtube.com/watch?v=Wtzb5eh4RAU&index=10&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :8a) <math>(x^3-6x^2-5x-88):(x-8)\;</math> | ||
| + | :8b) <math>(3x^5+7x^4-3x^2+5):(x-6)\;</math> | ||
| + | :9a) <math>(x^5-32):(x+2)\;</math> | ||
| + | :9b) <math>(x^5-32):(x-2)\;</math> | ||
| + | :9c) <math>(x^4-16):(x+2)\;</math> | ||
| + | |||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 16 | ||
| + | |duracion=12'41" | ||
| + | |url1=https://www.youtube.com/watch?v=cozUbh_Mn3E&list=PLw7Z_p6_h3ow3JMLdFTqb87BGyCgmmd3f&index=11 | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :9d) <math>(x^3-8):(x-2)\;</math> | ||
| + | :9e) <math>(x^3-8):(x+2)\;</math> | ||
| + | :9f) <math>(x^3+8):(x-2)\;</math> | ||
| + | :9g) <math>(x^3+8):(x+2)\;</math> | ||
| + | :9h) <math>(x^3-27):(x-3)\;</math> | ||
| + | :9i) <math>(x^3-27):(x+3)\;</math> | ||
| + | :9j) <math>(x^4+1):(x+1)\;</math> | ||
| + | |||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Ejercicios 17 | ||
| + | |duracion=7´08" | ||
| + | |url1=https://youtu.be/RfAT9v6948A?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d | ||
| + | |sinopsis=Divide los siguientes polinomios: | ||
| + | |||
| + | :a) <math>(3x^3+x^2-4x+7):(x^2-5x+3)\;</math> | ||
| + | :b) <math>(x^4+5x^3-2x+1):(3x^2+4)\;</math> | ||
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Método de Horner|enunciado= | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Método de Horner | + | |titulo1=Tutorial |
| |duracion=12´03 | |duracion=12´03 | ||
| |url1=https://www.youtube.com/watch?v=nfoAh84mdqs&t=304s | |url1=https://www.youtube.com/watch?v=nfoAh84mdqs&t=304s | ||
| |sinopsis=Método de Horner para la división de polinomios | |sinopsis=Método de Horner para la división de polinomios | ||
| }} | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=8´18 | ||
| + | |url1=https://www.youtube.com/watch?v=3JrHMzJpSBs&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=26 | ||
| + | |sinopsis=Calcula: <math>(5x^3+2x^2+1):(x^2+2+2x)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=9´27 | ||
| + | |url1=https://www.youtube.com/watch?v=HO23R-3d_lk&index=28&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis=Halla el resto de la división: | ||
| + | |||
| + | :<math>5x^4 :(x^2-2x-3)\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=9´01 | ||
| + | |url1=https://www.youtube.com/watch?v=UJQF1FibXe0&index=29&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| + | |sinopsis=Halla el resto de la división | ||
| + | |||
| + | :<math>(8x^3+4x^2-6mx+15):(2x-1)\;</math> | ||
| + | |||
| + | sabiendo que la suma de los coeficientes del cociente es 28. | ||
| + | |||
| + | }} | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicios de autoevaluación sobre división de polinomios. | ||
| + | |url1=http://www.vitutor.com/ab/p/coc_3_e.html | ||
| + | |titulo1=Autoevaluación: ''División de polinomios'' | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
La división polinómica es, en ciertos aspectos, similar a la división numérica.
Dados dos polinomios  (dividendo) y
(dividendo) y  (divisor) de modo que el grado de
(divisor) de modo que el grado de  sea mayor o igual que el grado de
sea mayor o igual que el grado de  y el grado de
y el grado de  sea mayor o igual a cero, siempre podremos hallar dos polinomios
sea mayor o igual a cero, siempre podremos hallar dos polinomios 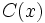 (cociente) y
(cociente) y 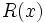 (resto) tales que:
(resto) tales que:
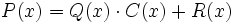
que también podemos representar como:
- El grado de
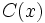 es igual a la diferencia entre los grados de
es igual a la diferencia entre los grados de  y
y  , mientras que el grado de
, mientras que el grado de 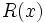 será, como máximo, un grado menor que
será, como máximo, un grado menor que  .
.
- Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.
División de polinomios. Ejemplos.
Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x).
Cómo se hace la división de polinomios
División de polinomios
Calcula:
a) 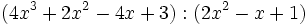
b) 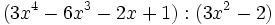
Calcula: 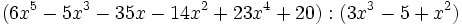
Calcula: 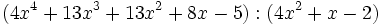
Calcula: 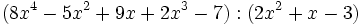
Calcula:
a) 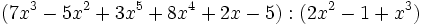
b) 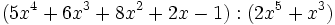
Calcula: 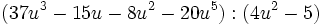
Divide los siguientes polinomios entre binomios:
- 1a)
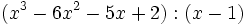
- 1b)
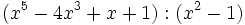
- 1c)
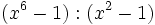
Divide los siguientes polinomios:
- 2a)
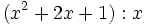
- 2b)
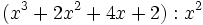
- 2c)
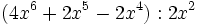
- 2d)
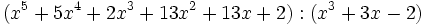
- 2e)
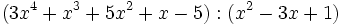
Divide los siguientes polinomios:
- 3a)
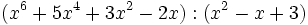
- 3b)
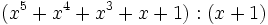
Divide los siguientes polinomios:
- 3c)
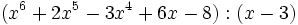
- 3d)
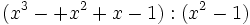
Divide los siguientes polinomios:
- 4a)
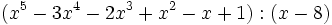
- 4b)
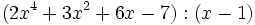
- 4c)
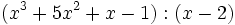
- 4d)
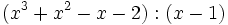
Divide los siguientes polinomios:
- 5a)
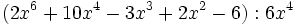
- 5b)
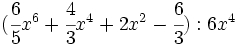
- 5c)
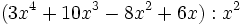
- 5d)
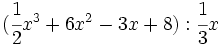
Divide los siguientes polinomios:
- 6a)
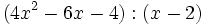
- 6b)
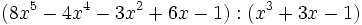
- 6c)
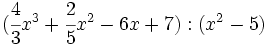
- 6d)
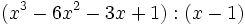
Indica qué divisiones de polinomios son exactas:
- 7a)
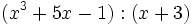
- 7b)
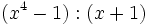
- 7c)
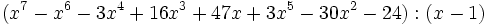
- 7d)
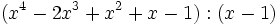
Divide los siguientes polinomios:
- 8a)
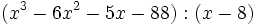
- 8b)
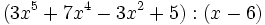
- 9a)
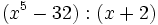
- 9b)
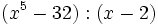
- 9c)
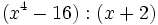
Divide los siguientes polinomios:
- 9d)
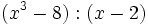
- 9e)
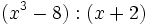
- 9f)
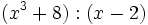
- 9g)
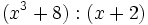
- 9h)
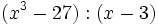
- 9i)
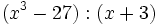
- 9j)
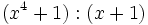
Divide los siguientes polinomios:
- a)
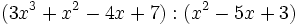
- b)
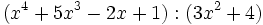
Método de Horner para la división de polinomios
Calcula: 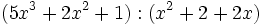
Halla el resto de la división:
Halla el resto de la división
sabiendo que la suma de los coeficientes del cociente es 28.
Ejercicios de autoevaluación sobre división de polinomios.