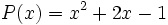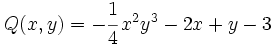Plantilla:Polinomios
De Wikipedia
| Revisión de 06:59 3 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
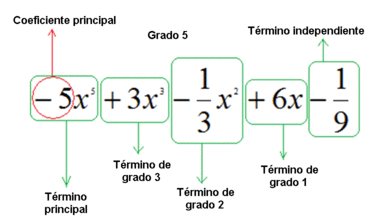
| - | {{Caja_Amarilla|texto= | + | {{Tabla75|celda2=[[Imagen:polinomio.gif|thumb|370px|Elementos y grado de un polinomio]] |
| - | *Un '''polinomio''' es una expresión algebraica que se obtiene al sumar dos o más monomios. A cada monomio se le llama '''término''' del polinomio. Si tiene dos términos se llama '''binomio'''; si tiene tres '''trinomio''', etc. | + | |celda1={{Caja_Amarilla|texto= |
| - | *Se llama '''forma reducida''' de un polinomio, a aquella en la que se ha simplificado, sumando los términos semejantes. | + | *Un '''polinomio''' es una expresión algebraica formada por un monomio o por la suma de varios monomios. A cada monomio se le llama '''término''' del polinomio. Si tiene dos términos se llama '''binomio'''; si tiene tres '''trinomio'''; si tiene cuatro '''cuatrinomio''' etc. |
| - | *Se llama '''grado''' de un polinomio, al mayor de los grados de los monomios que lo componen cuando el polinomio se ha puesto en forma reducida. | + | *Un polinomio se dice que es '''nulo''' si todos los monomios que lo componen tienen coeficiente cero. |
| + | *Un polinomio está dado en '''forma reducida''' si en su expresión no aparecen monomios semejantes, ni nulos. | ||
| + | *Se llama '''grado''' de un polinomio no nulo, al mayor de los grados de los monomios que lo componen cuando el polinomio se ha puesto en forma reducida. Un polinomio nulo tiene grado cero. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | {{Nota|titulo=Notación:|texto= |
| - | a) El polinomio <math>2x^2y+5x^2-1 \;\!</math> está en forma reducida y es un trinomio de grado 3. | + | Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis. |
| - | b) El polinomio <math>2x^2+5x^2-x+1 \;\!</math> no está en forma reducida. Su forma reducida es <math>7x^2-x+1 \;\!</math>. Es de grado 2. | + | |
| + | Por ejemplo: | ||
| + | |||
| + | *<math>P(x)=x^2+2x-1\;</math> | ||
| + | *<math>Q(x,y)=-\cfrac{1}{4}\,x^2y^3 -2x +y-3\;</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Grado de un polinomio|enunciado= | + | {{Ejemplo_simple|titulo=Ejemplos:{{b}}|contenido= |
| - | {{Video_enlace_paps | + | a) El polinomio <math>P(x,y)=2x^2y+5x^2-1 \;\!</math> está en forma reducida y es un trinomio de grado 3. |
| + | |||
| + | b) El polinomio <math>P(x)=2x^2+5x^2-x+1 \;\!</math> no está en forma reducida. Su forma reducida es <math>7x^2-x+1 \;\!</math>. Es de grado 2. | ||
| + | |||
| + | c) Los polinomios constantes, como por ejemplo <math>P(x)=5\;</math>, tienen grado 1. Sin embargo, el polinomio nulo, <math>Q(x)=0\;</math>, tiene grado cero. | ||
| + | |||
| + | d) Los polinomios <math>P(x,y)=5x^2-xy+1 \;\!</math> y <math>Q(x,y)=3x^2-2xy-4 \;\!</math> son semejantes. | ||
| + | |||
| + | e) Los polinomios <math>P(x)=5x^2-x+1 \;\!</math> y <math>Q(x)=1-2x+5x^2+x \;\!</math> son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Polinomios: Elementos, tipos y grado|enunciado= | ||
| + | {{Video_enlace_clasematicas | ||
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| + | |duracion=18'29" | ||
| + | |sinopsis=Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes... | ||
| + | |url1=https://www.youtube.com/watch?v=yIfEj2GjrR0&index=13&list=PLZNmE9BEzVImKUDFE-SsTXvB2FiwalKLM | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=11'43" | ||
| + | |sinopsis=Polinomios. Grado de un polinomio. Ejemplos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=KrAzy15tt3o&list=PL54E0E2B3C3F7EA2B&index=1 | ||
| + | }} | ||
| + | {{Video_enlace_angelmartinez | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=0'54" | ||
| + | |sinopsis=Polinomios. Grado de un polinomio. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=ZwDeLMQz3D8 | ||
| + | }} | ||
| + | {{Video_enlace_paps | ||
| + | |titulo1=Tutorial 4 | ||
| |duracion=8'22" | |duracion=8'22" | ||
| |sinopsis=Aprende a calcular el grado relativo y absoluto de un polinomio. | |sinopsis=Aprende a calcular el grado relativo y absoluto de un polinomio. | ||
| Línea 20: | Línea 58: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=Tutorial 5 |
| |duracion=9'31" | |duracion=9'31" | ||
| |sinopsis=Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio. | |sinopsis=Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio. | ||
| Línea 26: | Línea 64: | ||
| '''Nota:''' Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio. | '''Nota:''' Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio. | ||
| |url1=https://www.youtube.com/watch?v=bEqSbiisXjU&t=199s | |url1=https://www.youtube.com/watch?v=bEqSbiisXjU&t=199s | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 6a | ||
| + | |duracion=7'58" | ||
| + | |sinopsis=Polinomios: términos y tipos de polinomios. Polinomios nulos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=9AEjjmsNHzk&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 6b | ||
| + | |duracion=10'41" | ||
| + | |sinopsis=Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes. | ||
| + | |url1=https://www.youtube.com/watch?v=8RI0Y4tR9K4&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx&index=2 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Tutorial 6c | ||
| + | |duracion=8'50" | ||
| + | |sinopsis=*Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos. | ||
| + | *Valor numérico de un polinomio. | ||
| + | |url1=https://www.youtube.com/watch?v=PXHDE3pXi0E&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx&index=3 | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 7 | ||
| + | |duracion=3'10" | ||
| + | |sinopsis=Polinomios. Monomios. Grado y término independiente de un polinomio. | ||
| + | |url1=https://youtu.be/Rrnl-9tZPbA?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=10'15" | ||
| + | |sinopsis= | ||
| + | 1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen: | ||
| + | |||
| + | :a) <math>2x^2+5x+6\;</math> | ||
| + | :b) <math>3x\;</math> | ||
| + | :c) <math>52x^2+25\;</math> | ||
| + | :d) <math>6x^2-3xy-4\;</math> | ||
| + | :e) <math>5\;</math> | ||
| + | :f) <math>2x+6\;</math> | ||
| + | |||
| + | 2) Expresa en forma reducida los siguientes polinomios: | ||
| + | |||
| + | :a) <math>2x^2+5x-3x^2+6x^2-5+3x\;</math> | ||
| + | :b) <math>4x+6x-2x^2-3+5x^2\;</math> | ||
| + | :c) <math>6x-3+2x^2+4x+2-5x^2\;</math> | ||
| + | :d) <math>8x+3x^2-2-5x^2+x^3-2x+1+4x^2\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=yuSJBdPXGjc&index=4&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=13'20" | ||
| + | |sinopsis= | ||
| + | 3) Indica el grado de cada polinomio: | ||
| + | |||
| + | :a) <math>2x^2+5x+3\;</math> ;{{b4}} b) <math>2x-1\;</math> ;{{b4}} c) <math>3x^3-2x+1\;</math> | ||
| + | :d) <math>2\;</math> ;{{b4}} e) <math>4x\;</math> ;{{b4}} f) <math>5-4x+6x^3-x\;</math> | ||
| + | :g) <math>3x-2x^3\;</math> ;{{b4}} h) <math>0x+3\;</math> ;{{b4}} i) <math>0x\;</math> | ||
| + | |||
| + | 4) Indica cuáles de estos polinomios son iguales: | ||
| + | |||
| + | :a) <math>2x^2+3x-2\;</math> ;{{b4}} b) <math>2x-7\;</math> ;{{b4}} c) <math>7x^3+2x+3\;</math> ;{{b4}} d) <math>2x^2-3x+2\;</math> | ||
| + | :e) <math>-2x+7\;</math> ;{{b4}} f) <math>-2+2x^2+3x\;</math> ;{{b4}} g) <math>2x+7x^3+3\;</math> ;{{b4}} h) <math>7-2x\;</math> | ||
| + | :i) <math>2x^2-2+3x\;</math> ;{{b4}} j) <math>-7+2x\;</math> ;{{b4}} k) <math>3+7x^3+2x\;</math> ;{{b4}} l) <math>-3x+2x^2+2\;</math> | ||
| + | |||
| + | 5) Indica cuáles de estos polinomios son semejantes entre sí: | ||
| + | |||
| + | :a) <math>2x^3+2x-5\;</math> ;{{b4}} b) <math>5x^4+5x^2+5x\;</math> ;{{b4}} c) <math>-5x^2-2x+3\;</math> | ||
| + | :d) <math>-7x^3+3x+3\;</math> ;{{b4}} e) <math>7x+6\;</math> ;{{b4}} f) <math>6x^4-6x^2+5\;</math> | ||
| + | :g) <math>6x^2+4x-1\;</math> ;{{b4}} h) <math>-3x-2\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=dP6BxId2T4c&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx&index=5 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=11'49" | ||
| + | |sinopsis=6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios: | ||
| + | |||
| + | :a) <math>2x-3x^4+2-6x^2\;</math> | ||
| + | :b) <math>-7x-5x^5+92x^2-4x^4+2x^3+1\;</math> | ||
| + | :c) <math>4x^2+6x^3-5-2x+6x^4\;</math> | ||
| + | :d) <math>7x^3+3-5x+6x^2\;</math> | ||
| + | :e) <math>2+3x^2\;</math> | ||
| + | :f) <math>5x-7\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=wXujh2wQNnE&index=6&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'13" | ||
| + | |sinopsis=7) Clasificar polinomios en homogéneos/heterogéneos. | ||
| + | |||
| + | :a) <math>4x^2+2xy\;</math> | ||
| + | |||
| + | :b) <math>2xy+5x-6\;</math> | ||
| + | |||
| + | :c) <math>5x^4+2x^2y^2\;</math> | ||
| + | |||
| + | :d) <math>3x^2y-2y^3+2x\;</math> | ||
| + | |||
| + | :e) <math>6x^3y^2+5y^3x^2+1\;</math> | ||
| + | |||
| + | :f) <math>6x^3y^2+5y^3x^2\;</math> | ||
| + | |||
| + | :g) <math>5x^3-6y^3</math> | ||
| + | |url1=https://youtu.be/A3AuZovTSQ4?list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=2'46" | ||
| + | |sinopsis=Dado el polinomio <math>3x^2-8x+7\;</math>, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos. | ||
| + | |||
| + | |url1=https://youtu.be/khCbYOycSJY | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=2'03" | ||
| + | |sinopsis=Escribe un polinomio que exprese el valor de "p" billetes de 20 pesos, "q" monedas de 10 pesos y "r" monedas de 5 pesos. | ||
| + | |url1=https://youtu.be/ph8XLF_uvG0 | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Polinomios|enunciado= | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 1 | ||
| + | |descripcion=Elementos y grado de un polinomio. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_3a.htm | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 2 | ||
| + | |descripcion=Expresiones algebraicas: monomios y polinomios. | ||
| + | *Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación. | ||
| + | *Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena2/3quincena2_contenidos_1a.htm | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Actividad 3 | ||
| + | |descripcion= | ||
| + | *Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio. | ||
| + | *Actividad en la que aprenderás a escribir polinomios en su forma usual. | ||
| + | *Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio. | ||
| + | |||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena2/3quincena2_contenidos_1b.htm | ||
| + | }} | ||
| + | {{AI_upr | ||
| + | |titulo1=Actividad 4 | ||
| + | |descripcion=Actividad sobre polinomios. | ||
| + | |url1=http://quiz.uprm.edu/cgi-bin/Quiz/oneques.cgi?database=REVIEW/exp_alg_tut/exp_alg_tut2_sp.db&no_ques=9 | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
|
Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis.
Por ejemplo:
a) El polinomio 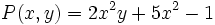 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
b) El polinomio 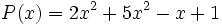 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 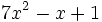 . Es de grado 2.
. Es de grado 2.
c) Los polinomios constantes, como por ejemplo 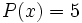 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 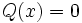 , tiene grado cero.
, tiene grado cero.
d) Los polinomios 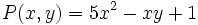 y
y 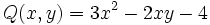 son semejantes.
son semejantes.
e) Los polinomios 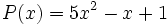 y
y 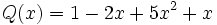 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes...
Polinomios. Grado de un polinomio. Ejemplos.
Polinomios. Grado de un polinomio. Ejemplos.
Aprende a calcular el grado relativo y absoluto de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
- Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos.
- Valor numérico de un polinomio.
Polinomios. Monomios. Grado y término independiente de un polinomio.
1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
- a)
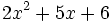
- b)
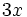
- c)
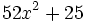
- d)
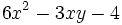
- e)
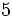
- f)
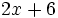
2) Expresa en forma reducida los siguientes polinomios:
- a)
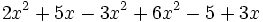
- b)
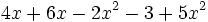
- c)
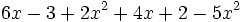
- d)
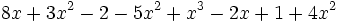
3) Indica el grado de cada polinomio:
- a)
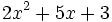 ; b)
; b) 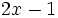 ; c)
; c) 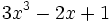
- d)
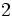 ; e)
; e) 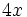 ; f)
; f) 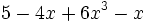
- g)
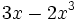 ; h)
; h) 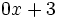 ; i)
; i) 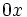
4) Indica cuáles de estos polinomios son iguales:
- a)
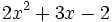 ; b)
; b) 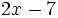 ; c)
; c) 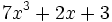 ; d)
; d) 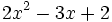
- e)
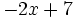 ; f)
; f) 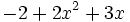 ; g)
; g) 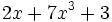 ; h)
; h) 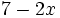
- i)
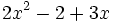 ; j)
; j) 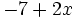 ; k)
; k) 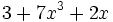 ; l)
; l) 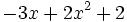
5) Indica cuáles de estos polinomios son semejantes entre sí:
- a)
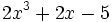 ; b)
; b) 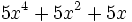 ; c)
; c) 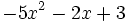
- d)
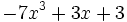 ; e)
; e) 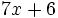 ; f)
; f) 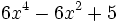
- g)
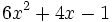 ; h)
; h) 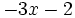
6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
- a)
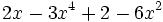
- b)
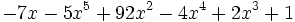
- c)
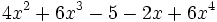
- d)
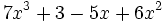
- e)
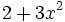
- f)
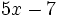
7) Clasificar polinomios en homogéneos/heterogéneos.
- a)
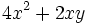
- b)
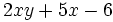
- c)
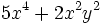
- d)
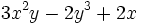
- e)
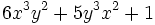
- f)
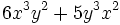
- g) 5x3 − 6y3
Dado el polinomio 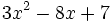 , identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
Escribe un polinomio que exprese el valor de "p" billetes de 20 pesos, "q" monedas de 10 pesos y "r" monedas de 5 pesos.
Elementos y grado de un polinomio.
Expresiones algebraicas: monomios y polinomios.
- Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación.
- Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos.
- Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio.
- Actividad en la que aprenderás a escribir polinomios en su forma usual.
- Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio.
Actividad sobre polinomios.