Plantilla:Inecuación
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:36 12 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 17: | Línea 17: | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Inecuaciones|enunciado= | {{Videotutoriales|titulo=Inecuaciones|enunciado= | ||
| - | {{Video_enlace_khan | + | {{Video_enlace_pildoras |
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| - | |duracion=5'09" | + | |duracion=5'28" |
| - | |sinopsis=Representando desigualdades sencillas en la recta numérica. | + | |sinopsis=Qué son las inecuaciones. |
| - | |url1=https://www.youtube.com/watch?v=gmQtBHZMztw | + | |url1=https://youtu.be/WFGAvvfV-bY?list=PLwCiNw1sXMSBUhnGLJFSf8RU8VKAxVe_R |
| }} | }} | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 32: | Línea 32: | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| |titulo1=Ejercicio | |titulo1=Ejercicio | ||
| - | |duracion=1'37" | + | |duracion=4'52" |
| - | |sinopsis=Representa en la recta numérica los valores de ''x'' que cumplen que ''x<4''. | + | |sinopsis=Comprueba si los valores x=0, x=1, x=2 y x=5 son o no son soluciones de las inecuaciones siguientes: |
| - | |url1=https://www.youtube.com/watch?v=QkrclysEylg | + | |
| + | :a) <math>x+2 \le 2x\;</math> | ||
| + | :b) <math>3x+4>5x\;</math> | ||
| + | |url1=https://www.youtube.com/watch?v=cSALFe1uZvg | ||
| }} | }} | ||
| }} | }} | ||
| - | {{Actividades|titulo=Inecuaciones|enunciado= | ||
| {{AI_Khan | {{AI_Khan | ||
| - | |titulo1=Actividad 1 | + | |titulo1=Autoevaluación |
| - | |descripcion=Representación gráfica de desigualdades en la recta numérica. | + | |descripcion=Verificar soluciones de inecuaciones. |
| - | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-greater-than-less-than/a/graphing-inequalities-review | + | |url1=http://es.khanacademy.org/math/algebra/one-variable-linear-inequalities/alg1-inequalities/e/testing-solutions-of-inequalities |
| - | }} | + | |
| - | {{AI_Khan | + | |
| - | |titulo1=Autoevaluación 1 | + | |
| - | |descripcion=Representación gráfica de desigualdades en la recta numérica. | + | |
| - | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-greater-than-less-than/e/inequalities_on_a_number_line | + | |
| - | }} | + | |
| - | {{AI_Khan | + | |
| - | |titulo1=Autoevaluación 2 | + | |
| - | |descripcion=Problemas verbales de desigualdades. | + | |
| - | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-equations-expressions/pre-algebra-greater-than-less-than/e/inequalities-in-one-variable-1 | + | |
| - | }} | + | |
| - | + | ||
| - | {{AI_vitutor | + | |
| - | |titulo1=Autoevaluación 3 | + | |
| - | |descripcion=Autoevaluación sobre inecuaciones. | + | |
| - | |url1=http://www.vitutor.com/ecuaciones/ine/ine0_Contenidos_e.html | + | |
| - | }} | + | |
| }} | }} | ||
Revisión actual
- Una inecuación es una desigualdad entre expresiones algebraicas.
- Para las desigualdades utilizaremos los símbolos:
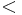(menor que); 
(mayor que); 
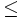(menor o igual que) y 
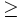(mayor o igual que).
- Las inecuaciones que usan los dos primeros símbolos se llaman inecuaciones estrictas y las que utilizan los dos últimos, inecuaciones no estrictas.
- Si las expresiones algebraicas son polinomios de grado 1, las inecuaciones se llaman lineales y si son de grado 2, cuadráticas.
- Una solución de una inecuación es un conjunto de valores de las variables (uno de cada una) que hace que se cumpla la desigualdad.
- Resolver una inecuación consiste en hallar todas sus soluciones.
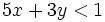es una inecuación lineal estricta con dos incógnitas.
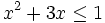es una inecuación cuadrática no estricta con una incógnita.
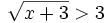es una inecuación estricta con una incógnita.
Tutorial 1 (5'28") Sinopsis:Qué son las inecuaciones.
Tutorial 2 (24'17") Sinopsis: Inecuaciones. Representación de sus soluciones en intervalos o gráficamente. Ejemplos.
Ejercicio (4'52") Sinopsis: Comprueba si los valores x=0, x=1, x=2 y x=5 son o no son soluciones de las inecuaciones siguientes:
- a)
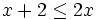
- b)
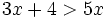
Autoevaluación Descripción: Verificar soluciones de inecuaciones.
