Plantilla:Ramas infinitas de las funciones racionales
De Wikipedia
| Revisión de 17:50 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:32 19 mar 2020 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Consideremos la función racional en la variable x, ya simplificada: | + | {{Teorema_sin_demo|titulo=Proposición|enunciado=Consideremos la función racional en la variable x, ya '''simplificada''' (es decir, si el numerador y el denominador tienen factores comunes, cosa que ocurre si se anulan simultáneamente en algún punto, factorizaremos y simplificaremos dichos factores): |
| {{p}} | {{p}} | ||
| <center><math>f(x)=\cfrac{P(x)}{Q(x)}=\cfrac{a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0}{b_m x^m+b_{m-1}x^{m-1}+ \cdots + b_1 x + b_0}\;</math></center> | <center><math>f(x)=\cfrac{P(x)}{Q(x)}=\cfrac{a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0}{b_m x^m+b_{m-1}x^{m-1}+ \cdots + b_1 x + b_0}\;</math></center> | ||
Revisión de 17:32 19 mar 2020
Proposición
Consideremos la función racional en la variable x, ya simplificada (es decir, si el numerador y el denominador tienen factores comunes, cosa que ocurre si se anulan simultáneamente en algún punto, factorizaremos y simplificaremos dichos factores):
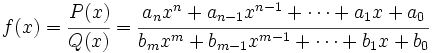
La función 
tiene las siguientes ramas infinitas:
- Asíntotas verticales:
- Si
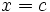es una raíz de Q(x), entonces la recta 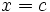es una asíntota vertical de .
- Si
- Asíntotas horizontales:
- Si
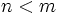, entonces la recta 
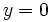es una asíntota horizontal de , tanto por 
, como por 
.
- Si
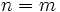, entonces la recta 
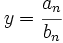es una asíntota horizontal de , tanto por , como por .
- Si
- Asíntotas oblicuas:
- Si
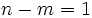, tienen una asíntota oblicua, tanto por , como por . Dicha asíntota es igual al cociente de la división entre 
y 
.
- Si
- Ramas parabólicas:
- Si
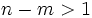, entonces tiene una rama parabólica, tanto por , como por .
- Si
Ejercicio 1 (6'38") Sinopsis: Estudio de las ramas infinitas de la función 
.
Ejercicio 2 (4'38") Sinopsis: Estudio de las ramas infinitas de la función 
.
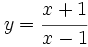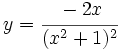Ejercicio 3 (10'44") Sinopsis: Estudio de las ramas infinitas de la función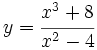 
. (Caso con discontinuidad evitable)
Ejercicios resueltos
Halla todas las ramas infinitas de las siguientes funciones:
- a)
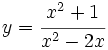b) 
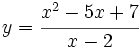c)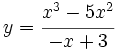 
a) A.V.: x=0, x=2; A.H.: y=1
b) A.V.: x=2; A.O.: y=x-3
c) A.V.: x=3; R.I.
Haz uso de la siguiente escena de Geogebra para comprobar las soluciones:
Representador de funciones Descripción: En esta escena podrás representar funciones definidas en hasta 4 trozos.
