Plantilla:Dominio e imagen de una función (Bachiller)
De Wikipedia
| Revisión de 09:36 4 jun 2017 Coordinador (Discusión | contribuciones) (→Cálculo del dominio y la imagen de una función) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | ==Dominio e imagen de una función== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *Al conjunto de los valores que puede tomar la variable independiente <math>x\;</math>, se le llama '''dominio de definición''' de la función. Lo representaremos por <math>D_f\;</math> ó <math>Dom_f\;</math> | *Al conjunto de los valores que puede tomar la variable independiente <math>x\;</math>, se le llama '''dominio de definición''' de la función. Lo representaremos por <math>D_f\;</math> ó <math>Dom_f\;</math> | ||
| Línea 7: | Línea 6: | ||
| {{geogebra: dominio e imagen de una funcion}} | {{geogebra: dominio e imagen de una funcion}} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_fonemato | + | {{Caja_gris|texto= |
| - | |titulo1=Dominio de definición de una función | + | '''Razones para restringir el dominio de una función:''' |
| - | |duracion=8'51" | + | |
| - | |sinopsis=El "dominio de definición" de la función "f" se denota Dom<sub>f</sub>, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. | + | |
| - | A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Dom<sub>f</sub>, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay. | + | |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/35-dominio-de-definicion-de-una-funcion-3 | + | *Imposibilidad de realizar alguna operación con ciertos valores de <math>x\;</math> que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos). |
| + | *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos). | ||
| + | *Por voluntad de quien propone la función. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | ===Razones para restringir el dominio de una función=== | ||
| - | *Imposibilidad de realizar alguna operación con ciertos valores de <math>x\;</math> (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos) | ||
| - | *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos) | ||
| - | *Por voluntad de quien propone la función. | ||
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| Línea 46: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_julioprofe | + | {{Videotutoriales|titulo=Dominio de una función|enunciado= |
| - | |titulo1=Ejemplo | + | |
| - | |duracion=5'52" | + | |
| - | |sinopsis=Expresa el área de un círculo en función de la longitud de su circunferencia e indica su dominio y recorrido. | + | |
| - | |url1=https://www.youtube.com/watch?v=LVNSEhMdGLk | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ===Reglas fundamentales=== | + | |
| - | En el estudio de una función (dominio, límites, continuidad, etc.) hay una serie de "reglas sagradas" que hay que tener muy presentes: | + | |
| - | {{p}} | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | *Prohibido dividir por cero. | + | |
| - | *Toda raíz de índice par de un número negativo no es un número real. | + | |
| - | *El logaritmo (en cualquier base) de un número no positivo no es un número real. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Reglas "Sagradas" del Cálculo | + | |titulo1=Tutorial |
| - | |duracion=3'43" | + | |duracion=8'51" |
| - | |sinopsis= | + | |sinopsis=El "dominio de definición" de la función "f" se denota Dom<sub>f</sub>, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. |
| - | Hay ciertas reglas en matemáticas que no se pueden violar. Estas reglas afectan a la hora de determinar el dominio de una función. Aquí las vamos a recordar: | + | A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Dom<sub>f</sub>, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay. |
| - | + | ||
| - | *Prohibido dividir por cero. | + | |
| - | *Toda raíz de índice par de un número negativo no es un número real. | + | |
| - | *El logaritmo (en cualquier base) de un número no positivo no es un número real. | + | |
| - | AVISO: será inmisericordemente suspendido ipso facto todo el que viole una Regla Sagrada; caerán sobre él toneladas de desprestigio y deshonor, y el estigma de tan ignominioso acto apestará la honra de su linaje por los siglos de los siglos. | + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/35-dominio-de-definicion-de-una-funcion-3 |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/32-las-reglas-sagradas-del-calculo-5 | + | |
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | ---- |
| - | |titulo1=De las funciones y de las serpientes | + | {{Tabla50|celda1= |
| - | |duracion=9'01" | + | |
| - | |sinopsis=Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas. | + | |
| - | + | ||
| - | En relación a los tres conceptos fundamentales del Cálculo (límite, continuidad y derivada de una función "f" en un punto "c"), y debido a las posibles violaciones de las tres Reglas Sagradas, las funciones son como las serpientes: las hay inofensivas y las hay peligrosas. Por eso, al trabajar con una función "f" en el punto "c", lo primero es invertir un par de segundos en analizar si "f" es o no peligrosa en "c". Naturalmente, si es peligrosa, pondremos todos nuestros sentidos en estado de máxima concentración y alerta, para así intentar evitar que nos mande al otro barrio. | + | |
| - | + | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/33-de-las-funciones-y-las-serpientes | + | |
| - | }} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=9 ejemplos de "serpientes" peligrosas... o no | + | |
| - | |duracion=14'53" | + | |
| - | |sinopsis=En este vídeo vemos ejemplos en los que analizamos la peligrosidad de trabajar (límite, continuidad, derivada) con una cierta función "f" en un cierto punto "c". | + | |
| - | + | ||
| - | Todo se reduce a analizar si en "c" se viola alguna Regla Sagrada; a saber: | + | |
| - | + | ||
| - | *Prohibido dividir por cero. | + | |
| - | *Toda raíz de índice par de un número negativo no es un número real. | + | |
| - | *El logaritmo (en cualquier base) de un número no positivo no es un número real. | + | |
| - | + | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3301-nueve-ejemplos-5 | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ===Signo de una función=== | + | |
| - | El estudio del signo de una función va a ser útil en la representación gráfica de funciones y en el estudio del dominio de funciones. | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=Signo de una función | + | |
| - | |duracion=8'52" | + | |
| - | |sinopsis=A la hora de representar la gráfica de la función "f", el estudio del signo del número real f(x) nos permite conocer la posición de la gráfica respecto al eje de abcisas. | + | |
| - | + | ||
| - | *La gráfica está por encima del eje de abcisas en los puntos "x" tales que f(x) es positivo. | + | |
| - | *La gráfica está por debajo del eje de abcisas en los puntos "x" tales que f(x) es negativo. | + | |
| - | *La gráfica toca al eje de abcisas en los puntos "x" tales que f(x) = 0. | + | |
| - | + | ||
| - | El estudio del signo de una función también es útil cuando queremos determinar el dominio de una función. | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/34-signo-de-una-funcion-4#.WEqb-tLhCM8 | + | |
| - | }} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=Signo de una función (2 ejercicios) | + | |
| - | |duracion=5'45" | + | |
| - | |sinopsis=2 ejercicios sobre el estudio del signo de una función | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3401-dos-ejercicios-4#.WEqd2tLhCM8 | + | |
| - | }} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=Signo de una función (4 ejercicios) | + | |
| - | |duracion=5'45" | + | |
| - | |sinopsis=4 ejercicios sobre el estudio del signo de una función | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3402-cuatro-ejercicios-4#.WEqeQNLhCM8 | + | |
| - | }} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | + | ||
| - | ===Cálculo del dominio y la imagen de una función=== | + | |
| - | {{Videotutoriales|titulo=Cálculo del dominio de una función|enunciado= | + | |
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| |titulo1=1. Ejemplos | |titulo1=1. Ejemplos | ||
| Línea 168: | Línea 86: | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3504-once-ejercicios-4#.WEqaoNLhCM8 | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3504-once-ejercicios-4#.WEqaoNLhCM8 | ||
| }} | }} | ||
| + | |celda2= | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=7. Ejemplos | |titulo1=7. Ejemplos | ||
| Línea 199: | Línea 118: | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=10. Ejemplos | + | |titulo1=12. Ejemplos |
| |duracion=10'03" | |duracion=10'03" | ||
| |sinopsis=7 ejemplos. | |sinopsis=7 ejemplos. | ||
| |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3510-siete-ejercicios-jugando-con-el-coseno-2#.WEqbgNLhCM8 | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/3510-siete-ejercicios-jugando-con-el-coseno-2#.WEqbgNLhCM8 | ||
| + | }} | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=0'48" | ||
| + | |url1=https://www.youtube.com/watch?v=TyioawvW-JA&index=5&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Halla el dominio de <math>f(x)=2x^2+5\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=1'34" | ||
| + | |url1=https://www.youtube.com/watch?v=hDIf2SEQUeI&index=1&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Halla el dominio de <math>n(x)=\cfrac{x^2}{x+2}-5\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=1'11" | ||
| + | |url1=https://www.youtube.com/watch?v=UijSx5DuIpw&index=2&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Halla el dominio de <math>h(x)=\cfrac{3x}{x-5}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=1'14" | ||
| + | |url1=https://www.youtube.com/watch?v=idS3dU_B8lI&index=3&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Halla el dominio de <math>m(x)=\sqrt{2x-6}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=1'02" | ||
| + | |url1=https://www.youtube.com/watch?v=Eqdt_ED2UDk&index=4&list=PL347F4BCD040AB93F | ||
| + | |sinopsis=Halla el dominio de <math>g(x)=\sqrt{x+4}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=1'52" | ||
| + | |url1=https://youtu.be/-9HA_VK3w0M | ||
| + | |sinopsis=Halla el dominio de <math>f(x)=\sqrt{2x-8}\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=7'24" | ||
| + | |url1=https://youtu.be/Y93FyoTSJ1A | ||
| + | |sinopsis=Halla el dominio de: | ||
| + | :a) <math>g(x)=\cfrac{1}{\sqrt{6-\left| x \right|}}\;</math>. | ||
| + | :b) <math>h(x) = \begin{cases} \cfrac{x+10}{(x+10)(x-9)(x-5)} & \mbox{si }x \ne 5 \\ ~ \\ \qquad \qquad \pi & \mbox{si }x=5 \end{cases}</math> | ||
| + | |||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Cálculo del dominio y la imagen de una función|enunciado= | + | {{Videotutoriales|titulo=Dominio e imagen de una función|enunciado= |
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=13´00" | ||
| + | |url1=https://www.youtube.com/watch?v=bqlbWVFZwE8 | ||
| + | |sinopsis=Conceptos de dominio y rango de una función. Ejemplos | ||
| + | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=10'16" | ||
| + | |url1=https://www.youtube.com/watch?v=iKEPhG0xiTY&index=6&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| + | |sinopsis=Tutorial en el que se explica el cálculo del dominio y la imagen de una función dada su gráfica. | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=59'44" | ||
| + | |sinopsis=Dominio y rango de una función. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=glhFLEZgnrE&list=PL3KGq8pH1bFQCtxruKjQqhM4BTwHARnRR&index=8 | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Tutorial 4 | ||
| + | |duracion=11'00" | ||
| + | |sinopsis=Dominio e imagen (o rango) de una función. Ejemplos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=H40lcwlgPMk | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=5'52" | ||
| + | |sinopsis=Expresa el área de un círculo en función de la longitud de su circunferencia e indica su dominio y recorrido. | ||
| + | |url1=https://www.youtube.com/watch?v=LVNSEhMdGLk | ||
| + | }} | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| |titulo1=Funciones polinómicas | |titulo1=Funciones polinómicas | ||
| Línea 213: | Línea 211: | ||
| |url1=https://www.youtube.com/watch?v=QqaU5zXRPKs&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=13 | |url1=https://www.youtube.com/watch?v=QqaU5zXRPKs&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=13 | ||
| }} | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Funciones racionales | ||
| + | |duracion=34'56" | ||
| + | |sinopsis=Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos. | ||
| + | |url1=https://www.youtube.com/watch?v=rv09hXPZ750&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=14 | ||
| }} | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Funciones radicales | ||
| + | |duracion=35'54" | ||
| + | |sinopsis=Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales. | ||
| + | |url1=https://www.youtube.com/watch?v=H4Edt4faBvs&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=15 | ||
| + | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Otras funciones | ||
| + | |duracion=28'14" | ||
| + | |sinopsis=Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales. | ||
| + | |url1=https://www.youtube.com/watch?v=_3zIk2Gq35k&index=16&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Wolfram: Dominio e imagen}} | ||
| + | |||
| + | ==Simetrías de una función== | ||
| + | {{Caja_Amarilla|texto=*Una función es '''par''' si cumple que: <math>f(x)=f(-x) \ , \forall \, x \in Dom_f</math>. En tal caso la gráfica es simétrica respecto del eje Y. | ||
| + | *Una función es '''impar''' si cumple que: <math>f(x)=-f(-x) \ , \forall \, x \in Dom_f</math>. En tal caso la gráfica es simétrica respecto del origen. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Simetrías de una función|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=14'06" | ||
| + | |sinopsis= | ||
| + | *La función "f" se dice "par" si f(-x) = f(x), y se dice "impar" si f(-x) = -f(x). | ||
| + | :*Si "f" es par, su gráfica es simétrica respecto al eje de ordenadas. | ||
| + | :*Si "f" es impar, su gráfica es simétrica respecto al origen de coordenadas. | ||
| + | :*Obvio: si Dom f. no es simétrico respecto al punto "0", la función "f" no es par ni impar. | ||
| + | |||
| + | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real/36-simetrias-de-una-funcion#.WGOfnEZ9U6c | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=34'07" | ||
| + | |sinopsis=Definición de función par e impar. Ejemplos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=uuQGhP-TzPQ | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejemplos | ||
| + | |duracion=19'25" | ||
| + | |sinopsis=Ejemplos de funciones pares e impares. Interpretación gráfica. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=XRLR9iBRTps | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=2'52" | ||
| + | |url1=https://www.youtube.com/watch?v=9_sYOXo94bM&index=1&list=PLBC212040268E63E7 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=2'38" | ||
| + | |url1=https://www.youtube.com/watch?v=aipz-fVm4sk&index=2&list=PLBC212040268E63E7 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=2'20" | ||
| + | |url1=https://www.youtube.com/watch?v=kiH7iBSHzfA&index=3&list=PLBC212040268E63E7 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=2'45" | ||
| + | |url1=https://www.youtube.com/watch?v=3MEIAyCb8IU&index=4&list=PLBC212040268E63E7 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=2'57" | ||
| + | |url1=https://www.youtube.com/watch?v=nZOd68XUqZs&list=PLBC212040268E63E7&index=5 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=3'08" | ||
| + | |url1=https://www.youtube.com/watch?v=NemKDM0bH-c&index=6&list=PLBC212040268E63E7 | ||
| + | |sinopsis=Estudio de las simetrías de una función a partir de su expresión analítica. | ||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
Revisión actual
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 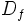 ó
ó 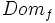
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
 . Lo representaremos por
. Lo representaremos por 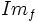 o
o 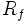 .
.
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
Razones para restringir el dominio de una función:
- Imposibilidad de realizar alguna operación con ciertos valores de
 que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
que incumplan las quie hemos llamdo "reglas sagradas" del Cálculo. (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos, logaritmos de valores no positivos).
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos).
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
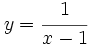
- b)
- c)
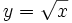
- c)
- d)
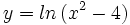
- d)
- e)
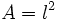 (Área de un cuadrado de lado
(Área de un cuadrado de lado 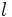 )
)
- e)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
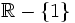 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
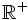 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
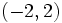 , porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación
, porque el logaritmo de un número sólo existe si éste es positivo. Al resolver la inecuación 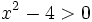 resulta que
resulta que 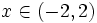 .
.
- d) Su dominio es
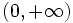 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
El "dominio de definición" de la función "f" se denota Domf, y es el conjunto que forman los números reales "x" que tienen imagen segun "f"; o sea, los "x" tales que al calcular "f(x)" no se viola ninguna Regla Sagrada. A la hora de representar la gráfica de "f" lo primero SIEMPRE es determinar Domf, pues así sabremos en qué puntos del eje de abcisas hay curva y en qué puntos no la hay.
5 ejemplos. Varios ejemplos. 15 ejemplos. 16 ejemplos. 10 ejemplos. 11 ejemplos. | 7 ejemplos. 8 ejemplos. 4 ejemplos. 6 ejemplos. 7 ejemplos. 7 ejemplos. |
Halla el dominio de 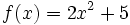 .
.
Halla el dominio de 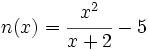 .
.
Halla el dominio de 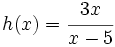 .
.
Halla el dominio de 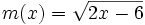 .
.
Halla el dominio de 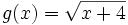 .
.
Halla el dominio de 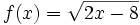 .
.
Halla el dominio de:
- a)
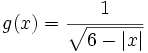 .
.
- b)
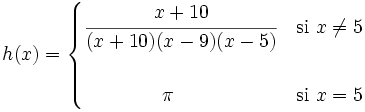
Conceptos de dominio y rango de una función. Ejemplos
Tutorial en el que se explica el cálculo del dominio y la imagen de una función dada su gráfica.
Dominio y rango de una función. Ejemplos.
Dominio e imagen (o rango) de una función. Ejemplos.
Expresa el área de un círculo en función de la longitud de su circunferencia e indica su dominio y recorrido.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales.
|
Actividad: Dominio e imagen de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Simetrías de una función
- Una función es par si cumple que:
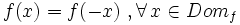 . En tal caso la gráfica es simétrica respecto del eje Y.
. En tal caso la gráfica es simétrica respecto del eje Y.
- Una función es impar si cumple que:
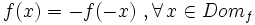 . En tal caso la gráfica es simétrica respecto del origen.
. En tal caso la gráfica es simétrica respecto del origen.
- La función "f" se dice "par" si f(-x) = f(x), y se dice "impar" si f(-x) = -f(x).
- Si "f" es par, su gráfica es simétrica respecto al eje de ordenadas.
- Si "f" es impar, su gráfica es simétrica respecto al origen de coordenadas.
- Obvio: si Dom f. no es simétrico respecto al punto "0", la función "f" no es par ni impar.
Definición de función par e impar. Ejemplos.
Ejemplos de funciones pares e impares. Interpretación gráfica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Estudio de las simetrías de una función a partir de su expresión analítica.
Ejercicios propuestos
|
Ejercicios propuestos: Concepto de función y de dominio de una función |
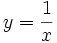 .
.

