Plantilla:Ejercicios y videotutoriales: Tendencias
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:29 12 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace | + | {{Videotutoriales|titulo=Tendencia de una función|enunciado= |
| - | |titulo1=Ejercicio: ''Tendencias'' | + | {{Video_enlace_childtopia |
| + | |titulo1=Ejercicio 1 | ||
| |duracion=1'11" | |duracion=1'11" | ||
| - | |url1=https://www.youtube.com/watch?v=Gcwxtz1A-6U | + | |url1=https://www.youtube.com/watch?v=Gcwxtz1A-6U&index=1&t=11s&list=PLBF1AAC9BD57DFBDE |
| - | |sinopsis=Estudio de las tendencias de una función. | + | |sinopsis=Estudio de las tendencias de una función a partir de su gráfica. |
| }} | }} | ||
| - | {{wolfram desplegable|titulo=Tendencias|contenido= | + | {{Video_enlace_childtopia |
| - | {{wolfram | + | |titulo1=Ejercicio 2 |
| - | |titulo=Actividad: ''Tendencias'' | + | |duracion=1'10" |
| - | |cuerpo= | + | |url1=https://www.youtube.com/watch?v=2aGGIz94V-4&index=2&list=PLBF1AAC9BD57DFBDE |
| - | {{ejercicio_cuerpo | + | |sinopsis=Estudio de las tendencias de una función a partir de su gráfica. |
| - | |enunciado= | + | |
| - | + | ||
| - | + | ||
| - | :a) Averigua la tendencia de la función <math>f(x)=\cfrac{1}{x}\;</math>. cuando <math>x\;</math> se hace infinitamente grande. | + | |
| - | :b) Observa lo que ocurre en el apartado anterior dibujando la función desde x=0 a x=100000. | + | |
| - | + | ||
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) {{consulta|texto=limit x to +oo 1/x}} | + | |
| - | :b) {{consulta|texto=plot 1/x {x,0,100000}}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| }} | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=1'29" | ||
| + | |url1=https://www.youtube.com/watch?v=zHVjfNyLmhU&index=3&t=10s&list=PLBF1AAC9BD57DFBDE | ||
| + | |sinopsis=Estudio de las tendencias de una función a partir de su gráfica. | ||
| }} | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=1'18" | ||
| + | |url1=https://www.youtube.com/watch?v=Ygty8MBN9rg&index=4&t=2s&list=PLBF1AAC9BD57DFBDE | ||
| + | |sinopsis=Estudio de las tendencias de una función a partir de su gráfica. | ||
| }} | }} | ||
| - | {{ejercicio | + | }} |
| + | {{Wolfram: Tendencias de una funcion}} | ||
| + | {{p}} | ||
| + | {{ejemplo | ||
| |titulo=Ejercicio Resuelto: ''Tendencia de una función'' | |titulo=Ejercicio Resuelto: ''Tendencia de una función'' | ||
| - | |cuerpo= | ||
| - | |||
| - | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| '''1. '''Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%. | '''1. '''Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%. | ||
| Línea 82: | Línea 79: | ||
| :g) Es decreciente en todo su dominio. Tiene un máximo en <math>x=0</math> y no tiene mínimos. | :g) Es decreciente en todo su dominio. Tiene un máximo en <math>x=0</math> y no tiene mínimos. | ||
| :h) No es periódica. | :h) No es periódica. | ||
| - | }} | ||
| }} | }} | ||
Revisión actual
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
|
Actividad: Tendencia de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio Resuelto: Tendencia de una función
1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.
- a) Haz una tabla que exprese el precio del coche durante los próximos años.
- b) Representa gráficamente los resultados del apartado a).
- c) Encuentra una fórmula que exprese esta función.
- d) ¿Cómo es la variable independiente: continua o discreta?
- e) ¿Cuál es el dominio de esta función?. ¿Y su imagen?
- f) ¿Cual es la tendencia de esta función segun pasan los años?
- g) Describe el crecimiento e indica si tiene máximos o mínimos.
Solución:
- a) Tabla de valores:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 12.000 | 9.600 | 7.680 | 6.144 | 4.915,2 | 3.932,2 | 3.145,7 | 2.516,6 |
- b) Representación gráfica:
- c) Continua.
- d)
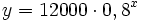 (€)
(€)
- e)
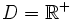 ;
; 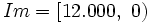 .
.
- f) La función tiende a 0 a medida que transcurre el tiempo.
- g) Es decreciente en todo su dominio. Tiene un máximo en x = 0 y no tiene mínimos.
- h) No es periódica.
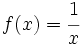 . cuando
. cuando  se hace infinitamente grande.
se hace infinitamente grande.