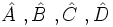Cuadriláteros (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:45 20 jul 2017 Coordinador (Discusión | contribuciones) (→Clasificación de los cuadriláteros) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Clasificación de los cuadriláteros) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| ==Cuadrilátero== | ==Cuadrilátero== | ||
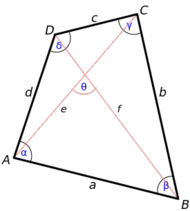
| - | {{Tabla75|celda2=[[Imagen:cuadrilatero.png|center|190px|thumb|'''Cuadrilátero:''' Tiene dos diagonales: ''e'' y ''f''; Sus ángulos suman 360º: α+β+γ+δ=360º.]]|celda1= | + | {{Tabla75|celda2=[[Imagen:cuadrilatero.png|center|190px|thumb|'''Cuadrilátero:''' Tiene dos diagonales (''e'' y ''f'') y sus ángulos suman 360º (α+β+γ+δ=360º).]]|celda1= |
| {{Caja_Amarilla|texto=Un '''cuadrilátero''' es un [[Polígonos (1º ESO)|polígono]] de cuatro [[Polígonos (1º ESO)#Polígono|lados]].}} | {{Caja_Amarilla|texto=Un '''cuadrilátero''' es un [[Polígonos (1º ESO)|polígono]] de cuatro [[Polígonos (1º ESO)#Polígono|lados]].}} | ||
| {{p}} | {{p}} | ||
| Línea 12: | Línea 12: | ||
| '''Nomenclatura:''' | '''Nomenclatura:''' | ||
| *Observa en la figura adjunta cómo se nombran los vértices con letras mayúsculas (A, B, C, D) y los lados con minúsculas (a, b, c, d). Además, aparecen dispuestos de forma consecutiva, siguiendo el sentido contrario de las agujas del reloj. | *Observa en la figura adjunta cómo se nombran los vértices con letras mayúsculas (A, B, C, D) y los lados con minúsculas (a, b, c, d). Además, aparecen dispuestos de forma consecutiva, siguiendo el sentido contrario de las agujas del reloj. | ||
| - | *Para los ángulos se utilizan letras griegas (α, β, γ, δ), pero también se pueden representar por {{sube|porcentaje=20%|contenido=<math>\hat A \ , \hat B \ , \hat C \ , \hat D</math>}} | + | *Para los [[Ángulos (1º ESO)|ángulos]] se utilizan letras griegas (α, β, γ, δ), pero también se pueden representar por {{sube|porcentaje=20%|contenido=<math>\hat A \ , \hat B \ , \hat C \ , \hat D</math>}} |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 20: | Línea 20: | ||
| Todo cuadrilátero cumple las siguientes propiedades: | Todo cuadrilátero cumple las siguientes propiedades: | ||
| - | #Sus cuatro [[ángulos]] suman 360º. | + | #Sus cuatro [[Ángulos (1º ESO)|ángulos]] suman 360º. |
| #Tienen dos diagonales. | #Tienen dos diagonales. | ||
| + | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Ángulos interiores de un cuadrilátero|enunciado= | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejemplos 1 | ||
| + | |duracion=6´48" | ||
| + | |url1=https://www.youtube.com/watch?v=vJskILrx5Kw&list=PLeySRPnY35dEHRD4tjlY_GULJ-MU-8tIx&index=4 | ||
| + | |sinopsis=Ejemplos de aplicación de la propiedad de los cuadriláteros que dice que la suma de sus ángulos es siempre 360º. | ||
| + | }} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=Ejemplos 2 | ||
| + | |duracion=5´23" | ||
| + | |url1=https://www.youtube.com/watch?v=J_g4FuDxzWU&index=5&list=PLeySRPnY35dEHRD4tjlY_GULJ-MU-8tIx | ||
| + | |sinopsis=Ejemplos de aplicación de la propiedad de los cuadriláteros que dice que la suma de sus ángulos es siempre 360º. | ||
| }} | }} | ||
| }} | }} | ||
| Línea 39: | Línea 53: | ||
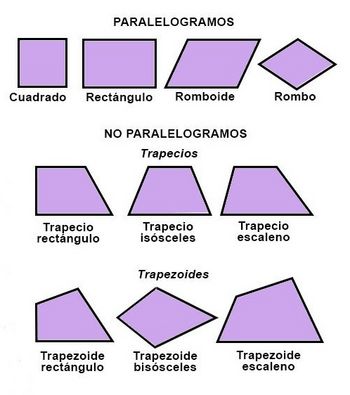
| *'''Paralelogramos:''' tienen lados paralelos dos a dos. | *'''Paralelogramos:''' tienen lados paralelos dos a dos. | ||
| *'''No paralelogramos:''' | *'''No paralelogramos:''' | ||
| - | ** '''Trapecios:''' sólo tienen dos lados paralelos que se llaman '''base mayor''' y '''base menor'''. | + | ** '''Trapecios:''' sólo tienen dos lados paralelos que se llaman '''base mayor''' y '''base menor'''. Se llama '''altura''' a la distancia entre ellos. |
| ** '''Trapezoides:''' sus lados no son paralelos. | ** '''Trapezoides:''' sus lados no son paralelos. | ||
| }} | }} | ||
| Línea 50: | Línea 64: | ||
| * '''Romboides:''' Si tienen sus ángulos opuestos y sus lados opuestos iguales. | * '''Romboides:''' Si tienen sus ángulos opuestos y sus lados opuestos iguales. | ||
| * '''Rombos:''' Si tienen sus cuatro lados iguales y los ángulos opuestos iguales. | * '''Rombos:''' Si tienen sus cuatro lados iguales y los ángulos opuestos iguales. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_masterd | ||
| + | |titulo1=Paralelogramos | ||
| + | |duracion=0´54" | ||
| + | |url1=https://www.youtube.com/watch?v=8EFVgK9JMPE&index=2&list=PL22187EA37AFFD9C3 | ||
| + | |sinopsis=Te explicamos qué es un paralelogramo y los tipos de paralelogramos que existen. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 61: | Línea 82: | ||
| |celda2=[[Imagen:clasificacion_cuadrilateros_2.jpg|center|350px]]}} | |celda2=[[Imagen:clasificacion_cuadrilateros_2.jpg|center|350px]]}} | ||
| {{p}} | {{p}} | ||
| + | {{AI_anaya | ||
| + | |titulo1=Descripción de cuadriláteros | ||
| + | |descripcion= | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/12/04.htm | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/12/04.htm | ||
| + | }} | ||
| {{AI_cidead | {{AI_cidead | ||
| |titulo1=Cuadriláteros: Elementos y clasificación | |titulo1=Cuadriláteros: Elementos y clasificación | ||
| Línea 70: | Línea 104: | ||
| |descripcion=Actividades en las que podrás aprender los distintos tipos de paralelogramos. | |descripcion=Actividades en las que podrás aprender los distintos tipos de paralelogramos. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena9/1quincena9_contenidos_3b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena9/1quincena9_contenidos_3b.htm | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Clasificación de los cuadriláteros|enunciado= | ||
| + | {{Video_enlace_sensei | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=5´45" | ||
| + | |url1=https://youtu.be/ugtxchmVmVo | ||
| + | |sinopsis=Cuadriláteros. Clasificación. | ||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Clasificación de los cuadriláteros | + | |titulo1=Tutorial 2 |
| |duracion=3´01" | |duracion=3´01" | ||
| |url1=https://www.youtube.com/watch?v=tEeSvfvEUu4#t=0m17s | |url1=https://www.youtube.com/watch?v=tEeSvfvEUu4#t=0m17s | ||
| Línea 78: | Línea 119: | ||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Clasificación de los cuadriláteros. Propiedades | + | |titulo1=Tutorial 3 |
| |duracion=2´58" | |duracion=2´58" | ||
| |url1=https://www.youtube.com/watch?v=CUzthyBwR9g | |url1=https://www.youtube.com/watch?v=CUzthyBwR9g | ||
| |sinopsis=Clasificación de los cuadriláteros. Propiedades. | |sinopsis=Clasificación de los cuadriláteros. Propiedades. | ||
| }} | }} | ||
| + | }}{{Video_enlace_profealex | ||
| + | |titulo1=Trapecios: clasificación y características | ||
| + | |duracion=4´54" | ||
| + | |url1=https://www.youtube.com/watch?v=nza1v76bXSk&list=PLeySRPnY35dEHRD4tjlY_GULJ-MU-8tIx&index=3 | ||
| + | |sinopsis=Los trapecios, su clasificación y sus características. | ||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| - | ==Diagonales de los paralelogramos== | + | ==Propiedades de los paralelogramos== |
| + | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| + | |||
| + | *Los lados opuestos tienen la misma longitud. | ||
| + | *Los ángulos opuestos son iguales. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Diagonales de los paralelogramos=== | ||
| {{Tabla75|celda2=[[Imagen:diag_paralelogramos.jpg|center|350px]] | {{Tabla75|celda2=[[Imagen:diag_paralelogramos.jpg|center|350px]] | ||
| |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= | |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| Línea 95: | Línea 150: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Ejes de simetría de los paralelogramos== | + | |
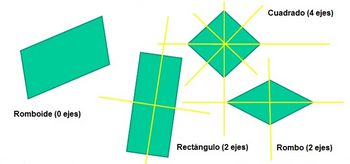
| + | ===Ejes de simetría de los paralelogramos=== | ||
| {{Tabla75|celda2=[[Imagen:simetrias_paralelogramos.jpg|center|350px]] | {{Tabla75|celda2=[[Imagen:simetrias_paralelogramos.jpg|center|350px]] | ||
| |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= | |celda1={{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| Línea 147: | Línea 203: | ||
| |url1=https://www.youtube.com/watch?v=X9rRuGYdzmo | |url1=https://www.youtube.com/watch?v=X9rRuGYdzmo | ||
| |sinopsis=Construcción de un trapecio conocidos sus lados, con regla y compás. | |sinopsis=Construcción de un trapecio conocidos sus lados, con regla y compás. | ||
| + | }} | ||
| + | |||
| + | ==Actividades== | ||
| + | {{AI_descartes | ||
| + | |titulo1=Los cuadriláteros: tipos y características | ||
| + | |descripcion=Actividades sobre cuadriláteros, paralelogramos, trapecios y cometas. | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/Los_cuadrilateros/Cuadrilateros1.htm | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |descripcion=Ejercicios de autoevaluación sobre cuadriláteros. | ||
| + | |url1=https://www.vitutor.com/geo/eso/pl_6e.html | ||
| + | |titulo1=Autoevaluación: ''Cuadriláteros'' | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
[editar]
Cuadrilátero
|
Nomenclatura:
 Propiedades Todo cuadrilátero cumple las siguientes propiedades:
|  |
Ejemplos 1 (6´48") Sinopsis: Ejemplos de aplicación de la propiedad de los cuadriláteros que dice que la suma de sus ángulos es siempre 360º.
Ejemplos 2 (5´23") Sinopsis: Ejemplos de aplicación de la propiedad de los cuadriláteros que dice que la suma de sus ángulos es siempre 360º.
Increíbles cuadriláteros (1´54") Sinopsis: Los cuadriláteros son figuras planas bastante interesantes. Comenzaremos con este pequeño video mostrando una de sus propiedades.
[editar]
Clasificación de los cuadriláteros
Los cuadriláteros se clasifican, atendiendo al paralelismo de sus lados, en:
Los paralelogramos se clasifican, atendiendo a sus lados y a sus ángulos, en:
 Paralelogramos (0´54") Sinopsis:Te explicamos qué es un paralelogramo y los tipos de paralelogramos que existen. Los trapecios se clasifican en:
|  |
Descripción de cuadriláteros Descripción: 
Cuadriláteros: Elementos y clasificación Descripción: Actividades en las que podrás aprender el concepto de cuadrilátero, identificar sus elementos y clasificar los cuadriláteros atendiendo al número de lados paralelos que poseen.
Clasificación de los paralelogramos Descripción: Actividades en las que podrás aprender los distintos tipos de paralelogramos.
Tutorial 1 (5´45") Sinopsis:Cuadriláteros. Clasificación.
Tutorial 2 (3´01") Sinopsis:Este vídeo aborda la clasificación de cuadriláteros y paralelogramos.
Tutorial 3 (2´58") Sinopsis:Clasificación de los cuadriláteros. Propiedades.
Trapecios: clasificación y características (4´54") Sinopsis: Los trapecios, su clasificación y sus características.
[editar]
Propiedades de los paralelogramos
Propiedades
- Los lados opuestos tienen la misma longitud.
- Los ángulos opuestos son iguales.
[editar]
Diagonales de los paralelogramos
Propiedades
|  |
[editar]
Ejes de simetría de los paralelogramos
Propiedades
|  |
[editar]
Construcciones con regla y compás
Cuadrado conocido su lado (1´21") Sinopsis: Construcción de un cuadrado conocido el lado, con regla y compás.
Rectángulo conocidos sus dos lados (4´23") Sinopsis: Construcción de un rectángulo conocidos sus lados, con regla y compás.
Rombo conocidas sus dos diagonales (4´36") Sinopsis: Construcción de un rombo conocidas sus diagonales, con regla y compás.
Romboide conocidos sus dos lados y la altura (2´21") Sinopsis: Construcción de un romboide conocidos dos lados y la altura, con regla y compás.
Romboide conocidos sus dos lados y una diagonal (3´37") Sinopsis: Construcción de un romboide conocidos sus dos lados y una diagonal, con regla y compás.
Romboide conocidos sus dos lados y un ángulo (4´01") Sinopsis: Construcción de un romboide conocidos sus dos lados y un ángulo, con regla y compás.
Trapecio conocidos sus cuatro lados (3´53") Sinopsis: Construcción de un trapecio conocidos sus lados, con regla y compás.
[editar]
Actividades
Los cuadriláteros: tipos y características Descripción: Actividades sobre cuadriláteros, paralelogramos, trapecios y cometas.
Autoevaluación: Cuadriláteros Descripción: Ejercicios de autoevaluación sobre cuadriláteros.
