Cuerpos geométricos (1º ESO)
De Wikipedia
| Revisión de 07:29 15 oct 2017 Coordinador (Discusión | contribuciones) (→Actividades sobre cuerpos redondos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Cuerpos de revolución) |
||
| Línea 16: | Línea 16: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| =Cuerpos geométricos= | =Cuerpos geométricos= | ||
| {{Tabla75|celda2=[[Imagen:cuerpos_geo.jpg|200px|center]]|celda1= | {{Tabla75|celda2=[[Imagen:cuerpos_geo.jpg|200px|center]]|celda1= | ||
| Línea 24: | Línea 25: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *'''Poliedros:''' son cuerpos geométricos cerrados, limitados por caras poligonales. | *'''Poliedros:''' son cuerpos geométricos cerrados, limitados por caras poligonales. | ||
| - | + | *'''Cuerpos redondos:''' son cuerpos geométricos limitados total o parcialmente por superficies curvas. Dentro de éstos están los '''cuerpos de revolución''', que son cuerpos redondos que se obtienen al girar una figura plana alrededor de un eje. | |
| - | *'''Cuerpos de revolución:''' son cuerpos que se obtienen al girar una figura plana alrededor de un eje. | + | |
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Cuerpos geométricos|enunciado= | ||
| + | {{Video_enlace_angelmartinez | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=0'42" | ||
| + | |sinopsis=Cuerpos geométricos: poliedros y cuerpos redondos. | ||
| + | |url1=https://www.youtube.com/watch?v=Z1iFqeHGU_o | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=5'09" | ||
| + | |sinopsis=Este video resume gran parte de lo que se va a ver en este tema: | ||
| + | *Poliedros y cuerpos redondos. | ||
| + | *Poliedros: Elementos y clasificación. | ||
| + | *Prismas: elementos y clasificación. | ||
| + | *Pirámides: elementos y clasificación. | ||
| + | *Poliedros regulares. | ||
| + | *Cuerpos redondos: cilindro, cono y esfera. | ||
| + | |url1=https://www.youtube.com/watch?v=lqv0dYnKTxA | ||
| + | }} | ||
| + | ---- | ||
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| |titulo1=Ejercicio | |titulo1=Ejercicio | ||
| Línea 34: | Línea 54: | ||
| |sinopsis=Dibuja un cuerpo geométrico cuya base sea una circunferencia y explica razonadamente si es un poliedro. | |sinopsis=Dibuja un cuerpo geométrico cuya base sea una circunferencia y explica razonadamente si es un poliedro. | ||
| |url1=https://www.youtube.com/watch?v=S84BU6zpqa8 | |url1=https://www.youtube.com/watch?v=S84BU6zpqa8 | ||
| + | }} | ||
| + | }} | ||
| + | {{AI_enlace | ||
| + | |titulo1=¿Poliedro o cuerpo redondo? | ||
| + | |descripcion=Actividad en la que podrás aprender a distinguir entre poliedros y cuerpos redondos. | ||
| + | |url1=http://www.juntadeandalucia.es/averroes/centros-tic/41009470/helvia/aula/archivos/repositorio/0/193/html/recursos/la/U14/pages/recursos/143304_P198/es_carcasa.html | ||
| }} | }} | ||
| Línea 73: | Línea 99: | ||
| |url1=http://maralboran.org/web_ma/descartes/1y2_eso/redondos/revoluc.htm | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/redondos/revoluc.htm | ||
| }} | }} | ||
| - | {{Actividades|titulo=Autoevaluación: ''Cuerpos de revolución''|enunciado= | + | |
| - | {{AI_enlace | + | |
| - | |titulo1=Actividad 1 | + | |
| - | |descripcion=Une las figuras de la derecha con el cuerpo geométrico que se obtiene al hacerlas girar. | + | |
| - | |url1=http://www.ceipgrancapitan.es/matematicas/contenidos_mat/poliedros/redondos_1.htm | + | |
| - | }} | + | |
| - | {{AI_enlace | + | |
| - | |titulo1=Actividad 2 | + | |
| - | |descripcion=Une las figuras de la derecha con el cuerpo geométrico que se obtiene al hacerlas girar. | + | |
| - | |url1=http://www.ceipgrancapitan.es/matematicas/contenidos_mat/poliedros/redondos_2.htm | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ==Cilindro== | ==Cilindro== | ||
| Línea 108: | Línea 123: | ||
| ==Esfera== | ==Esfera== | ||
| {{Definición de esfera}} | {{Definición de esfera}} | ||
| - | |||
| - | |||
| =Actividades sobre cuerpos geométricos= | =Actividades sobre cuerpos geométricos= | ||
| - | {{AI_descartes | + | {{AI cuerpos geométricos 1ESO}} |
| - | |titulo1=Cuerpos geométricos | + | |
| - | |descripcion=Descripción y propiedades características de los cuerpos geométricos elementales. | + | |
| - | + | ||
| - | '''Objetivos:''' | + | |
| - | + | ||
| - | *Distinguir los diferentes tipos de sólidos que hay. | + | |
| - | *Utilizar correctamente los nombres de los diferentes sólidos. | + | |
| - | *Utilizar correctamente los nombres para referirse a las partes de un cuerpo sólido. | + | |
| - | *Saber las propiedades que caracteriza a un sólido. | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/Cuerpos_d3/index.htm | + | |
| - | }} | + | |
| - | {{AI_descartes | + | |
| - | |titulo1=Los poliedros regulares y la esfera | + | |
| - | |descripcion='''Objetivos:''' | + | |
| - | + | ||
| - | *Distinguir los poliedros regulares y reconocer sus propiedades más significativas. | + | |
| - | *Relacionar las propiedades de la esfera con las de los poliedros regulares. | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/Poliedros_regulares_d3/index.htm | + | |
| - | }} | + | |
| - | {{AI_enlace | + | |
| - | |titulo1=Autoevaluación: ''Cuerpos geométricos'' | + | |
| - | |descripcion=Repasa todo lo visto en este tema en 42 actividades interactivas. | + | |
| - | |url1=http://cplosangeles.educarex.es/web/edilim/tercer_ciclo/matematicas6/cuerpos_geometricos_6/cuerpos_geometricos_6.html | + | |
| - | }} | + | |
| - | + | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Un toque divertido para empezar el tema:
Troncho y Poncho quedan atrapados en un mundo tridimensional donde aprenderán las áreas y volúmenes de los poliedros más sencillos.
Cuerpos geométricos
Un cuerpo geométrico es una figura geométrica de tres dimensiones. Tiene largo, ancho y alto. Los cuerpos geométricos se clasifican en:
|
Cuerpos geométricos: poliedros y cuerpos redondos.
Este video resume gran parte de lo que se va a ver en este tema:
- Poliedros y cuerpos redondos.
- Poliedros: Elementos y clasificación.
- Prismas: elementos y clasificación.
- Pirámides: elementos y clasificación.
- Poliedros regulares.
- Cuerpos redondos: cilindro, cono y esfera.
Dibuja un cuerpo geométrico cuya base sea una circunferencia y explica razonadamente si es un poliedro.
Actividad en la que podrás aprender a distinguir entre poliedros y cuerpos redondos.
Poliedros
| El siguiente videotutorial resume los conceptos y resultados más importantes del tema:
Videotutorial que resume los conceptos y resultados más importantes del tema:
[editar] Definición de poliedroPoliedro es un cuerpo geométrico cerrado, limitado por caras poligonales. Las caras de un poliedro, al ser polígonos, no pueden ser curvas. Así, un cono, una esfera o un cilindro, no son poliedros. Definición de poliedro. Ejemplos. Actividades en la que podrás aprender lo que es un poliedro. |
Elementos de un poliedro
- Caras: Polígonos que limitan al poliedro.
- Aristas: Segmentos intersección de las caras.
- Vértices: Puntos de intersección de las aristas.
Se llama orden de un vértice de un poliedro, al número de caras (o aristas) que concurren en él.
Definición de poliedro. Elementos.
Definición de poliedro. Elementos.
Actividad en la que deberás separar los cuerpos que son poliedros de los que no lo son.
Actividades en la que podrás estudiar los distintos elementos de un poliedro.
Definición de poliedro. Elementos. Relación de Euler.
Denominación de los poliedros
Los poliedros son denominados de acuerdo a su número de caras. Su designación se basa en el griego clásico.
| Nombre | Nº caras | Nombre | Nº caras | Nombre | Nº caras |
|---|---|---|---|---|---|
| tetraedro | 4 | tridecaedro | 13 | tetracontaedro | 40 |
| pentaedro | 5 | tetradecaedro | 14 | pentacontaedro | 50 |
| hexaedro | 6 | pentadecaedro | 15 | hexacontaedro | 60 |
| heptaedro | 7 | hexadecaedro | 16 | heptacontaedro | 70 |
| octaedro | 8 | heptadecaedro | 17 | octacontaedro | 80 |
| eneaedro | 9 | octadecaedro | 18 | eneacontaedro | 90 |
| decaedro | 10 | eneadecaedro | 19 | hectaedro | 100 |
| endecaedro | 11 | icosaedro | 20 | chiliedro | 1000 |
| dodecaedro | 12 | triacontaedro | 30 | miriedro | 10000 |
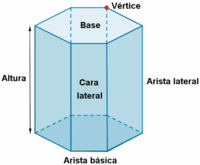
Prisma
Prisma: definición y elementos. Actividad en la que se presentan distintos tipos de prismas y en la que podrás ver sus elementos. | Elementos de un prisma
de http://calculo.cc |
Clasificación de los prismas
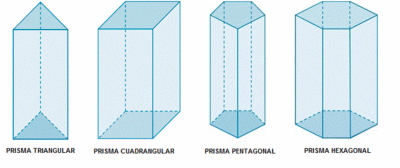
- Atendiendo a sus bases: En función del polígono de las bases, los prismas pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.
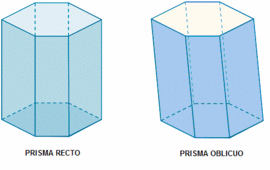
- Atendiendo a su inclinación: Si las caras laterales son perpendicualres a las bases (son rectángulos), el prisma es recto, si no , es oblicuo.
- Atendiendo a su regularidad: Un prisma es regular si su base es un polígono regular. En caso contrario es irregular. En una prisma regular, todas las aristas laterales son iguales y las caras laterales son rectángulos iguales
Clasificación de los prismas.
Dibuja un prisma de base pentagonal y recuenta sus caras, vértices y aristas.
Actividad en la que se presentan distintos tipos de prismas regulares.
Actividad interactiva en la que aprenderás los elementos y la clasificación de los prismas regulares.
Atendiendo a su inclinación
de http://calculo.cc | Atendiendo a su base
de http://calculo.cc |
Paralelepípedos
- Los paralelepípedos son prismas en los que todas sus caras son paralelogramos.
- Las bases han de ser paralelogramos y por tanto los paralelepípedos son prismas cuadrangulares.
- Entre ellos destacamos cuatro en particular:
- Ortoedro: sus caras son rectángulos.
- Cubo: sus caras son cuadrados.
- Romboedro: Todas sus caras son rombos.
- Romboiedro: Todas sus caras son romboides.
Actividad en la que podrás conocer los paralelepípedos y sus distintos tipos.
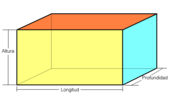
Ortoedro
| Ortoedro
|
Desarrollo plano de un prisma
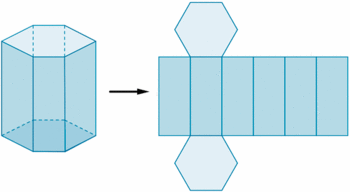
Si representamos en un plano todas las caras de un prisma, de forma contigua, obtenemos lo que se denomina desarrollo plano del prisma.
Fíjate en el siguiente prisma hexagonal. Si cortásemos adecuadamente el prisma, siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura.
de http://calculo.cc
Actividad en la que se presentan los desarrollos planos de distintos prismas rectos regulares.
Dibuja el desarrollo plano del siguiente poliedro.
Actividades
Ejecicios de autoevaluación sobre los prismas.
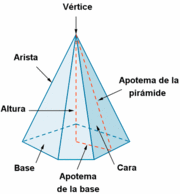
Pirámide
Actividad en la que se presenta la pirámide y sus elementos. Pirámide: definición y elementos. | Piramide recta
|
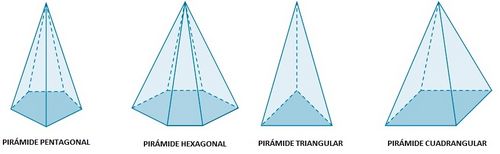
Clasificación de las pirámides
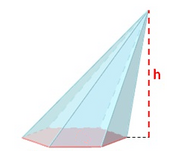
| Pirámide oblicua
de http://universoformulas.com |
Clasificación de las pirámides. Actividad en la que se presentan distintos tipos de pirámides regulares. Clasificación de las pirámides atendiendo a su base
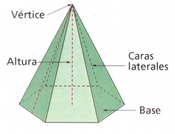
de http://calculo.cc En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. Definiciones, elementos y propiedades. | Elementos de una pirámide regular
de http://calculo.cc |
Dibuja un pirámide de base cuadrangular regular y una pirámide de base triangular irregulr. Recuenta sus caras, vértices y aristas.
Ejecicios de autoevaluación sobre la pirámide.
Desarrollo plano de una pirámide
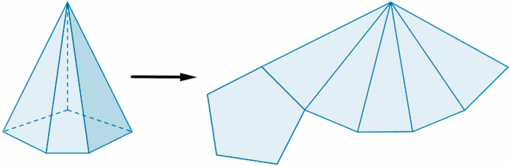
Si representamos en un plano todas las caras de una pirámide, de forma contigua, obtenemos lo que se denomina desarrollo plano de la pirámide.
Fíjate en la siguiente pirámide pentagonal. Si la cortásemos adecuadamente, siguiendo ciertas aristas, podríamos desplegarla como se muestra en la siguiente figura.
de http://calculo.cc
Actividad en la que podrás ver el desarrollo plano de distintas pirámides rectas regulares.
Dibuja el desarrollo plano del siguiente poliedro.
Poliedros regulares
- Poliedro regular es aquel que cumple:
- Sus caras son polígonos regulares iguales.
- Todos los vértices tienen el mismo orden (en todos ellos concurren el mismo número de aristas).
- Sólo hay cinco poliedros regulares, los llamados sólidos platónicos: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
Videotutorial.
Videotutorial.
Videotutorial.
El tetraedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El hexaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El octaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
Calcula el área de un dodecaedro de 6 cm de arista y 4 cm de radio.
En esta escena podrás ver y rotar los poliedros regulares.
Actividad en la que se presentan los 5 poliedros regulares y se hace un recuento de sus elementos.
Actividad interactiva sobre poliedros regulares.
Actividades sobre el tetraedro.
Actividades sobre el octaaedro.
Actividades sobre el hexaedro o cubo.
Actividades sobre el dodecaedro.
Ejecicios de autoevaluación sobre poliedros regulares.
Desarrollo plano de los poliedros regulares
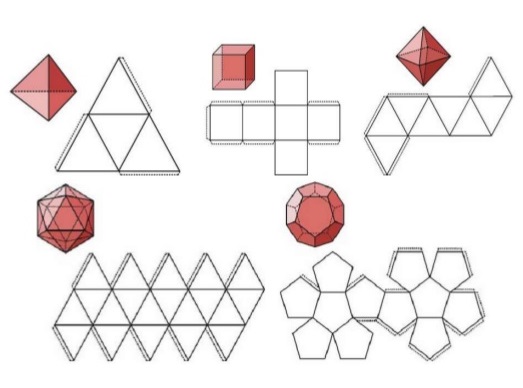
Si representamos en un plano todas las caras de un poliedro, de forma contigua, obtenemos lo que se denomina desarrollo plano del poliedro.
Si cortásemos adecuadamente cada uno de los poliedros regulares, siguiendo ciertas aristas, podríamos desplegarlos como se muestra en la imagen adjunta.
Actividad en la que se muestra el desarrollo plano de los 5 poliedros regulares.
Recursos
{{{descripcion}}}
{{{descripcion}}}
{{{descripcion}}}
{{{descripcion}}}
Actividades
Actividades sobre los elementos de prismas y pirámides.
Cuerpos de revolución
Los cuerpos de revolución son aquellos que se obtienen al girar una figura plana alrededor de un eje.
Entre ellos cabe destacar el cilindro, el cono y la esfera, que pasamos a estudiar con detalle.
Videotutorial que habla de los cuerpos de revolución: cilindro, cono y esfera.
Un cuerpo de revolución se genera cuando hacemos girar un polígono sobre un eje imaginario. Así, obtenemos figuras como el cilindro, el cono o la esferta.
Actividades sobre los cuerpos de revolución más conocidos: el cono, el cilindro y la esfera.
Cilindro
Un cilindro es un cuerpo de revolución que se obtiene haciendo girar un rectángulo alrededor de uno de sus lados. Elementos del cilindro:
|
Actividades en la que podrás ver cómo se genera un cilindro y estudiar sus elementos.
Definición y elementos del cilindro.
Desarrollo plano del cilindro
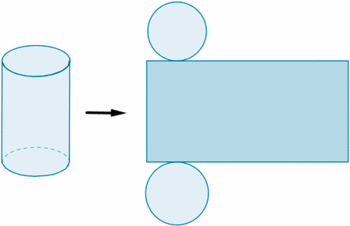
Si representamos en un plano los distintos elementos de la superficie de un cilindro, de forma contigua, obtenemos lo que se denomina desarrollo plano del cilindro.
Si cortásemos adecuadamente un cilindro, podríamos desplegarlos como se muestra en la siguiente imagen.
de http://calculo.cc
Actividades en la que podrás ver cómo es el desarrollo plano de un cilindro recto.
Dibuja el desarrollo plano de un cilindro de 2cm de radio y 5 cm de altura.
Cono
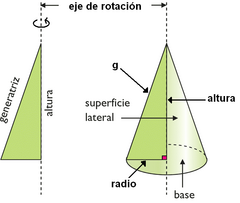
Un cono es un cuerpo de revolución que se obtiene haciendo girar un triángulo rectángulo alrededor de uno de sus catetos. Elementos del cono:
|
Actividades en la que podrás ver cómo se genera un cono y estudiar sus elementos.
Definición y elementos del cono.
Elementos del cono.
Calcula la altura de un cono cuya generatriz mide 10 cm y cuyo radio de la base es de 6 cm.
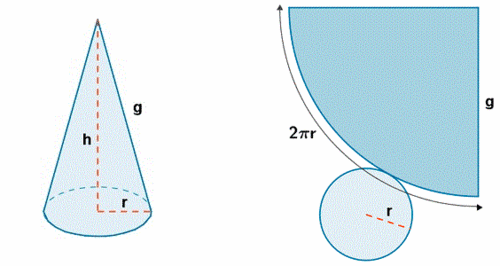
Desarrollo plano del cono
Si representamos en un plano los distintos elementos de la superficie de un cono, de forma contigua, obtenemos lo que se denomina desarrollo plano del cono.
Si cortásemos adecuadamente un cono, podríamos desplegarlos como se muestra en la siguiente imagen.
de http://calculo.cc
Actividades en la que podrás ver cómo es el desarrollo plano de un cono recto.
Dibuja el cono de revolución y su desarrollo plano sabiendo que el radio de la base es 3 cm y su generatriz, 6 cm.
Actividades
Ejecicios de autoevaluación sobre el cilindro y el cono.
Esfera
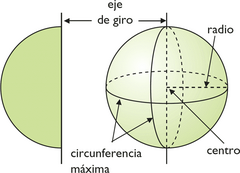
Una esfera es un cuerpo de revolución que se obtiene haciendo girar un semicírculo alrededor de su diámetro. Elementos de la esfera:
|
Actividades en la que podrás ver cómo se genera una esfera y estudiar sus elementos.
Actividades sobre cuerpos geométricos
Descripción y propiedades características de los cuerpos geométricos elementales.
Objetivos:
- Distinguir los diferentes tipos de sólidos que hay.
- Utilizar correctamente los nombres de los diferentes sólidos.
- Utilizar correctamente los nombres para referirse a las partes de un cuerpo sólido.
- Saber las propiedades que caracteriza a un sólido.
Objetivos:
- Distinguir los poliedros regulares y reconocer sus propiedades más significativas.
- Relacionar las propiedades de la esfera con las de los poliedros regulares.
Repasa todo lo visto en este tema en 42 actividades interactivas.
Actividad de autoevaluación sobre cuerpos redondos.
Actividad de autoevaluación sobre cuerpos geométricos.