Plantilla:Proporcionalidad compuesta
De Wikipedia
| Revisión de 12:47 21 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto=Cuando se trabaja con más de dos magnitudes ligadas por la relación de proporcionalidad (directa y/o inversa) diremos que nos encontramos frente a una situación de '''proporcionalidad compuesta'''.}} | {{Caja_Amarilla|texto=Cuando se trabaja con más de dos magnitudes ligadas por la relación de proporcionalidad (directa y/o inversa) diremos que nos encontramos frente a una situación de '''proporcionalidad compuesta'''.}} | ||
| + | {{p}} | ||
| + | {{AI_melide | ||
| + | |titulo1=Ejemplos | ||
| + | |descripcion=Ejemplos sobre proporcionalidad compuesta. | ||
| + | |url1=http://maralboran.org/web_ma/Melide/Razon_y_proporcion/Proporcionalidad%20compuesta.html | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| Línea 7: | Línea 13: | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| + | '''Método rápido:''' | ||
| + | |||
| {{Tabla50|celda1= | {{Tabla50|celda1= | ||
| Tenemos tres variables: Superficie, número de días y numero de horas diarias. | Tenemos tres variables: Superficie, número de días y numero de horas diarias. | ||
| Línea 14: | Línea 22: | ||
| Si fijamos el número de días, a mayor '''superficie''', mayor '''número de horas de trabajo diarias''': La proporcionalidad es directa. | Si fijamos el número de días, a mayor '''superficie''', mayor '''número de horas de trabajo diarias''': La proporcionalidad es directa. | ||
| - | Superficie Nº de días Nº horas diarias | + | Superficie (m<sup>2</sup>) Nº de días Nº horas diarias |
| - | ---------- ---------- I ---------------- | + | -------------- ----------- I ----------------- |
| 260 ------> 5 ------> 8 | 260 ------> 5 ------> 8 | ||
| 500 ------> 7 ------> x | 500 ------> 7 ------> x | ||
| Línea 23: | Línea 31: | ||
| |celda2= | |celda2= | ||
| - | <center><math>\cfrac{260}{500} \cdot \cfrac{7}{5} = \cfrac{8}{x}</math></center> | + | {{b4}}{{b4}}{{b4}}{{b4}}<math>\cfrac{260}{500} \cdot \cfrac{7}{5} = \cfrac{8}{x}</math> |
| - | {{b4}} | + | {{p}} |
| - | {{b4}} | + | <br> |
| - | <center><math> x = \cfrac{500 \cdot 5 \cdot 8}{260 \cdot 7} = 10.989... </math></center> | + | {{p}} |
| - | {{b4}} | + | {{b4}}{{b4}}{{b4}}{{b4}}<math> x = \cfrac{500 \cdot 5 \cdot 8}{260 \cdot 7} = 10.989... </math> |
| - | <center><math> x \approx 11</math> horas diarias</center> | + | {{p}} |
| + | <br> | ||
| + | {{p}} | ||
| + | {{b4}}{{b4}}{{b4}}{{b4}}<math> x \approx 11</math> {{b}}horas diarias. | ||
| + | |||
| + | }} | ||
| + | ---- | ||
| + | '''Método paso a paso:''' | ||
| + | {{Tabla50|celda1= | ||
| + | Fijo la superficie en 260 m<sup>2</sup>: | ||
| + | |||
| + | Superficie (m<sup>2</sup>) Nº de días Nº horas diarias | ||
| + | -------------- ----------- I ----------------- | ||
| + | 260 ------> 5 ------> 8 | ||
| + | 260 ------> 7 ------> y | ||
| + | |||
| + | |celda2= | ||
| + | |||
| + | {{b4}}{{b4}}{{b4}}{{b4}}<math>y= \cfrac{5 \cdot 8}{7}=\cfrac{40}{7}</math> {{b}}días. | ||
| + | |||
| + | }} | ||
| + | {{Tabla50|celda1= | ||
| + | Fijo los días en 7: | ||
| + | |||
| + | Superficie (m<sup>2</sup>) Nº de días Nº horas diarias | ||
| + | -------------- ----------- I ----------------- | ||
| + | 260 ------> 7 ------> 40/7 | ||
| + | 500 ------> 7 ------> x | ||
| + | └---------------------------------------┘ | ||
| + | D | ||
| + | |celda2= | ||
| + | |||
| + | {{b4}}{{b4}}{{b4}}{{b4}}<math>x= 500 \cdot \cfrac{40}{7} : 260=</math> | ||
| + | |||
| + | {{b4}}{{b4}}{{b4}}{{b4}}{{b4}}{{b}}<math>=\cfrac{500 \cdot 40}{7 \cdot 260} = 10.989... \approx 11</math> {{b}}horas diarias. | ||
| }} | }} | ||
| Línea 37: | Línea 79: | ||
| {{Videotutoriales|titulo=Proporcionalidad compuesta|enunciado= | {{Videotutoriales|titulo=Proporcionalidad compuesta|enunciado= | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Tutorial | + | |titulo1=Tutorial 1 |
| |duracion=25'33" | |duracion=25'33" | ||
| |sinopsis=Tutorial que explica los problemas de proporcionalidad compuesta (directa e inversa), viendo distintos métodos para dar con la solución. | |sinopsis=Tutorial que explica los problemas de proporcionalidad compuesta (directa e inversa), viendo distintos métodos para dar con la solución. | ||
| |url1=https://www.youtube.com/watch?v=wFhaV73mrpA&index=6&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa | |url1=https://www.youtube.com/watch?v=wFhaV73mrpA&index=6&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2a | ||
| + | |duracion=5'56" | ||
| + | |sinopsis=Tutorial que explica los problemas de proporcionalidad compuesta. | ||
| + | |url1=https://youtu.be/ciO1tG_PDV0?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2b | ||
| + | |duracion=8'27" | ||
| + | |sinopsis=Ejemplos de problemas de proporcionalidad compuesta. | ||
| + | |url1=https://youtu.be/R27Xqw-TrMk?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2c | ||
| + | |duracion=6'21" | ||
| + | |sinopsis=Tutorial que explica los problemas de proporcionalidad compuesta por reducción a la unidad. | ||
| + | |url1=https://youtu.be/-pRQ_vm3s5o?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2d | ||
| + | |duracion=6'32" | ||
| + | |sinopsis=Ejemplos de problemas de proporcionalidad compuesta por reducción a la unidad. | ||
| + | |url1=https://youtu.be/7s90NSQ2ESE?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| }} | }} | ||
| ---- | ---- | ||
Revisión actual
Cuando se trabaja con más de dos magnitudes ligadas por la relación de proporcionalidad (directa y/o inversa) diremos que nos encontramos frente a una situación de proporcionalidad compuesta.
Ejemplos sobre proporcionalidad compuesta.
Ejercicio resuelto: Proporcionalidad compuesta
Un solador embaldosa 260 m2 de suelo en 5 días trabajando 8 horas diarias. Se compromete a embaldosar un suelo de 500 m2 en 7 días. ¿Cuántas horas diarias tiene que trabajar?
Método rápido:
| Tenemos tres variables: Superficie, número de días y numero de horas diarias.
Si fijamos la superficie, a máyor número de días, menor número de horas de trabajo diarias: La proporcionalidad es inversa. Si fijamos el número de días, a mayor superficie, mayor número de horas de trabajo diarias: La proporcionalidad es directa. Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 5 ------> 8
500 ------> 7 ------> x
└---------------------------------------┘
D
| 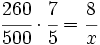
|
Método paso a paso:
Fijo la superficie en 260 m2:
Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 5 ------> 8
260 ------> 7 ------> y
| 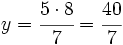 días. días.
|
Fijo los días en 7:
Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 7 ------> 40/7
500 ------> 7 ------> x
└---------------------------------------┘
D
| 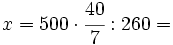
|
Tutorial que explica los problemas de proporcionalidad compuesta (directa e inversa), viendo distintos métodos para dar con la solución.
Tutorial que explica los problemas de proporcionalidad compuesta.
Ejemplos de problemas de proporcionalidad compuesta.
Tutorial que explica los problemas de proporcionalidad compuesta por reducción a la unidad.
Ejemplos de problemas de proporcionalidad compuesta por reducción a la unidad.
Para cortar el césped de un campo de futbol de 4500 m2 precisamos 3 operarios trabajando durante hora y media. ¿Cuántos operarios precisaremos otro día si queremos cortar el césped de otro campo de 6000 m2 y contamos con 2 horas para hacer el trabajo?
Problema.
Practica con distintas situaciones de proporcionalidad compuesta.
Practica con problemas de proporcionalidad compuesta de varios tipos.
Problemas de autoevaluación sobre proporcionalidad compuesta.
Problemas de autoevaluación sobre proporcionalidad compuesta.
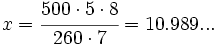
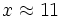 horas diarias.
horas diarias.
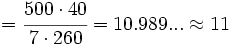 horas diarias.
horas diarias.

