Polígonos regulares (1º ESO)
De Wikipedia
| Revisión de 07:10 22 jul 2017 Coordinador (Discusión | contribuciones) (→Medida de los ángulos de un polígono regular) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Medida de los ángulos de un polígono regular) |
||
| Línea 7: | Línea 7: | ||
| ==Polígono regular== | ==Polígono regular== | ||
| {{Caja_Amarilla|texto=Un '''polígono regular''' es aquel cuyos lados tienen la misma longitud y cuyos ángulos son iguales.}} | {{Caja_Amarilla|texto=Un '''polígono regular''' es aquel cuyos lados tienen la misma longitud y cuyos ángulos son iguales.}} | ||
| + | {{p}} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Polígono regular | ||
| + | |descripcion=Actividad sobre polígonos regulares. | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/Poligonos_regulares_y_circulos/Polici1.htm | ||
| + | }} | ||
| {{p}} | {{p}} | ||
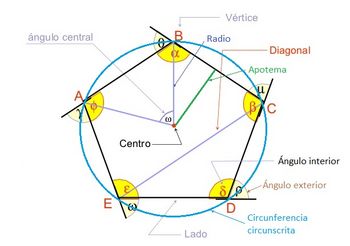
| ===Elementos de un polígono regular=== | ===Elementos de un polígono regular=== | ||
| Línea 27: | Línea 33: | ||
| |descripcion=Actividades en las que podrás aprender el concepto de polígono regular y a identificar sus elementos. | |descripcion=Actividades en las que podrás aprender el concepto de polígono regular y a identificar sus elementos. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena9/1quincena9_contenidos_4a.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena9/1quincena9_contenidos_4a.htm | ||
| + | }} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Circunferencia circunscrita y apotema | ||
| + | |descripcion=Actividades sobre la circunferencia circunscrita y la apotema de los polígonos regulares. | ||
| + | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/Poligonos_regulares_y_circulos/Polici2.htm | ||
| }} | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| Línea 40: | Línea 51: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Tabla75|celda2=[[Imagen:Apotema.png|center|300px]]|celda1= | + | {{Tabla75|celda2=[[Imagen:Apotema.png|center|350px]]|celda1= |
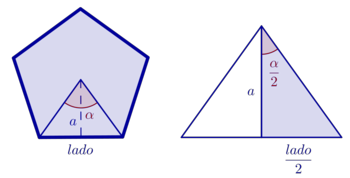
| {{Teorema|titulo=Propiedades|enunciado=*Dos radios consecutivos forman un triángulo isósceles con uno de los lados del polígono regular, siendo su altura la apotema. | {{Teorema|titulo=Propiedades|enunciado=*Dos radios consecutivos forman un triángulo isósceles con uno de los lados del polígono regular, siendo su altura la apotema. | ||
| - | *En el caso del hexágono regular este triángulo es equilátero.|demo= Las demostraciones son inmediatas ya que si el triángulo está formado por dos radios, necesariamente es isósceles. En el caso del hexágono este triángulo es equilátero porque su ángulo central mide 60º, como podrá verse en la propiedad del siguiente apartado que habla sobre ángulos centrales.}} | + | *La apotema divide al triángulo en dos mitades iguales que son triángulos rectángulos. |
| + | *En el caso del hexágono regular este triángulo es equilátero. | ||
| + | *Todo polígono regular se puede inscribir en una circunferencia que se llama '''circunferencia circunscrita''', cuyo centro y radio son el centro y el radio del polígono. | ||
| + | |demo= Las demostraciones son inmediatas. En efecto: | ||
| + | *Si el triángulo está formado por dos radios, necesariamente es isósceles. | ||
| + | |||
| + | *En el caso del hexágono este triángulo es equilátero porque su ángulo central mide 60º, como podrá verse en la propiedad del siguiente apartado que habla sobre ángulos centrales. | ||
| + | |||
| + | *Como la apotema une el centro con el punto medio del lado y el triángulo es isósceles, lo divide en dos mitades iguales. Al se iguales, el ángulo que forma la apotema con el lado ha de ser necesariamente de 90º, que es la mitad de un ángulo llano. | ||
| + | |||
| + | *Teniendo en cuenta que todos los radios unen el centro con los vértices, podemos trazar una circunferencia que pase por todos ellos y por tanto el polígono queda inscrito en ella.}} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 51: | Línea 72: | ||
| {{Teorema|titulo=Propiedad: ''Ángulos centrales''|enunciado=El ángulo central de un polígono regular mide lo mismo que el ángulo exterior y esta medida es <math>\cfrac{360^\circ}{n}</math>.|demo=Es inmediata, ya que un polígono regular de ''n'' lados tiene ''n'' ángulos centrales iguales y entre todos suman 360º}} | {{Teorema|titulo=Propiedad: ''Ángulos centrales''|enunciado=El ángulo central de un polígono regular mide lo mismo que el ángulo exterior y esta medida es <math>\cfrac{360^\circ}{n}</math>.|demo=Es inmediata, ya que un polígono regular de ''n'' lados tiene ''n'' ángulos centrales iguales y entre todos suman 360º}} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_estudiia | ||
| + | |titulo1=Ángulo central de un polígono regular | ||
| + | |duracion=2´28" | ||
| + | |url1=https://youtu.be/mK__a67K-Eo | ||
| + | |sinopsis=Cálculo del ángulo central de un polígono regular. Ejemplo. | ||
| + | }} | ||
| + | {{Video_enlace_velazco | ||
| + | |titulo1=Ángulo central de un polígono regular | ||
| + | |duracion=1´12" | ||
| + | |url1=https://www.youtube.com/watch?v=lVhAU17Ggr0 | ||
| + | |sinopsis=Cálculo del ángulo central de un polígono regular. Ejemplo. | ||
| + | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver los ángulos central, interior y exterior de un polígono regular de hasta 20 lados. | |descripcion=En esta escena podrás ver los ángulos central, interior y exterior de un polígono regular de hasta 20 lados. | ||
| Línea 79: | Línea 112: | ||
| {{p}} | {{p}} | ||
| ==Construcciones con regla y compás== | ==Construcciones con regla y compás== | ||
| + | {{AI_anaya | ||
| + | |titulo1=Construcciones del pentágono y del octógono regular | ||
| + | |descripcion= | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://www.edistribucion.es/anayaeducacion/8420033/flash/ud12/12_5.html | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |url1=http://www.edistribucion.es/anayaeducacion/8420033/flash/ud12/12_5.html | ||
| + | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=Polígonos regulares inscritos en la circunferencia | |titulo1=Polígonos regulares inscritos en la circunferencia | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Polígono regular
Un polígono regular es aquel cuyos lados tienen la misma longitud y cuyos ángulos son iguales.
Actividad sobre polígonos regulares.
Elementos de un polígono regular
Actividades en las que podrás aprender el concepto de polígono regular y a identificar sus elementos. Actividades sobre la circunferencia circunscrita y la apotema de los polígonos regulares. En esta escena podrás ver los elementos de un polígono regular. Concepto de polígono regular y ejemplos. Elementos de un polígono regular. |
Propiedades
Demostración: Las demostraciones son inmediatas. En efecto:
|
Medida de los ángulos de un polígono regular
Propiedades
- La suma de los ángulos interiores de un polígono de
 lados es igual a
lados es igual a 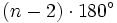 .
.
- Si el polígono de
 lados es regular:
lados es regular:
- Cada ángulo interior mide
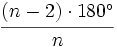 .
.
- Cada ángulo exterior mide
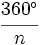 .
.
- Cada ángulo interior mide
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
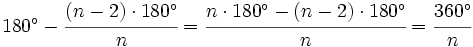
- Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular.
Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Suma de los ángulos interiores de un polígono.
- Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de su suma.
Ángulos interiores de un cuadrado y de un hexágono regular.
¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulo exterior de un polígono regular
Propiedad: Ángulos centrales
El ángulo central de un polígono regular mide lo mismo que el ángulo exterior y esta medida es 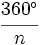 .
.
Es inmediata, ya que un polígono regular de n lados tiene n ángulos centrales iguales y entre todos suman 360º
Cálculo del ángulo central de un polígono regular. Ejemplo.
Cálculo del ángulo central de un polígono regular. Ejemplo.
En esta escena podrás ver los ángulos central, interior y exterior de un polígono regular de hasta 20 lados.
Actividades en las que podrás aprender a calcular la medida de los ángulos interiores, centrales y exteriores de un polígono regular.
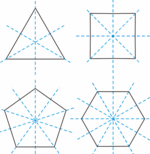
Ejes de simetría de los polígonos regulares
|
Actividades en las que podrás aprender a averiguar los ejes de simetría de un polígono regular. ¿Qué es un eje de simetría?. Ejes de simetría en los polígonos regulares. |
Construcciones con regla y compás
Construcción de polígonos regulares inscritos en una circunferencia, con regla y compás.
Construcción de polígonos regulares conocido el lado, con regla y compás.