Contrastes de hipótesis sobre medias y proporciones

De Wikipedia

Revisión de 10:41 11 jul 2007 Juanmf (Discusión | contribuciones) (→Introducción) ← Ir a diferencia anterior		Revisión de 10:47 11 jul 2007 Juanmf (Discusión | contribuciones) (→Introducción) Ir a siguiente diferencia →
Línea 31:		Línea 31:
	Si la duración media <math> \bar{X} </math> en la muestra de las 25 bombillas está en la zona de aceptación, aceptamos la hipótesis nula, en caso contrario la rechazamos.		Si la duración media <math> \bar{X} </math> en la muestra de las 25 bombillas está en la zona de aceptación, aceptamos la hipótesis nula, en caso contrario la rechazamos.
-	En general, la hipótesis nula <math>(H_0) </math> afirma algo sobre el valor de un parámetro de una población cuya verdad se quiere probar. Se llama '''test''' a un procedimiento que permita pronunciarse a favor o en contra de dicha hipótesis, en el transcurso de una experiencia aleatoria	+	En general, la hipótesis nula <math>(H_0) </math> afirma algo sobre el valor de un parámetro de una población cuya verdad se quiere probar. Se llama '''test''' a un procedimiento que permita pronunciarse a favor o en contra de dicha hipótesis, frente a otra <math>(H_1)</math> llamada '''hipótesis alternativa''', en el transcurso de una experiencia aleatoria

---

Revisión de 10:47 11 jul 2007

Tabla de contenidos 1 Introducción

Introducción

Empezaremos con un ejemplo del tipo de problema que queremos resolver:

Supongamos que se fabrican bombillas que tienen una duración normal X y una desviación tipica σ = 0.5. El fabricante afirma que la duración media de las bombillas es de μ = 5 meses.

Para contrastar esta afirmación se estudia una muestra de n = 25 bombillas y se halla la duración media 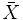de las 25 bombillas. Queremos ver si es cierto lo que afirma que lo llamaremos Hipótesis nula (H₀).

El estadístico 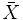se distribuye:

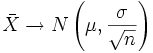
Luego si fijamos un nivel de confianza 1 − α = 0.95 el valor de 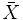estará en el intervalo

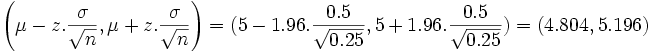
con una probabilidad de 0.95.

A este intervalo se le llama zona de aceptación.

Si la duración media 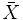en la muestra de las 25 bombillas está en la zona de aceptación, aceptamos la hipótesis nula, en caso contrario la rechazamos.

En general, la hipótesis nula (H₀) afirma algo sobre el valor de un parámetro de una población cuya verdad se quiere probar. Se llama test a un procedimiento que permita pronunciarse a favor o en contra de dicha hipótesis, frente a otra (H₁) llamada hipótesis alternativa, en el transcurso de una experiencia aleatoria