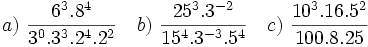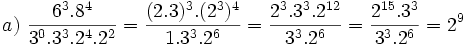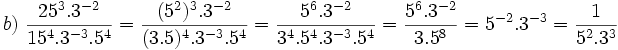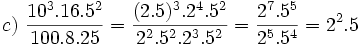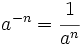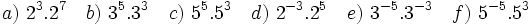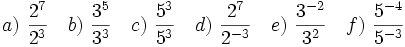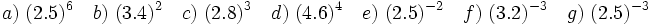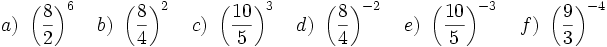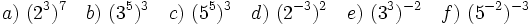Números racionales: Potencias
De Wikipedia
| Revisión de 11:26 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:28 7 ago 2007 Coordinador (Discusión | contribuciones) (→Potenciación de fracciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Potenciación de fracciones=== | + | ==Potenciación de fracciones== |
| Las potencias con números racionales cumplen las mismas [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales#Propiedades_de_las_potencias_de_naturales propiedades] que con números naturales y enteros.{{p}} | Las potencias con números racionales cumplen las mismas [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales#Propiedades_de_las_potencias_de_naturales propiedades] que con números naturales y enteros.{{p}} | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido=Pulsa los botones para obtener ejemplos de cada tipo:{{p}} | {{Desplegable|titulo=Ejemplos:{{b}}|contenido=Pulsa los botones para obtener ejemplos de cada tipo:{{p}} | ||
| Línea 25: | Línea 25: | ||
| {{p}} | {{p}} | ||
| Tan sólo queda añadir el siguiente caso: | Tan sólo queda añadir el siguiente caso: | ||
| - | ====Potencias de exponente negativo==== | + | ===Potencias de exponente negativo=== |
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
| Sea <math>n \in \mathbb{N}</math>, se define la potencia de exponente negativo como: | Sea <math>n \in \mathbb{N}</math>, se define la potencia de exponente negativo como: | ||
| Línea 172: | Línea 172: | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| ==Ejercicios== | ==Ejercicios== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 11:28 7 ago 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Potenciación de fracciones
Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros.Pulsa los botones para obtener ejemplos de cada tipo:
Tan sólo queda añadir el siguiente caso:
Potencias de exponente negativo
Sea 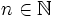 , se define la potencia de exponente negativo como:
, se define la potencia de exponente negativo como:
|
|
Como consecuencia, 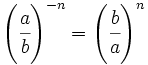 .
.
|
Actividad Interactiva: Potencias de exponente negativo
Actividad 1. Potencias de exponente negativo.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) 3 − 5 b) 5 − 3 c) 7 − 2 d) 2 − 7 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Actividad 2. Autoevaluación.
Actividad: Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien. |
|
Actividad Interactiva: Potencias de racionales
Actividad 1. Autoevaluación: Operaciones con potencias de racionales.
Actividad: Pulsa el botón EJERCICIO para ver el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena (de forma que la base no sea una potencia) y pulsas el botón SOLUCIÓN para ver si lo has hecho bien. |
|
Actividades Interactivas:Potencias
Actividad 1: Producto de potencias.
Actividad: Escribe en tu cuaderno los siguientes productos en forma de potencia:
Actividad 2: Cociente de potencias.
Actividad: Escribe en tu cuaderno los siguientes cocientes en forma de potencia:
Actividad 3: Potencia de un producto.
Actividad: Expresa en forma de producto de potencias los siguientes expresiones:
Actividad 4: Potencia de un cociente.
Actividad: Expresa en forma de cociente de potencias los siguientes expresiones:
Actividad 5: Potencia de una potencia.
Actividad: Escribe en tu cuaderno las siguientes potencias en forma de potencia con un solo exponente:
|
Ejercicios
{{ejercicio |titulo=Ejercicios: |cuerpo=
1. Simplifica y expresa en forma de fracción:
- a)
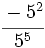 b)
b) 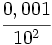 c)
c) 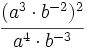
a)
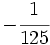 b)
b) 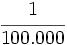 c)
c) 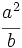
2. Simplifica:
- a)
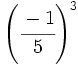 b)
b) ![\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2](/wikipedia/images/math/1/4/e/14e6c8e9222f905775e21fb947d71f2c.png) c)
c) 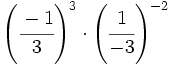
a)
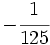 b)
b) 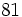 c)
c) 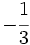
3. Calcula utilizando las propiedades de las potencias: