Funciones: Definición
De Wikipedia
| Revisión de 11:25 21 abr 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:26 21 abr 2008 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| |ampliar= | |ampliar= | ||
| [http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/3eso/solucionlibro/unidad10.pdf Ejercicios 1]<br>[http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/3eso/funciones/teoriainterpretaciondegraficas/teoriainterpretaciondegraficas.htm Ejercicios 2] | [http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/3eso/solucionlibro/unidad10.pdf Ejercicios 1]<br>[http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/materiales/3eso/funciones/teoriainterpretaciondegraficas/teoriainterpretaciondegraficas.htm Ejercicios 2] | ||
| - | |repasar=[http://maralboran.org/web_ma/descartes/3_eso/Coordenadas_cartesianas/index.htm Coordenadas]<br>[http://www.librosvivos.net/smtc/homeTC.asp?TemaClave=1067 SM] | + | |repasar=[http://maralboran.org/web_ma/descartes/3_eso/Coordenadas_cartesianas/index.htm Coordenadas]<br>[http://www.librosvivos.net/smtc/homeTC.asp?TemaClave=1067 Funciones (SM)] |
| |enlaces=[http://es.wikipedia.org/wiki/Funci%C3%B3n_%28matem%C3%A1tica%29 Función]<br>[http://es.wikipedia.org/wiki/Lista_de_funciones Lista de funciones] | |enlaces=[http://es.wikipedia.org/wiki/Funci%C3%B3n_%28matem%C3%A1tica%29 Función]<br>[http://es.wikipedia.org/wiki/Lista_de_funciones Lista de funciones] | ||
| }} | }} | ||
Revisión de 11:26 21 abr 2008
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Coordenadas Funciones (SM) | Ejercicios 1 Ejercicios 2 | WIRIS Geogebra Calculadora Función Lista de funciones |
Definición
Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente x, le asocia un único valor de la variable dependiente y, que llamaremos imagen de x. Decimos que y es función de x y lo representamos por
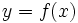
Formas de expresar una función
Hay varias formas de expresar una función:
- Mediante un enunciado.
- Mediante una expresión algebraica.
- Mediante una gráfica.
Veamos unos ejemplos en la siguiente actividad:
|
Actividades Interactivas: Formas de expresar una función
1. Un ejemplo en el que la variable independiente es discreta.
Actividad:
El precio de un bolígrafo en la papelería cercana es de 0,30 €.
Para calcular el precio de un número x de bolígrafos, multiplicaremos la variable independiente x por 0,30. El valor obtenido se le asigna a la variable dependiente y. 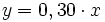
Esta tabla se llama tabla de valores. a) Calcula y escribe los valores que faltan en la tabla.
Para representar gráficamente una función utilizamos unos ejes cartesianos con una escala adecuada. Sobre el eje horizontal (eje de abscisas) representamos la variable independiente x, y sobre el eje vertical (eje de ordenadas) la variable dependiente y. Cada punto de la gráfica es generado por una pareja de valores x e y, que son sus coordenadas (x,y), su abcisa y su ordenada. En la escena siguiente hemos dibujado unos ejes coordenados. En el eje horizontal representamos el número de bolígrafos que compramos. En el eje vertical representamos el precio de la compra. Para cada valor que le asignes al número de bolígrafos se marca en su vertical el precio de esos bolígrafos con un punto rojo. En la parte inferior de la escena asígnale a la variable bolígrafos los valores de la tabla anterior y observa su precio, es decir, la altura donde se coloca el punto rojo. b) ¿Qué mide un cuadradito cualquiera del eje horizontal? c) ¿Qué mide un cuadradito cualquiera del eje vertical? d) Fijándote en la gráfica, ¿cuánto cuestan 16 bolígrafos? ¿Cuántos bolígrafos te dan por 3,60 €? e) ¿Tiene sentido unir los puntos rojos de la gráfica? ¿Por qué?
2. Un caso en el que la variable independiente es continua.
Actividad: El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas. Pero hay una importante diferencia entre ambos ejemplos: no podemos comprar fracciones de bolígrafos (1,5 o 2,7 bolígrafos) y en cambio sí podemos comprar fracciones de kilos de patatas (1,5 o 2,7 kilos de patatas). a) Calcula y anota los precios de las siguientes cantidades de patatas. Asígnale esos valores a la variable kilos de la escena siguiente.
b) ¿Tiene sentido ahora unir los puntos rojos de la gráfica? Compuébalo en la escena asignándole a la variable kilos el valor 0 y a continuación, mantén pulsado el botón del ratón sobre la fecha superior de los kilos de patatas. En el primer caso, la gráfica estaba formada por puntos aislados. En este segundo caso, la gráfica es una curva (en este caso, una recta) continua. |
En la actividad anterior hemos podido ver que la variable independiente puede ser:
- Discreta: Si los valores que toma van dando saltos. Su gráfica está formada por puntos separados. Por ejemplo, la variable "número de boligrafos que compramos en una papelería".
- Continua: Si los valores que toma no dan saltos. Su gráfica está formada por trazos. Por ejemplo, la variable "peso de una persona".
|
Actividades Interactivas: Interpretación de gráficas
1. Determina si son o no son funciones las siguientes gráficas.
Actividad: Una función es una relación entre dos variables numéricas, habitualmente las denominamos x (variable independiente) e y (variable dependiente); Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente. Pero además, para que una relación sea función, a cada valor de la variable independiente le corresponde uno y sólo un valor de la variable dependiente, no le pueden corresponder dos o más valores. a) Observa en la escena las gráficas y di cuál de ellas es función y por qué no lo es la otra. Observa al mover el punto P cuántos puntos de corte tiene la recta azul con cada gráfica; si es más de uno no es una función.
2. Función cuya gráfica es una recta.
Actividad: La siguiente escena representa una botella (en color rojo) que cuando abras el grifo se comenzará a llenar de agua. El proceso de llenado de la botella se puede describir matemáticamente con lo que llamamos función, así para un tiempo concreto la función nos dice la altura de la botella en ese momento. El dibujo que queda tras el punto A se llama gráfica de la función. Haz clic en el botón y dejándolo pulsado observa cómo se llena la botella . Observa que en el eje horizontal representamos el tiempo que dejamos el grifo abierto y en el vertical la altura que el agua alcanza en la botella. En el eje horizontal hemos empezado a marcar 1 segundo, 2 segundos, etc. Observa en este ejemplo, que la altura es cero cuando el tiempo transcurrido es cero y que la gráfica va creciendo. a) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas. Si haces clic sobre un punto con el cursor te aparecerán los valores horizontal (tiempo) y vertical (altura) para ese punto. b) ¿Qué puedes decir de la relación entre las variables tiempo y altura? c) ¿Cuánto tiempo necesita la botella para llenarse hasta la mitad? d) ¿Cuánto tiempo necesita la botella para llenarse un cuarto? ¿Y tres cuartos?
3. Función cuya gráfica no es una recta.
Actividad: En la siguiente escena la forma de la botella ha cambiado. a) Intenta hacer la gráfica antes de ver como queda en la escena. b) Observa las alturas que se alcanzan cuando han transcurrido 2, 4 y 6 segundos. Anótalas. c) ¿Qué puedes decir de la relación entre las alturas y los tiempos? d) Ahora la altura del agua según pasa el tiempo sube más despacio, ¿por qué? Ahora prueba a cambiar la forma de la botella moviendo el punto P. e) Haz una botella con la boca más estrecha que la base y observa las distintas gráficas que se generan. Da una explicación de lo qué ocurre. f) Las gráficas unas veces son convexas (tipo U) y otras cóncavas (tipo U invertida), ¿de qué depende? |
Ejercicios
|
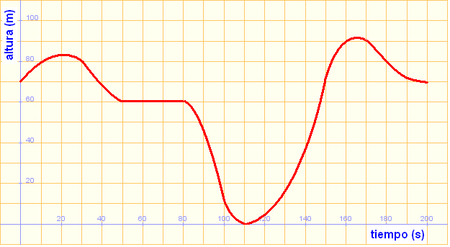
Ejercicio: Funciones y gráficas 1. La siguiente gráfica describe el vuelo de un águila desde que sale del nido hasta que vuelve a él con una presa que caza durante el trayecto.
Solución:
2. Poner una anuncio por palabras cuesta una cantidad fija de 0.50 € y 0.05 € por cada palabra.
|
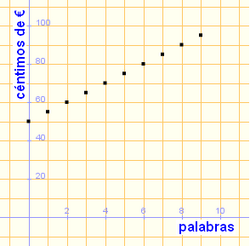
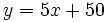 (céntimos de €)
(céntimos de €)
