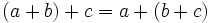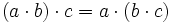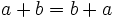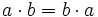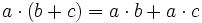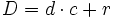Números Naturales (4ºESO-A)
De Wikipedia
| Revisión de 11:38 27 may 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Algoritmo de la división) |
||
| Línea 1: | Línea 1: | ||
| {{Menú Matemáticas 4ESOA | {{Menú Matemáticas 4ESOA | ||
| |ir= |ampliar= | |ir= |ampliar= | ||
| - | |repasar= | + | |repasar=[[Números naturales: Operaciones | Operaciones. Sacar factor común]]<br>[[Números naturales: Potencias | Potencias]]<br>[[Números naturales: Jerarquía de las operaciones | Jerarquía de las operaciones]]<br>[[Números naturales: Calculadora | Calculadora]] |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| Línea 61: | Línea 61: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejercicio | + | |
| - | |titulo=Problema: ''División con naturales'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''1. '''Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor? | + | |
| - | |sol= | + | |
| - | El divisor es 14 (Aplicando la regla de la división) | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| ==Jerarquía de las operaciones== | ==Jerarquía de las operaciones== | ||
| A la hora de operar con números naturales seguiremos las siguientes pautas: | A la hora de operar con números naturales seguiremos las siguientes pautas: | ||
| Línea 77: | Línea 67: | ||
| Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Jerarquía de las operaciones''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Operaciones combinadas. | ||
| - | |actividad= | ||
| - | En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. | ||
| - | Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. | ||
| - | |||
| - | Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/naturales2/opcombin_1.html | ||
| - | width=450 | ||
| - | height=350 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| ==Potenciación de naturales== | ==Potenciación de naturales== | ||
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones. Sacar factor común Potencias Jerarquía de las operaciones Calculadora | WIRIS Calculadora |
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
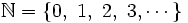
Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Video: Números naturales. Números primos (17´)
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.
Representación de los números naturales
Podemos representarlos en una recta:
Suma y multiplicación de naturales
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Propiedades de la suma y el producto de naturales
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
División con naturales
La división puede verse como un reparto de un número de elementos (dividendo) en un número de partes iguales (divisor), que da como resultado el número de elementos que corresponden a cada parte (cociente) y un posible número de elementos sobrantes (resto). Si el resto es cero la división se llama exacta, si no, se llama entera.
Algoritmo de la división
Algoritmo de la división
- En toda división, el dividendo es igual al divisor por el cociente más el resto.
|
|
- donde
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
Jerarquía de las operaciones
A la hora de operar con números naturales seguiremos las siguientes pautas:
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
Potenciación de naturales
Una potencia de base  y exponente
y exponente  consiste en multiplicar
consiste en multiplicar  veces la base
veces la base  .
.
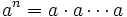
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo.
En la expresión de la potencia de un número consideramos dos partes:
- La base es el número que se multiplica por sí mismo
- El exponente es el número que indica las veces que la base aparece como factor.