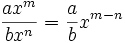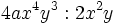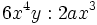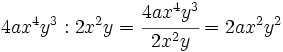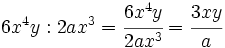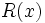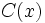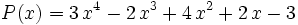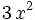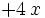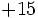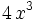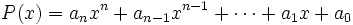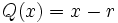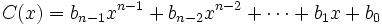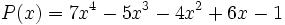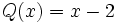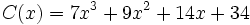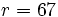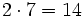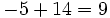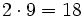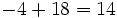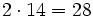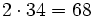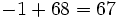Regla de Ruffini (4ºESO Académicas)

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 12:27 14 ene 2009

Menú: [Mostrar]

Tabla de contenidos

[esconder]

1 Cociente de monomios
2 División de polinomios
- 2.1 División de un polinomio por (x-a). Regla de Ruffini

Cociente de monomios

Entenderemos la división de monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.

$\frac{ax^m} {bx^n}= \frac{a} {b} x^{m-n}$

Ejemplos: Cociente de monomios

Calcula:

a) $4ax^4y^3 : 2x^2y \;\!$

b) $6x^4y : 2ax^3 \;\!$

Solución:[Mostrar]

División de polinomios

La división polinómica es, en ciertos aspectos, similar a la división numérica.

Dados dos polinomios $P(x)\;$ (dividendo) y $Q(x)\;$ (divisor) de modo que el grado de $P(x)\;$ sea mayor o igual que el grado de $Q(x)\;$ y el grado de $Q(x)\;$ sea mayor o igual a cero, siempre podremos hallar dos polinomios 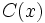$C(x)\;$ (cocient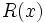e) y $R(x)\;$ (resto) tales que:

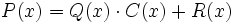
$P(x) = Q(x) \cdot C(x)+ R(x) \,$

dividendo = divisor × cociente + resto

que también podemos representar como:

$P(x) \,$		$Q(x) \,$
$R(x) \,$		$C(x) \,$

El grado de C(x) está determinado por la diferencia entre los grados de P(x) y Q(x), mientras que el grado de R(x) será, como máximo, un grado menor que Q(x).
Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.

Ejemplo: División de polinomios

Divide los siguientes polinomios:

$P(x) = 3 \, x^{4} - 2 \, x^{3} + 4 \, x^{2} + 2 \, x - 3\;$

$Q(x) = x^{2} - 2 \, x - 1 \;$

Solución:[Mostrar]

División de un polinomio por (x-a). Regla de Ruffini

Regla de Ruffini

La Regla de Ruffini nos permite dividir un polinomio entre un binomio de la forma 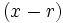$(x-r)\;$ , siendo $r\;$ un número entero.

Debemos esta regla al matemático italiano Paolo Ruffini,

Demostración:[Mostrar]

Vamos a dividir el polinomio

$P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$

entre el binomio

$Q(x)=x-r\,\!$

para obtener el cociente

$C(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1x+b_0$

y el resto 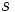$s\;$ .

1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de $P(x)\;$ y los escribimos ordenados. Entonces escribimos r en la parte inferior izquierda del eje, encima de la línea:

    |        a_n        a_n-1       ...        a₁         a₀
    |                                    
 r  |                                    
----|---------------------------------------------------------
    |                                    
    |

2. Pasamos el coeficiente más pegado a la izquierda (a_n) abajo, justo debajo de la línea para obtener el primero de los coeficientes b:

    |        a_n        a_n-1       ...        a₁         a₀
    |                                    
  r |                                    
----|---------------------------------------------------------
    |        a_n                     
    |
    |      = b_n-1                                
    |

3. Multiplicamos el número más pegado a la derecha debajo de la línea por r y lo escribimos sobre la línea en la primera posición de la derecha:

    |        a_n        a_n-1       ...        a₁         a₀
    |
  r |                  b_n-1r
----|---------------------------------------------------------
    |        a_n
    |
    |      = b_n-1                                
    |

4. Añadimos los dos valores que hemos puesto en la misma columna:

    |        a_n        a_n-1       ...        a₁         a₀
    |
  r |                  b_n-1r
----|---------------------------------------------------------
    |        a_n     a_n-1+(b_n-1r)
    |
    |      = b_n-1     = b_n-2                                
    |

5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:

    |        a_n        a_n-1       ...        a₁         a₀
    |
  r |                  b_n-1r      ...        b₁r        b₀r
----|---------------------------------------------------------
    |        a_n     a_n-1+(b_n-1r)  ...       a₁+b₁r       a₀+b₀r
    |
    |      = b_n-1     = b_n-2      ...       = b₀        = s
    |

Los valores 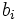$b_i\;$ son los coeficientes del polinomio resultante 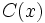$C(x)\;$ , el grado será menor que el grado de $P(x)\;$ . El resto será $s\;$ .

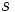Ejemplo: Regla de Ruffini

Divide los polinomios usando la regla de Ruffini:

$P(x)=7x^4-5x^3-4x^2+6x-1\,\!$

$Q(x)=x-2\,\!$

Solución:[Mostrar]

Obtenido de "http://maralboran.org/wikipedia/index.php/Regla_de_Ruffini_%284%C2%BAESO_Acad%C3%A9micas%29"

Categorías: Matemáticas | Álgebra

 Vamos a dividir el polinomio
-<center><math>P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0</math></center>
+:<math>P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0</math>
 entre el binomio
-<center><math>Q(x)=x-r\,\!</math></center>
+:<math>Q(x)=x-r\,\!</math>
 para obtener el cociente
-<center><math>C(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1x+b_0</math></center>
+:<math>C(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1x+b_0</math>
 y el resto <math>s\;</math>.
-. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de ''P''(''x'') y los escribimos ordenados. Entonces escribimos ''r'' en la parte inferior izquierda del eje, encima de la línea:
+. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de <math>P(x)\;</math> y los escribimos ordenados. Entonces escribimos ''r'' en la parte inferior izquierda del eje, encima de la línea:
      |        a<sub>n</sub>        a<sub>n-1</sub>       ...        a<sub>1</sub>         a<sub>0</sub>

Enlaces internos	Para repasar	Enlaces externos
Indice Descartes Manual Casio	Test de Álgebra	WIRIS Calculadora

$3 \, x^{4} \;$	$- 2 \, x^{3} \;$	$+ 4 \, x^{2} \;$	$+ 2 \, x \;$	$- 3 \;$	$x^{2} \;$	$- 2 \, x \;$	$- 1 \;$
$- 3 \, x^{4} \;$	$+ 6 \, x^{3} \;$	$+ 3 \, x^{2} \;$			$3 \, x^{2} \;$	$+ 4 \, x \;$	$+ 15 \;$
	$4 \, x^{3} \;$	$+ 7 \, x^{2} \;$	$+ 2 \, x \;$	$- 3 \;$
	$- 4 \, x^{3} \;$	$+ 8 \, x^{2} \;$	$+ 4 \, x \;$
		$15 \, x^{2} \;$	$+ 6 \, x \;$	$- 3 \;$
		$- 15 \, x^{2} \;$	$+ 30 \, x \;$	$+ 15 \;$
			$36 \, x \;$	$+ 12 \;$

Regla de Ruffini (4ºESO Académicas)

De Wikipedia

Revisión de 12:27 14 ene 2009

Tabla de contenidos

Cociente de monomios

División de polinomios

División de un polinomio por (x-a). Regla de Ruffini

Vistas

Herramientas personales

Menú

Buscar

Herramientas