Plantilla:Factorización de polinomios de grado 2

(Diferencia entre revisiones)

Revisión de 17:01 15 ago 2016

Factorización de polinomios de segundo grado

Un polinomio de segundo grado, 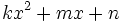$kx^2+mx+n\;$ , con raíces rales, $a\;$ y $b\;$ , se puede factorizar de la forma

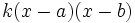
$k(x-a)(x-b)\;$

Ejemplos: Factorización de polinomios de segundo grado y reducibles

Factoriza los siguientes polinomios

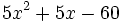
a) $5x^2+5x-60\;$

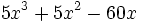
b) $5x^3+5x^2-60x\;$

Solución:

El polinomio 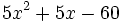$5x^2+5x-60\;$ tiene dos raíces: 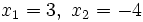$x_1=3,\ x_2=-4$ , que se obtienen de resolver la ecuación de segundo grado 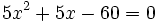$5x^2+5x-60=0\;$ . Entonces:

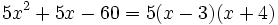
$5x^2+5x-60=5(x-3)(x+4)\;$

El polinomio incompleto de grado 3, 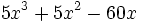$5x^3+5x^2-60x\;$ , se puede descomponer de la siguiente manera:

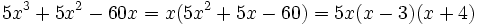
$5x^3+5x^2-60x=x(5x^2+5x-60)=5x(x-3)(x+4)\;$

(Observa que primero hemos sacado factor común $x\;$ y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).

-{{Teorema|titulo=''Factorización de polinomios de segundo grado''
+{{Teorema_sin_demo|titulo=''Factorización de polinomios de segundo grado''
 |enunciado=
-Un polinomio de segundo grado, <math>kx^2+mx+n\;</math>, con raíces rales, <math>a\;</math> y <math>b\;</math>, se puede factorizar de la forma
+:Un polinomio de segundo grado, <math>kx^2+mx+n\;</math>, con raíces rales, <math>a\;</math> y <math>b\;</math>, se puede factorizar de la forma
 {{p}}
 <center><math>k(x-a)(x-b)\;</math></center>
 {{p}}
 {{ejemplo|titulo=Ejemplos: ''Factorización de polinomios de segundo grado y reducibles''
-|enunciado= Factoriza los siguientes polinomios
+|enunciado=
+:Factoriza los siguientes polinomios
 ::a) <math>5x^2+5x-60\;</math>
 ::b) <math>5x^3+5x^2-60x\;</math>