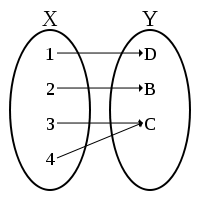
Función sobreyectiva
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:13 24 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 10: | Línea 10: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Función inyectiva'' | + | {{Ejemplo|titulo=Ejemplo: ''Función sobreyectiva'' |
| |enunciado= | |enunciado= | ||
| - | La función <math>f:\mathbb{R}\to\mathbb{R}^+</math>, dada por <math>f(x)=x^2\,</math> es suprayectiva. | + | La función <math>f:\mathbb{R}\to\mathbb{R}^+</math>, dada por <math>f(x)=x^2\,</math> es sobreyectiva. |
| |sol= | |sol= | ||
| En efecto, dado cualquier valor <math>y_0 \in \mathbb{R}^+</math>, existe el valor <math>x=\sqrt{y_0}</math> que se corresponde con él. | En efecto, dado cualquier valor <math>y_0 \in \mathbb{R}^+</math>, existe el valor <math>x=\sqrt{y_0}</math> que se corresponde con él. | ||
Revisión actual
Una función 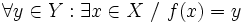 Es decir, una función |
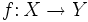 es sobreyectiva, suprayectiva o exhaustiva si todo valor de
es sobreyectiva, suprayectiva o exhaustiva si todo valor de 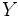 se corresponde con un valor de
se corresponde con un valor de 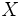 . Simbólicamente:
. Simbólicamente:
 es sobreyectivasi
es sobreyectivasi 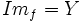
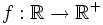 , dada por
, dada por 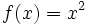 es sobreyectiva.
es sobreyectiva.
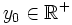 , existe el valor
, existe el valor 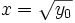 que se corresponde con él.
que se corresponde con él.